Свойства бинарной алгебраической операции
Определение. Операция ◦ на множестве М называется коммутативной, если для любых а и b из этого множества справедливо равенство
a ◦ b = b ◦ a.
Определение. Операция ◦ на множестве М называется ассоциативной, если для любых а, b, c 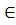 M справедливо равенство
M справедливо равенство
a ◦ (b ◦ c) = (a ◦ b) ◦ c.
Определение. Пусть на М задана операция ◦. Элемент е называется нейтральным относительно операции ◦, если для любого а 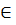 М справедливо равенство
М справедливо равенство
а ◦ е = е ◦ а = а.
Определение. Пусть на М задана операция ◦. Элемент аʹ называется симметричным к элементу а относительно операции ◦, если выполняется равенство
а ◦ аʹ = аʹ ◦ а = е.
По сложению, аʹ обозначают –а и называют противоположным. По умножению, аʹ обозначают 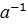 и называют обратным.
и называют обратным.
Определение. Пусть на М задана операция ◦. Операция ◦ называется обратимой, если для любых а, b 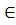 M уравнения а ◦ x = b, y ◦ a = b имеют решение, причем единственное.
M уравнения а ◦ x = b, y ◦ a = b имеют решение, причем единственное.
Пусть дано множество, на котором выполнимы две операции ◦ и *.
Определение. Операция ◦ называется дистрибутивной относительно операции *, если для любых a, b, c 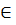 M выполняются равенства
M выполняются равенства
a ◦ (b*c) = (a ◦ b) *(a ◦ c),
(b*c) ◦ a = (b ◦ a) * (c ◦ a).
Пример 1 Докажем, что на множестве R бинарная операция, заданная формулой a ◦ b = 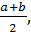 коммутативна, но не ассоциативна.
коммутативна, но не ассоциативна.
Решение. Пусть a, b, c – любые действительные числа. В силу коммутативности сложения на R получим:
a ◦ b = 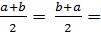 b ◦ a,
b ◦ a,
т.е. бинарная операция нахождения среднего арифметического на R коммутативна. Далее,
(a ◦ b) ◦ c = 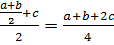 (1)
(1)
и
a ◦ (b ◦ c) = 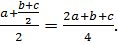 (2)
(2)
Из результатов (1) и (2) следует, что при а ≠ с равенство (a ◦ b) ◦ c=a◦(b ◦ c) не является справедливым. Следовательно, заданная операция не ассоциативна на R.
Пример 2 Докажем, что во множестве К, содержащем не менее двух элементов, на котором формулой a ◦ b = b задана бинарная операция, не существует нейтрального элемента.
Решение
Допустим, что в К существует нейтральный элемент е, и пусть а – любой элемент из К. По определению нейтрального элемента а◦ е = а, а из условия примера следует, что а◦ е = е, т.е. а = е. Это означает, что К состоит из одного элемента. Полученный результат противоречит условию, а потому сделанное допущение ошибочно.
Задачи для решения
1 Являются ли коммутативными и ассоциативными на множестве Z бинарные операции сложения, умножения и вычитания?
2 Докажите, что на множестве 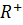 бинарная операция а ◦ b =
бинарная операция а ◦ b = 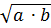 нахождения среднего геометрического коммутативна, но не ассоциативна.
нахождения среднего геометрического коммутативна, но не ассоциативна.
3 Обладает ли множество чисел вида а + b 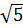 , где a и b – любые целые числа, нейтральным элементом относительно обычного умножения? Проверьте, имеются ли в данной алгебраической системе обратные элементы для элементов 2 +
, где a и b – любые целые числа, нейтральным элементом относительно обычного умножения? Проверьте, имеются ли в данной алгебраической системе обратные элементы для элементов 2 + 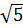 и 5 - 2
и 5 - 2 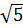 . Обратима ли на данном множестве операция умножения?
. Обратима ли на данном множестве операция умножения?
4 Какие из нижеприведенных бинарных операций:
а) a ◦ b = 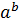 ;
;
б) a ◦ b = c, где с – наибольший общий делитель чисел а и b;
в) a ◦ b = m, где m – наименьшее общее кратное чисел а и b, коммутативны и какие ассоциативны на множестве N.
5 Покажите, что действие выполняемое по правилу a ◦ b = 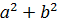 , является коммутативной, но не ассоциативной бинарной операцией на множестве R.
, является коммутативной, но не ассоциативной бинарной операцией на множестве R.
6 Докажите, что относительно обычного умножения множество А={x 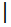 x=3k, k
x=3k, k 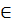 Z} не содержит нейтрального элемента. Обратима ли операция умножения на множестве А?
Z} не содержит нейтрального элемента. Обратима ли операция умножения на множестве А?
7 Пусть I – множество подмножеств некоторого непустого множества М. Существует ли в I нейтральный элемент (если существует, то какой) относительно операции объединения подмножеств на I; пересечения подмножеств? Какие элементы множества I имеют симметричные относительно операций объединения и пересечения? Обратимы ли указанные операции на множестве I?
8 Докажите, что на множестве Q действие, выполняемое по правилу a◦b = = 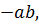 является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система < Z; ◦ > нейтральным элементом, и если обладает, то каким именно?
является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система < Z; ◦ > нейтральным элементом, и если обладает, то каким именно?
Виды алгебр
Определение. Алгеброй называется любое непустое множество А, на котором задана некоторая система операций
S = { 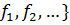
Обозначается (А, S), где А – множество, S – система операций.
Пример. (N, +), (Q, +, ∙)
Определение. Непустое множество М называется полугруппой, если в нем выполнима одна бинарная алгебраическая операция, которая является ассоциативной.
Пример. (N, +), (Z, ∙).
Определение. Непустое множество G называется группой, если в этом множестве выполнима одна бинарная алгебраическая операция ◦, которая обладает свойствами:
1) 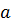 ◦ ( b ◦ c ) = (
◦ ( b ◦ c ) = ( 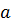 ◦ b ) ◦ c,
◦ b ) ◦ c, 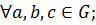
2) 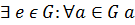 ◦ e = e ◦
◦ e = e ◦ 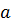 =
= 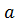 ;
;
3) 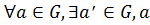 ◦
◦ 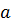 ʹ =
ʹ = 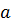 ʹ ◦
ʹ ◦ 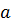 = e.
= e.
Группы по сложению называются аддитивными; группы по умножению – мультипликативными.
Определение. Непустое множество G называется группой, если в этом множестве выполнима одна бинарная алгебраическая операция, которая является ассоциативной и обратимой.
Определение. Если в группе G операция коммутативна, то группа G называется абелевой.
Определение. Непустое множество К называется кольцом, если в нем выполнимы две бинарные алгебраические операции – сложение и умножение, удовлетворяющие условиям:
1) 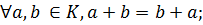
2) 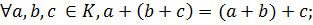
3) 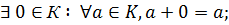
4) 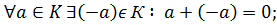
5) 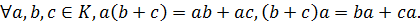
Примеры колец. При обычных операциях сложения и умножения кольцом является множество целых чисел, множество рациональных чисел, множество действительных чисел.
Определение. Непустое множество Р называется полем, если в нем выполнимы две бинарные алгебраические операции сложение и умножение, удовлетворяющие аксиомам:
1) 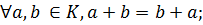
2) 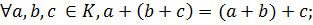
3) 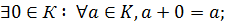
4) 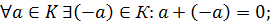
5) 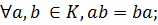
6) 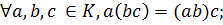
7) 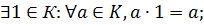
8) 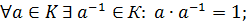
9) 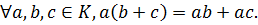
Пример 1 Доказать, что на множество Z образует группу относительно действия, заданного формулой
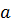 ◦
◦ 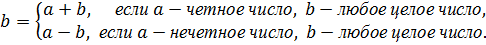
Доказательство
1 Рассматриваемое на Z действие сводится к сложению или вычитанию целых чисел, а т.к. сложение и вычитание элементов из Z дает в результате элемент из Z, то на множестве Z рассматриваемое действие является бинарной операцией.
2 Проанализируем возможные случаи
a) Если a, b – четные числа, а с – любое число из Z, то
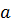 ◦
◦ 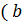 ◦
◦ 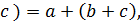
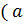 ◦
◦ 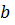 ) ◦
) ◦ 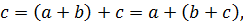
т.е. 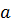 ◦
◦ 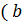 ◦
◦ 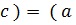 ◦
◦ 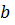 ) ◦
) ◦ 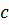 .
.
б) Если a – четное число, b – нечетное, а с – любое число из Z, то
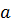 ◦
◦ 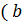 ◦
◦ 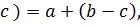
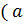 ◦
◦ 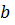 ) ◦
) ◦ 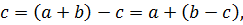
т.е. 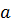 ◦
◦ 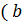 ◦
◦ 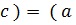 ◦
◦ 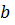 ) ◦
) ◦ 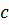 .
.
в) Если a – нечетное число, b – четное, а с – любое число из Z, то 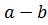 нечетно и потому
нечетно и потому
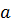 ◦
◦ 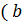 ◦
◦ 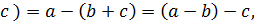
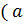 ◦
◦ 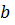 ) ◦
) ◦ 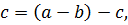
т.е. 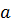 ◦
◦ 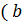 ◦
◦ 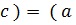 ◦
◦ 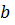 ) ◦
) ◦ 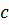 .
.
г) Если a, b – нечетные числа, а с – любое число из Z, то 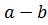 четно и потому
четно и потому
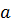 ◦
◦ 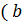 ◦
◦ 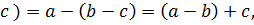
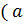 ◦
◦ 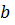 ) ◦
) ◦ 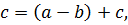
т.е. 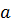 ◦
◦ 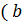 ◦
◦ 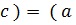 ◦
◦ 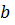 ) ◦
) ◦ 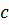 .
.
Итак, во всех возможных случаях заданная на Z бинарная операция является ассоциативной.
3 Т.к. 0 – четное число, то 0 ◦ 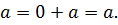 Кроме того, если
Кроме того, если 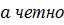 , то
, то 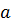 ◦ 0 =
◦ 0 = 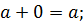 если же
если же 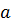 нечетно, то
нечетно, то 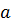 ◦ 0 =
◦ 0 = 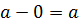 . Итак, 0 ◦
. Итак, 0 ◦ 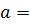
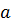 ◦ 0, т.е. 0 является в Z нейтральным элементом относительно заданной операции.
◦ 0, т.е. 0 является в Z нейтральным элементом относительно заданной операции.
4 Для любого элемента 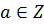 в Z существует обратный элемент: для четного
в Z существует обратный элемент: для четного 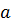 обратным будет противоположное число
обратным будет противоположное число 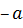 , т.к.
, т.к. 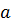 ◦
◦ 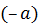 =
= 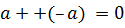 ; для нечетного
; для нечетного 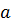 обратным будет само число
обратным будет само число 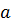 , т.к.
, т.к. 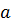 ◦
◦ 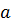 =
= 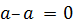 .
.
Итак, Z является группой относительно заданной операции.
Задачи для решения
1 Является ли множество Z полугруппой относительно: а) сложения, б) вычитания?
2 Является ли множество N полугруппой относительно операции нахождения наибольшего общего делителя?
3 Почему множество R не является полугруппой относительно действия, выполняемого по правилу 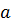 ◦ b =
◦ b = 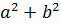 для любых
для любых 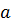 , b
, b 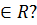
4 Выясните, какие из нижеприведенных множеств являются группами относительно нижеуказанных операций:
а) множество Z относительно вычитания;
б) множество четных чисел относительно умножения;
в) множество целых чисел, кратных любому заданному натуральному числу n, относительно сложения;
г) множество 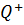 относительно умножения;
относительно умножения;
д) множество Q относительно умножения;
е) множество Q \ {0} относительно умножения;
ж) множество R \ {0} относительно умножения;
з) множество трехмерных (n-мерных) арифметических векторов относительно сложения;
и) множество чисел вида а + b 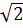 относительно сложения, если а и b – любые рациональные числа;
относительно сложения, если а и b – любые рациональные числа;
к) множество многочленов одной и той же степени n от одного аргумента относительно сложения;
л) множество многочленов степени не выше n относительно сложения;
м) множество многочленов от одного аргумента относительно сложения;
5 На множестве Q 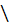 {0} определено действие
{0} определено действие 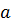 ◦ b =
◦ b = 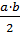 . Докажите, что относительно указанного действия данное множество является группой.
. Докажите, что относительно указанного действия данное множество является группой.
6 Является ли кольцом множество L чисел вида 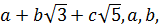
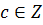 относительно обычных операций сложения и умножения?
относительно обычных операций сложения и умножения?
7 Докажите, что если на Z задана операция a ʘ b = -ab, то алгебраическая система <Z; +, ʘ> является коммутативным кольцом с единицей. Каков единичный элемент этого кольца?
8 Докажите, что множество А чисел вида 2а + 2b 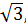 где a, b – любые целые числа, является числовым кольцом.
где a, b – любые целые числа, является числовым кольцом.
9 Для каких чисел n = 2, 3, 4, 5, 6, 7 существует поле из n элементов?
10 Почему кольцо {0} не является полем?
11 На множестве М = {a, b} сложение 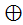 и умножение
и умножение  определены следующим образом:
определены следующим образом:
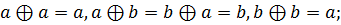
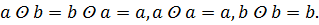
Выясните, обладает ли это множество нулем и единицей и является ли система <M, 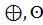 > полем относительно заданных бинарных операций.
> полем относительно заданных бинарных операций.
