Метод сведения дискретной динамической задачи к статической

Одним из возможных методов разработки управленческого решения для динамических задач является метод, основанный на представлении динамической задачи в виде набора самостоятельно существующих статических задач. Пусть рассматривается 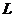дискретных моментов времени. Для каждого из них можно сформулировать самостоятельную задачу разработки управленческого решения (например, однокритериальную статическую в условиях определенности) [1]

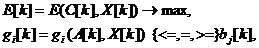
где 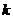- текущий дискретный момент времени, .

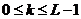Рассмотрим совместную однокритериальную статическую задачу в условиях определенности, решение которой 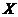представляет собой набор из 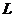самостоятельных решений 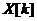для текущего момента времени 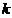. Будем считать, что критериальная функция новой совместной задачи определяется как сумма критериальных функций для каждого момента времени, а ограничения для каждого момента времени добавляются к общему списку ограничений задачи. Тогда условие новой задачи можно записать как

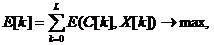
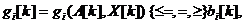
а общее количество уравнений ограничений увеличилось в 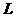раз. Таким образом, решение динамической задачи сводится к решению статической задачи разработки управленческого решения и может осуществляться рассмотренными ранее методами.

Реализация метода в общем случае приводит к существенному росту трудоемкости вычислений. Отметим, что если количество переменных при использовании метода всегда возрастает в 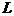раз, то число уравнений ограничений может быть значительно сокращено за счет конкретного рассмотрения динамических параметров. Так, если к категории динамических относятся один или несколько параметров 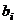, то рассмотрение каждого из них во времени увеличивает количество ограничений в 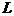раз. Для статических 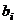нет необходимости увеличивать количество уравнений, поскольку в этом случае они имеют смысл величины имеющегося ресурса на весь интервал планирования. 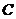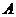Наконец, зависимость от времени неконтролируемых факторов и вообще может быть легко учтена при записи выражения целевой функции или ограничений особенно в численной форме.

Практическая реализация метода сведения динамических задач к статическим может быть осуществлена с использованием современных программных средств, реализующих, например, метод линейного программирования. При выборе используемой программы следует обращать внимание на ограничения программы по максимальному числу переменных и ограничений. Таким образом, метод сведения динамических задач к статическим может быть использован для решения динамических задач разработки управленческого решения.

Лабораторная работа №10. Решение дискретной задачи разработки управленческого решения методом сведения динамической задачи к статической

Задание

Используйте придуманную вами задачу разработки управленческого решения. Переведите ее в категорию динамических дискретных задач и найдите решение, обеспечивающее экстремум критериальной функции задачи, записанной как сумма ее значений для каждого момента времени

Порядок выполнения работы

1. Возьмите в качестве основы решенную вами в процессе выполнения лабораторной работы №2 однокритериальную статическую задачу в условиях определенности.

2. Определите параметр задачи, который будет рассматриваться как зависящий от времени. Согласуйте с преподавателем выбранный вами параметр.

3. Задайтесь количеством интервалов времени 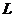, применительно к которым будет решаться задача.

4. Увеличьте общее количество переменных задачи в 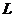раз. Например, при 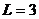для задачи, изображенной на рис. 9, общее количество переменных станет равным 12. Для определенности в обозначения решения введите указание момента времени. Например, обозначение 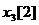означает третий элемент вектора управления, рассматриваемый в момент времени .

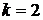5. Задайте значения весовых коэффициентов целевой функции 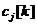для 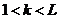. Например, просто скопируйте в соответствующие ячейки рабочего листа значения 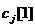, если вы считаете, что они не зависят от времени.

6. Вставьте, если это необходимо, дополнительные строки ограничений для 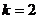, дополнив значениям параметры 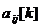при 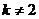. Повторите эти действия для всех остальных возможных значений .

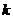7. Запрограммируйте выражения, определяющие расход соответствующего ресурса с учетом увеличения общего числа неизвестных задачи.

8. В соответствующих строках задайте величины ограничений для каждого момента времени .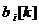

9. Запрограммируйте общее выражение для целевой функции как сумму произведений значений 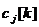на 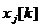и назначьте эту ячейку в качестве целевой в надстройке Поиск решения(рис. 7).

10. В поле Изменяя значения укажите все значения .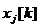

11. В поле Ограничения введите величины израсходованных ресурсов, знаки неравенств и наличие ресурса..

12. Решите задачу поиска оптимального решения и получите оптимальное решение .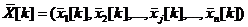

13. Проведите исследование зависимости решения от характера изменения динамического параметра.

Контрольные вопросы

1. Когда задача становится динамической?

2. В чем заключается отличие дискретных задач от непрерывных?

3. Как шаг дискретизации влияет на качество преобразования непрерывного сигнала к дискретному?

4. Как ставятся задачи оптимизации в управлении проектами?

5. Как ставятся задачи оптимизации в теории массового обслуживания?

6. В чем основная идея метода динамического программирования?

7. Как ставятся задачи оптимизации при управлении запасами?

8. Для каких целей можно использовать преобразования Фурье?

9. Чем постановка задачи теории оптимального управления отличается от постановки задачи вариационного исчисления?

10. В чем заключается основная идея метода сведения дискретной динамической задачи к статической?

Отчет о работе

Подготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите динамические параметры, взятые в рассмотрение, и обоснуйте его выбор. Представьте таблицу результатов решения задачи. Сформулируйте выводы, которые можно сделать по результатам выполненной работы.

Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б.

Рациональные решения