Лабораторная работа №6. Решение однокритериальной статической задачи в условиях неопределенности при играх с противником

Задание

Используйте придуманную вами задачу разработки управленческого решения. Задайтесь параметром, который может быть в условиях неопределенности в результате возможных действий противника. Рассматривайте случай дуальной игры с противником с нулевой суммой и решите задачу.

Порядок выполнения работы

1. Из общего числа параметров вашей задачи разработки управленческого решения выберите один, который будет рассматриваться в условиях неопределенности. Согласуйте с преподавателем выбранный вами параметр.

2. На основе анализа ситуации в зависимости от возможных действий противника задайтесь 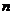возможными значениями случайного параметра 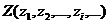, для которых будет делаться расчет. Каждое значение этого параметра будет определять одну из наших стратегий и одну из возможных стратегий противника.

3. Решая задачу с помощью надстройки Поиск решения, определите значение критериальной функции и соответствующие ему решения в предположении, что стратегия противника угадана, то есть мы предполагаем значение параметра 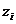, и в результате действий противника он принимает именно такое значение.

4. Постройте платежную матрицу, заполните ее диагональ значениями 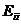и отдельно запишите соответствующие им решения .

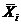5. Используя выражение для показателя эффективности, рассчитайте значения критериальной функции 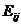в предположении, мы используем стратегию 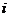, то есть решение 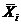, а в результате действий противника параметр принимает значение .

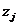6. Заполните значениями 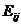свободные клетки платежной матрицы.

7. Просматривая колонки платежной матрицы ( 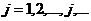), найдите для каждой строки 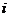наш гарантированный минимальный выигрыш .

8. Найдите номер нашей стратегии, обеспечивающей нам максимум гарантированного выигрыша (нижнюю цену игры) .

9. Просматривая строки платежной матрицы ( 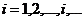), найдите для каждого столбца 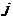гарантированный максимальный проигрыш противника (верхнюю цену игры) .

10. Найдите номер стратегии противника, обеспечивающей ему минимум гарантированного выигрыша .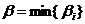

11. Сравните верхнюю и нижнюю цены игры и определите факт наличия или отсутствия седловой точки.

12. Если седловая точка существует ( 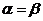), то определите оптимальное решение задачи 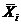соответствующее номеру чистой стратегии, обеспечивающей .

13. Если седловая точка отсутствует ( 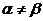), то определите набор 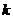своих стратегий 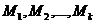, которые обеспечивают значение 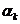, имеют свой выигрыш 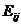и будут чередоваться нами в случайном порядке. Аналогично определите набор 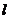стратегий противника 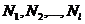. Сформируйте новую матрицу 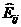размером 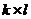, элементы которой представляют выборку из платежной матрицы в соответствии с принятыми в рассмотрение стратегиями.

14. Отдельно сформулируйте и решите еще одну задачу линейного программирования, принимая во внимание 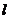ограничений

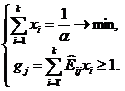
15. В соответствии с полученным решением 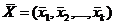по формуле 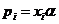определите набор вероятностей 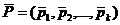, с которыми необходимо чередовать стратегии .

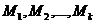Контрольные вопросы

1. Чем задача в условиях неопределенности отличается от задачи в условиях риска?

2. Что такое стратегия?

3. Что такое дуальная игра?

4. В каком случае игра может называться игрой с нулевой суммой?

5. В каком случае игра классифицируется как игра с противником?

6. Как составляется платежная матрица?

7. Чем элементы диагонали платежной матрицы отличаются от других элементов?

8. Что такое седловая точка?

9. В каком случае седловая точка может отсутствовать?

10. Что такое нижняя и верхняя цены игры?

Отчет о работе

Подготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите случайный параметр, взятый в рассмотрение, и обоснуйте его выбор. Приведите обоснование выбора его значений. Представьте платежную матрицу и результаты ее обработки. Определите факт наличие или отсутствия седловой точки. Если она существует, то приведите результаты решения задачи. Если седловой точки нет, то приведите набор стратегий, взятых в рассмотрение, представьте формулировку и результаты решения задачи определения набора вероятностей, с которыми будут чередоваться стратегии, и поставьте каждой в соответствие решение. Сформулируйте выводы, которые можно сделать по результатам выполненной работы.

Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б.

Игры с природой.

Отличительной особенностью игр с природой является то обстоятельство, что природа рассматривается как некоторая незаинтересованная инстанция, поведение которой неизвестно, но, во всяком случае, не содержит элемента враждебности и сознательного противодействия достижению наших целей. Как и в случае игр с противником, нам должна быть известна платежная матрица, соответствующая нашему выигрышу при различных своих стратегиях и состояниях (стратегиях) природы. Если в случае игры с противником предполагать определенные вероятности появления его стратегий не представлялось возможным, то в рассматриваемой ситуации нам полезно дополнительно располагать информацией о вероятностях появления возможных состояний природы, заданной, например, в виде смешанных стратегий

,

.

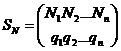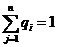Задача заключается в выборе в конкретных условиях наиболее выгодной собственной стратегии, а отбрасывать «невыгодные» с точки зрения природы стратегии нельзя. Исходя из этого в теории статистических решений [3] вводится понятие риска

,

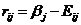где 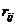наш риск при использовании стратегии 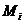в ответ на состояние природы 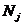, а 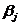- максимально возможный наш выигрыш при состоянии природы 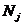. Если нам известны вероятности возможных состояний природы 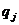, то было бы логичным в качестве своей стратегии принять одну из наших возможных стратегий 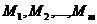, максимизирующую наш средний выигрыш

.

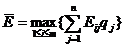Отметим, что указанная стратегия одновременно минимизирует средний риск.

Примечание. В случае игры с природой количество наших возможных стратегий 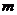может отличаться от количества возможных стратегий природы .

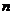При выборе оптимальной стратегии одну из существенных трудностей представляет определение конкретного набора вероятностей 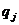. Если нет никаких гипотез о вероятности появления определенного состояния природы, то используется принцип недостаточного основания Лапласа, когда вероятности назначаются равными друг другу

.

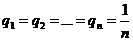Если у нас существуют некоторые предположения о вероятностях появления определенных событий, то мы можем их расставить в порядке убывания их правдоподобности (ранжировать) и поставить им в соответствие некоторый ряд чисел, определенный, в том числе, и экспертным путем. Отметим, что в любом случае справедливо утверждение

.