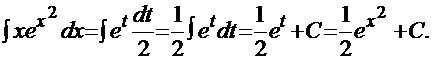Элементы аналитической геометрии.
Пример.Даны вершины треугольника ABC: A(-4;2), B(8;-6), C(2;6).
Найти: а) уравнение стороны AB;
б) уравнение высоты CH;
в) уравнение медианы AM;
г) уравнение прямой, проходящей через вершину C
параллельно стороне AB;
Решение: а) Используем уравнение прямой, проходящей через две точки A и B. Получим уравнение стороны AB: 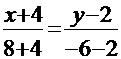 , откуда
, откуда 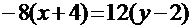 или
или 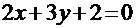 .
.
б) Высота опускается из точки C на сторону AB, угловой коэффициент которой 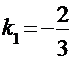 . Если обозначим угловой коэффициент стороны CH через
. Если обозначим угловой коэффициент стороны CH через 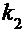 , то согласно условию перпендикулярности
, то согласно условию перпендикулярности 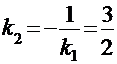 . Воспользуемся уравнением пучка прямых, проходящих через точку C:
. Воспользуемся уравнением пучка прямых, проходящих через точку C: 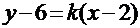 . Из этого пучка выберем прямую, перпендикулярную AB, придав значение
. Из этого пучка выберем прямую, перпендикулярную AB, придав значение 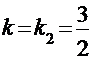 . Получим
. Получим 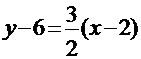 или
или 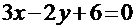 .
.
в) Предварительно найдем координаты середины М отрезка ВС: 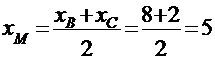 ,
, 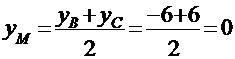 . По известным двум точкам составляем уравнение прямой АМ:
. По известным двум точкам составляем уравнение прямой АМ:
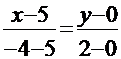 или
или 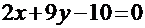 .
.
г) Воспользуемся уравнением пучка прямых, проходящих через точкуС: 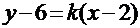 . Выберем из него прямую, параллельную прямой AB, придав значение
. Выберем из него прямую, параллельную прямой AB, придав значение 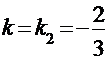 . Получим уравнение искомой прямой в виде
. Получим уравнение искомой прямой в виде
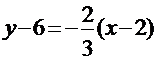 или
или 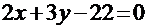 .
.
Предел и производная функции одной переменной.
Исследование функции одной переменной с помощью производной.
2.1Найти пределы функций, не пользуясь правилом Лопиталя.
а) 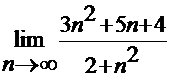 ,
,
Решение:
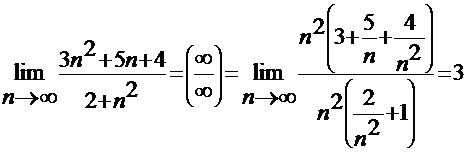 ,
,
б) 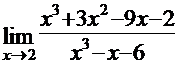 .
.
Решение: Устраняем неопределённость вида 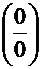 преобразованием:
преобразованием:
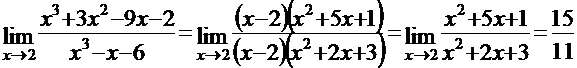 .
.
Производная функции
Производная функция 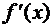 от функции
от функции 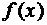 в данной точке
в данной точке 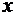 определяется равенством
определяется равенством
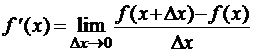 .
.
Таблица производных выглядит следующим образом:
1. 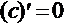 . 2.
. 2. 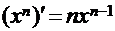 .
.
3. 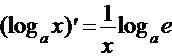 , в частности
, в частности 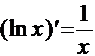 .
.
4. 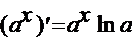 , в частности
, в частности 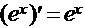 .
.
5. 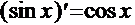 . 9.
. 9. 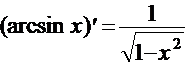 .
.
6. 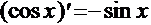 . 10.
. 10. 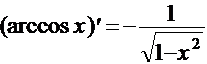 .
.
7. 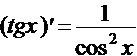 . 11.
. 11. 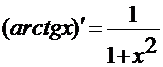 .
.
8. 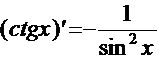 . 12.
. 12. 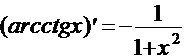 .
.
Основные правила дифференцирования
1. 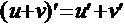 2.
2. 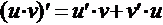 ,в частности,
,в частности,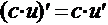 3.
3. 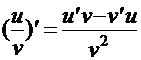 ,где
,где 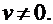
Задача. Найти производные следующих функций:
а) 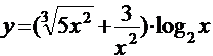 ; б)
; б) 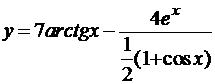 .
.
Решение.а) Преобразуем выражение в скобках, переходя к дробным и отрицательным показателям. Получим
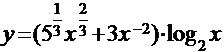 .
.
Используя правило дифференцирования произведения и суммы находим 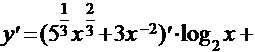
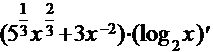 =
=
= 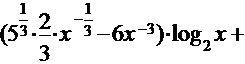
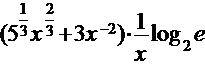 .
.
б) Проведем предварительное преобразование функции:
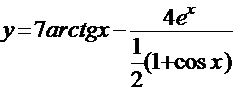 =
= 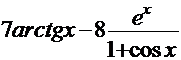 .
.
Используя правила дифференцирования произведения, суммы и частного, получим
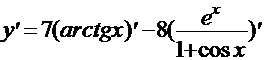 =
=
= 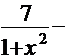
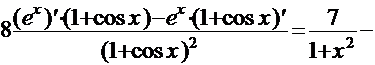
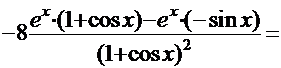
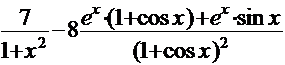 .
.
НЕОПРЕДЕЛЕННЫЙ И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Неопределенным интегралом 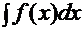 называется выражение
называется выражение 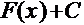 , где
, где 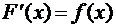 , а
, а 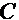 - произвольная константа, т.е.
- произвольная константа, т.е.
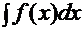 =
= 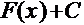 .
.
Замена переменных в неопределенном интеграле
Одним из основных методов интегрирования является метод замены переменных. Пусть требуется найти интеграл с непрерывной подынтегральной функцией
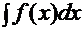 . (1)
. (1)
Сделаем замену переменных, положив
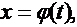 (2)
(2)
где функция 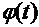 удовлетворяет следующим двум условиям:
удовлетворяет следующим двум условиям:
1) 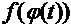 - непрерывная функция;
- непрерывная функция;
2) 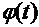 - непрерывно дифференцируемая функция, имеющая обратную функцию, тогда
- непрерывно дифференцируемая функция, имеющая обратную функцию, тогда 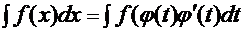 .
.
Задача 1. Найти неопределенный интеграл 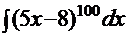 .
.
Решение: Положим, 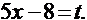 Дифференцируя это равенство, получим:
Дифференцируя это равенство, получим: 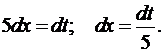
Но тогда 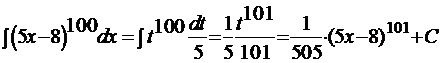 .
.
Задача 2. Найти неопределенный интеграл 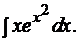
РHHешение: оложим 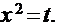 Такая замена очень естественна, так как, учитывая, что
Такая замена очень естественна, так как, учитывая, что 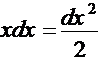 , наш интеграл можно записать в следующем порядке:
, наш интеграл можно записать в следующем порядке:
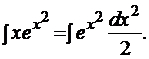 Итак,
Итак, 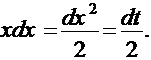
Тогда