Разложения функции в ряд Тейлора

замены переменных

логарифмирования

потенцирования

Решение:

Функция 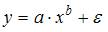является внутренне нелинейной, и для нее отсутствует прямое преобразование, которое превратит ее в линейную функцию. Только разложением функции в ряд Тейлора, то есть заменой данной функции суммой полиномов, можно привести данную функцию к линейному виду.

3. Для линеаризации нелинейной функции 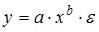может быть применен метод …

Логарифмирования и замены переменных

разложения функции в ряд Тейлора

потенцирования и замены переменных

обращения и замены переменных

Решение:

Функция 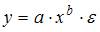является внутренне линейной и с помощью логарифмирования может быть преобразована к виду 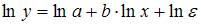, которая является линейной относительно логарифмов переменных. Сделав замену переменных , , 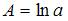, , 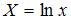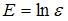получим линейную функцию 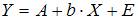. Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.

Тема 16: Оценка качества нелинейных уравнений регрессии

1. При расчете уравнения нелинейной регрессии 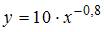, где y – спрос на продукцию, ед.; x – цена продукции, руб., выяснилось, что доля остаточной дисперсии в общей меньше 20%. Коэффициент детерминации для данной модели попадает в отрезок минимальной длины …

[0,8; 1]

[0,2; 1]

[0; 0,2]

[0; 0,8]

Решение:

Доля остаточной дисперсии в общей меньше 20%, значит, доля объясненной регрессии в общей больше 80%, другими словами, коэффициент детерминации больше 0,8. Поскольку коэффициент детерминации может принимать значения только в интервале [0, 1], то отрезком минимальной длины, в который попадает коэффициент детерминации для данной модели, будет отрезок [0,8; 1].

2. По 20 регионам страны изучалась зависимость уровня безработицы y (%) от индекса потребительских цен x (% к предыдущему году) и построено уравнение в логарифмах исходных показателей: 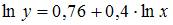. Коэффициент корреляции между логарифмами исходных показателей составил 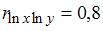. Коэффициент детерминации для модели в исходных показателях равен …

0,64

0,8

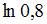
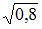
Решение:

Коэффициент детерминации для модели в исходных показателях в данном случае будет равен коэффициенту детерминации для модели в логарифмах исходных показателей, который вычисляется как квадрат коэффициента корреляции, то есть 0,64.

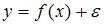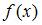3. Для регрессионной модели , где – нелинейная функция, 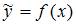– рассчитанное по модели значение переменной 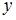, получены значения дисперсий: 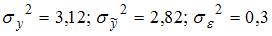. Не объяснена моделью часть дисперсии переменной 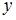, равная …

0,096

0,904

0,106

10,4

Решение:

Значение индекса детерминации R² характеризует долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии). Разность (1-R²) характеризует долю дисперсии зависимой переменной, необъясненную уравнением, эту величину и необходимо определить в задании. Воспользуемся формулой для расчета R²: 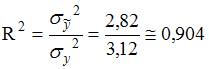. Следовательно, разность 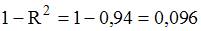. Таким образом, часть дисперсии переменной 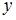, необъясненная моделью, равна 0,096. Можно также рассчитать это значение через отношение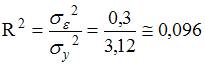

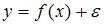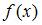4. Для регрессионной модели , где – нелинейная функция, 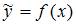– рассчитанное по модели значение переменной 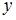, получено значение индекса корреляции R = 0,64. Моделью объяснена часть дисперсии переменной 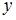, равная …

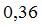
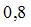
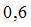
Решение:

Величина, характеризующая долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии), называется индексом (коэффициентом) детерминации – R². Значения индекса детерминации R² и индекса корреляции R для нелинейных регрессионных моделей связаны соотношением 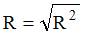. Следовательно, значение .

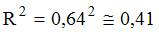5. По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии 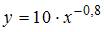, где y – спрос на продукцию, ед.; x – цена продукции, руб. Если фактическое значение t-критерия Стьюдента составляет –2,05, а критические значения для данного количества степеней свободы равны 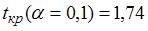, , 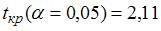, 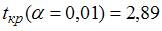то …

при уровне значимости 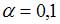можно считать, что эластичность спроса по цене составляет –0,8

при уровне значимости 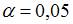можно считать, что эластичность спроса по цене составляет –0,8

эластичность спроса по цене составляет –0,8

при уровне значимости 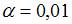можно считать, что эластичность спроса по цене составляет –0,8

Решение:

Для проверки значимости коэффициентов нелинейной регрессии, после линеаризации, как и для уравнения парной линейной регрессии, применяется стандартный алгоритм критерия Стьюдента. Для b формулируется нулевая гипотеза 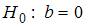при альтернативной гипотезе 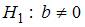. Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента 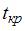для требуемого числа степеней свободы и уровня значимости. Если 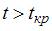, коэффициент 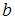значим; если 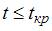, коэффициент 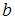незначим. В нашем случае при уровне значимости 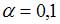коэффициент 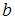значим, а при уровнях значимост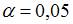и и 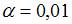незначим.

Тема 17: Временные ряды данных: характеристики и общие понятия

1. В состав любого временного ряда, построенного по реальным данным, обязательно входит _____ компонента.

Случайная

сезонная

трендовая

циклическая

Решение:

Ряд, построенный по реальным данным, может не содержать тренда, сезонной (циклической) компоненты, однако, он обязательно содержит случайную компоненту.

2. Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике …

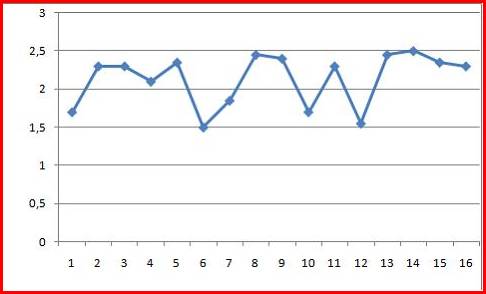
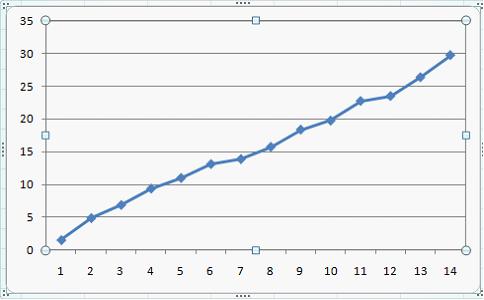
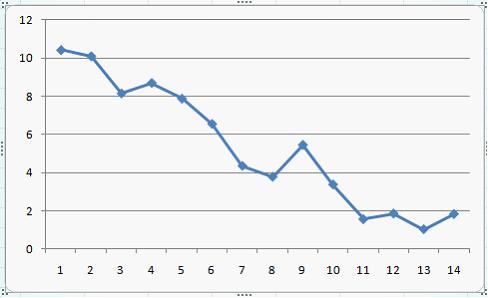
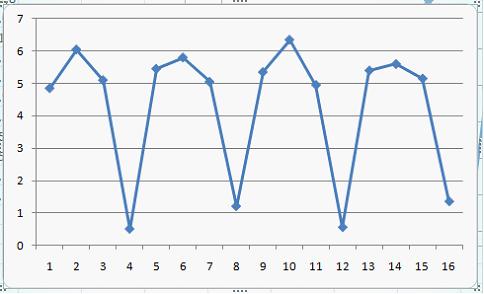
Решение:

График ряда, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, будет колебаться относительно своего среднего значения.

3. Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …

Временным рядом

тенденцией

коррелограммой

автокорреляционной функцией

Решение:

Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется временным рядом.

4. Выраженную положительную тенденцию содержит ряд …

-

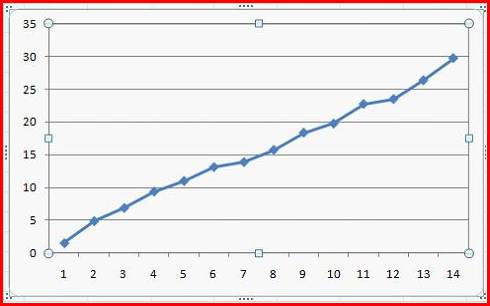
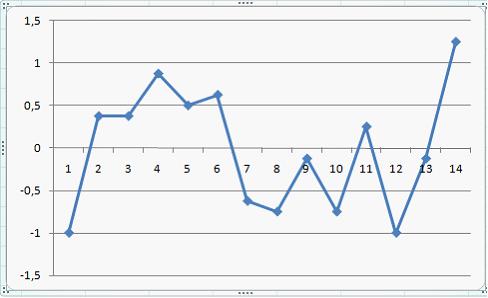Решение:

Ряд имеет выраженную положительную тенденцию, если уровни ряда увеличиваются с увеличением периода времени t.

Тема 18: Структура временного ряда

1. Значение коэффициента автокорреляции первого порядка характеризует …

Тесноту линейной связи

качество модели временного ряда

тесноту нелинейной связи

значимость тренда

Решение:

Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков коэффициента автокорреляции. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка, а само значение коэффициента корреляции рассчитывается по аналогии с парным коэффициентом линейной корреляции и характеризует тесноту линейной связи между двумя переменными. Поэтому варианты «качество модели временного ряда», «тесноту нелинейной связи» и «значимость тренда» являются неверными.

2. Дана автокорреляционная функция ++ временного ряда ++

Верным будет утверждение, что ряд …