Статистика Дарбина – Уотсона
тест Уайта
критерий Гольдфельда – Квандта
тест Парка
Решение:
Для обнаружения автокорреляции остатков используется расчет статистик Дарбина – Уотсона. Тест Уайта, критерий Гольдфельда – Квандта, тест Парка применяются для обнаружения гетероскедастичности остатков.
2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений 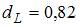 ,
, 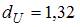 . По данным характеристикам можно сделать вывод о том, что …
. По данным характеристикам можно сделать вывод о том, что …
Автокорреляция остатков отсутствует
статистика Дарбина – Уотсона попадает в зону неопределенности
есть положительная автокорреляция остатков
есть отрицательная автокорреляция остатков
Решение:
Дано, что коэффициент автокорреляции остатков первого порядка равен –0,3, 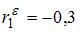 . Рассчитаем статистику Дарбина – Уотсона по формуле
. Рассчитаем статистику Дарбина – Уотсона по формуле 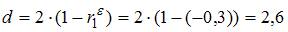 . Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений
. Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений 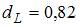 ,
, 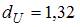 , которые разбивают отрезок от 0 до 4 на пять частей.
, которые разбивают отрезок от 0 до 4 на пять частей.
В интервале [0; 0,82] есть положительная автокорреляция остатков;
в интервале (0,82; 1,32] – зона неопределенности;
в интервале (1,32; 2,68] нет автокорреляции остатков;
в интервале (2,68; 3,12] – зона неопределенности;
в интервале (3,12; 4] есть отрицательная автокорреляция остатков.
В нашем случае значение статистики Дарбина–Уотсона d=2,6 попадает в интервал (1,32; 2,68]. Значит, можно сделать вывод, что нет автокорреляции остатков.
3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле 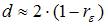 , где
, где 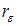 – значение коэффициента автокорреляции остатков модели. Минимальная величина значения
– значение коэффициента автокорреляции остатков модели. Минимальная величина значения 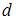 будет наблюдаться при ________ автокорреляции остатков.
будет наблюдаться при ________ автокорреляции остатков.
Положительной
отрицательной
нулевой
бесконечно малой
Решение:
Значение коэффициента автокорреляции остатков модели 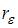 рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если
рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если 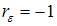 , то
, то 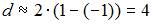 ; если
; если 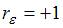 , то
, то 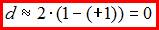 . Поэтому значение
. Поэтому значение 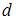 меняется от 0 до 4. Минимальное значение
меняется от 0 до 4. Минимальное значение 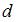 равно 0 для случая, когда
равно 0 для случая, когда 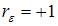 , то есть для положительной автокорреляции остатков.
, то есть для положительной автокорреляции остатков.
4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.
Гетероскедатичность
случайный характер
нулевая средняя величина
отсутствие автокорреляции
Решение:
Условия, необходимые для несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК.
Исследования остатков предполагают проверку наличия следующих пяти предпосылок МНК:
– случайный характер остатков;
– нулевая средняя величина остатков, не зависящая от 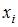 ;
;
– гомоскедастичность остатков;
– отсутствие автокорреляции остатков;
– подчинение остатков нормальному закону распределения.
Гетероскедатичность остатков не является предпосылкой МНК.
5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле 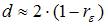 , где
, где 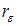 – значение коэффициента автокорреляции остатков модели. Максимальная величина значения
– значение коэффициента автокорреляции остатков модели. Максимальная величина значения 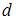 будет наблюдаться при ________ автокорреляции остатков.
будет наблюдаться при ________ автокорреляции остатков.
Отрицательной
положительной
нулевой
бесконечно малой
Решение:
Значение коэффициента автокорреляции остатков модели 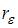 рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если
рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если 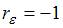 , то
, то 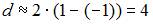 ; если
; если 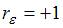 , то
, то 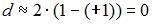 . Поэтому значение
. Поэтому значение 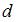 меняется от 0 до 4. Максимальное значение
меняется от 0 до 4. Максимальное значение 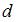 равно 4 для случая, когда
равно 4 для случая, когда 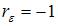 , то есть для отрицательной автокорреляции остатков.
, то есть для отрицательной автокорреляции остатков.
Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
1. Пусть 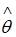 – оценка параметра
– оценка параметра 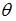 регрессионной модели, полученная с помощью метода наименьших квадратов;
регрессионной модели, полученная с помощью метода наименьших квадратов; 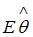 – математическое ожидание оценки
– математическое ожидание оценки 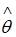 . В том случае если
. В том случае если 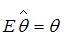 , то оценка обладает свойством …
, то оценка обладает свойством …
Несмещенности
состоятельности
эффективности
смещенности
Решение:
Желательными свойствами оценок параметров регрессионной модели являются состоятельность, несмещенность и эффективность. Понятие несмещенности оценки формулируется следующим образом: «Оценка 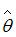 параметра
параметра 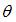 называется несмещенной, если математическое ожидание
называется несмещенной, если математическое ожидание 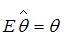 »; где
»; где 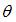 – истинное значение параметра, вычисленное для генеральной совокупности. Поэтому правильный ответ – «несмещенности».
– истинное значение параметра, вычисленное для генеральной совокупности. Поэтому правильный ответ – «несмещенности».
2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …
-1
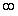
Решение:
Желательными свойствами оценок параметров регрессионной модели являются состоятельность, несмещенность и эффективность. Понятие несмещенности оценки формулируется следующим образом: «Оценка 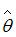 параметра
параметра 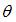 называется несмещенной, если математическое ожидание
называется несмещенной, если математическое ожидание 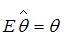 »; где
»; где 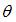 – истинное значение параметра, вычисленное для генеральной совокупности. Математическое ожидание
– истинное значение параметра, вычисленное для генеральной совокупности. Математическое ожидание 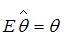 в том случае, если
в том случае, если 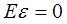 .
.
3. Несмещенность оценок параметров регрессии означает, что …
