Расчёт характеристик сложного трубопровода с разветвлённым участком и двумя гидромоторами

Как уже отмечалось, эквивалентная схема гидропривода подъёмного механизма представляет собой сложный трубопровод, состоящий из 4-х простых трубопроводов, причём 2-й и 3-й включены параллельно между 1-м и 4-м трубопроводами.

На основании эквивалентной схемы на рисунке 2.5 уравнения характеристик простых трубопроводов можно представить в виде:

– для 1-го участка 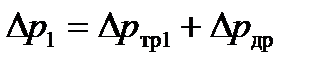и с учётом (2.23) и (2.26)

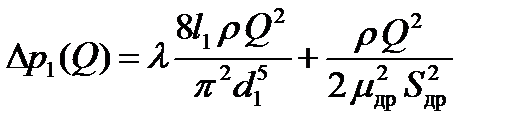; (2.35)

для построения этой характеристики при ручном счёте удобно это уравнение представить в виде

,

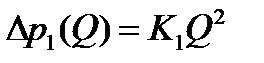где

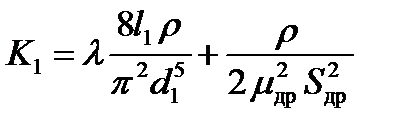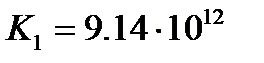. кг/м⁷;

- для 2-го участка 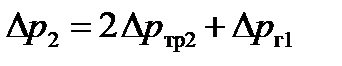определяем по формуле (2.7), а потери в гидромоторе по формуле (2.31)

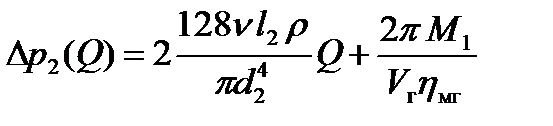, (2.36)

при ручном счёте это уравнение представляется в виде

,

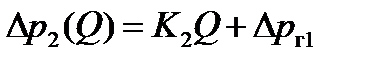где

,

,

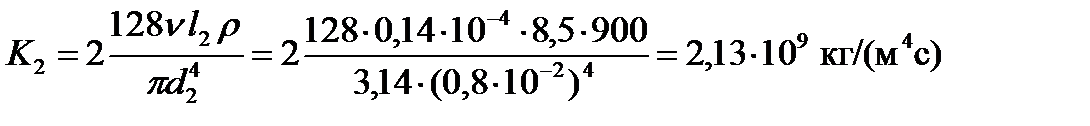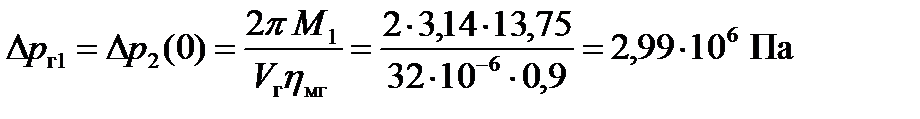- для 3-го участка 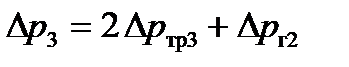с ламинарным течением – аналогично (2.36)

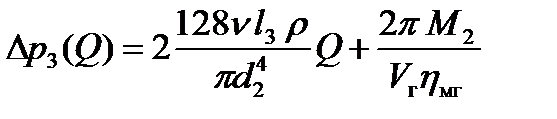, (2.37)

при ручном счёте это уравнение представляется в виде

,

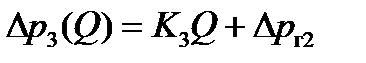где с учётом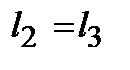

,

,

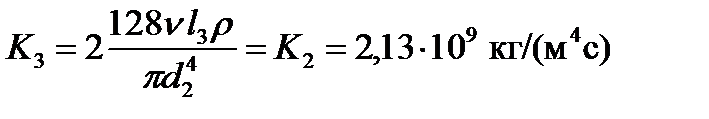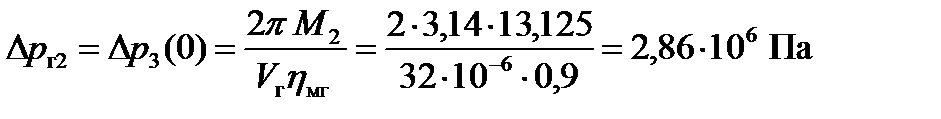- для 4-го участка 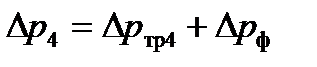с учётом (2.24) и (2.26)

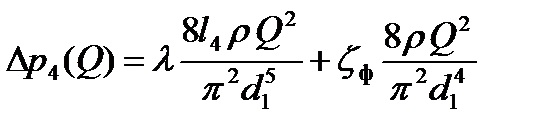, (2.38)

или

,

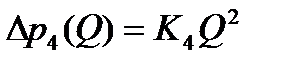где

.

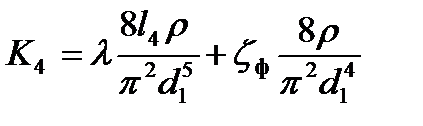Заметим, что участки 1 и 4 включены последовательно, поэтому для них можно написать общее уравнение 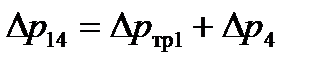, построить характеристику и не проводить в дальнейшем их графического сложения.

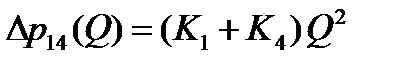, (2.39)

в этом выражении

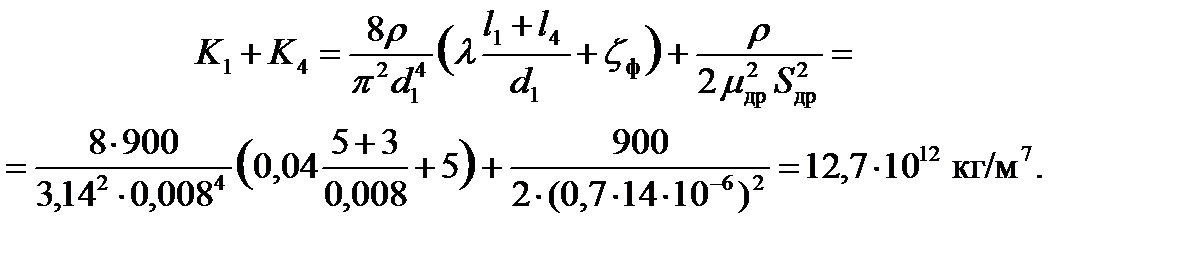
Поскольку характеристики 2-го и 3-го участков линейны, для их построения достаточно двух точек, например, при 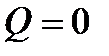и .

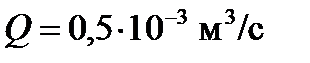Для построения нелинейной характеристики 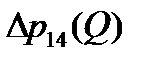рекомендуется определить 5–6 точек, задаваясь произвольными значениями 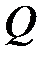, в интервале 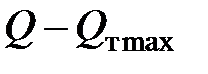. Окончательные результаты расчетов заносим в таблицу 2.2.

Таблица 2.2 – Результаты расчёта потерь давления в функции от расхода

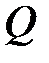, м3/с		0,2.10– 3	0,3.10– 3	0,4.10– 3	0,5.10– 3	0,6.10– 3
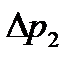, МПа	2,99				4,27
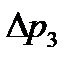, МПа	2,86				4,12
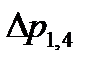, МПа		0,51	1,14	2,03	3,18	4,57

По данным таблицы 2.2 на графике (рис. 2.11) строим характеристик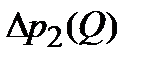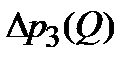и , и 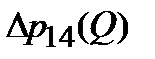. Характеристики участков 2 и 3, описываемые уравнениями (2.36) и (2.37), имеют вид прямых линий, суммарная характеристика 1-го и 4-го участков 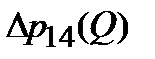, описываемая уравнением (20), имеет криволинейные вид как показано на рисунке 2.11.

Затем по правилам графического сложения характеристик параллельных участков 2 и 3 (складываются абсциссы точек потерь давления ∆р = f(Q) обоих участков, взятых при одной и той же ординате, иными словами, складываются кривые потерь давления обоих участков по горизонтали) получаем суммарную характеристику участков 2 и 3 (ломаная линия LMN – 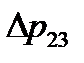на рисунке 2.12). Заметим, что при сложении прямых, достаточно провести сложение по двум точкам.

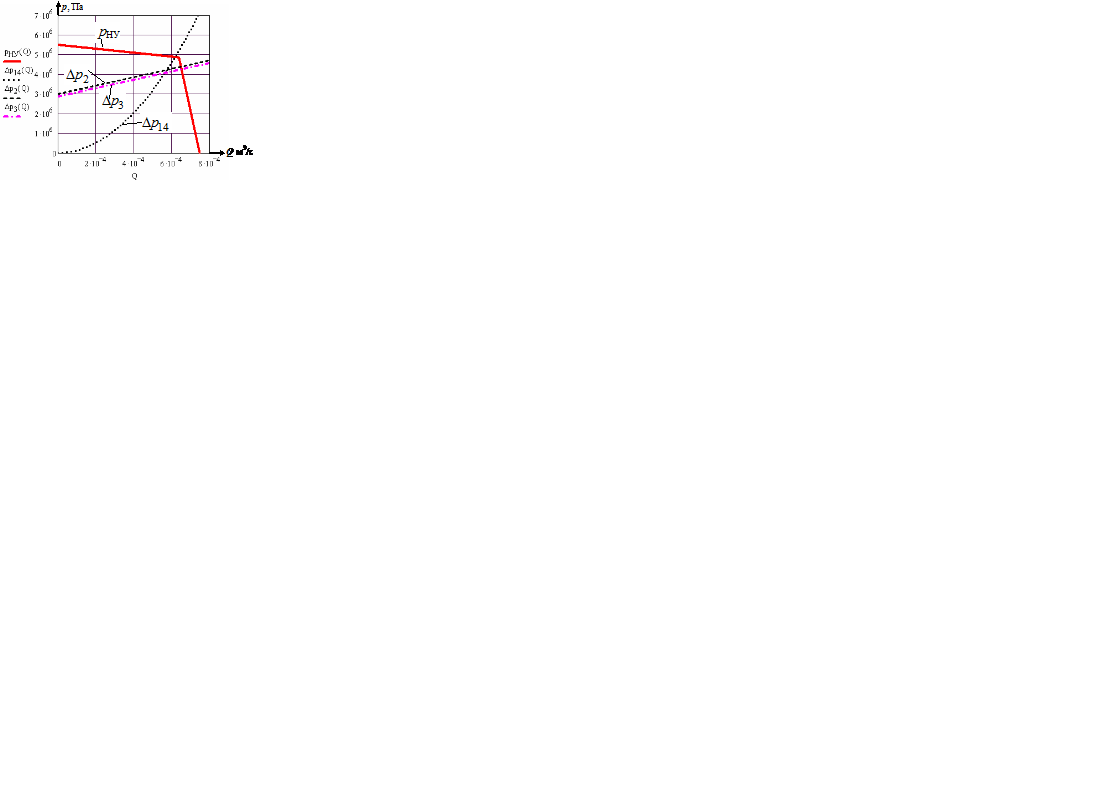
Рисунок 2.11 – Характеристики 2-го и 3-го участков и совместная характеристика 1-го и 4-го участков

Данную зависимость можно получить аналитически. Участок LM ломаной линии совпадает с отрезком характеристики 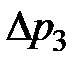. Давление в точке 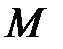соответствует давлению на характеристике 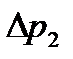при нулевом расходе

.

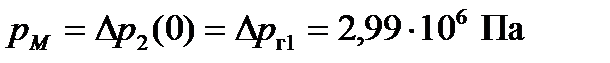Объёмный расход в точке 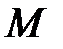определится их уравнения характеристики 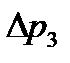(2.18) при давлении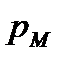

.

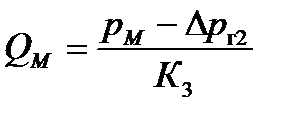
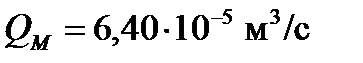Для построения участка 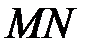выбираем на ней произвольную точку 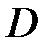с давлением 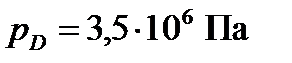. Для этого давления находим объёмные расходы:

- для характеристик второго участка

, ,

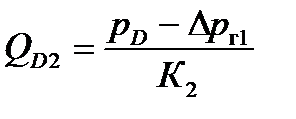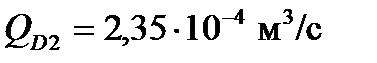- для характеристик третьего участка

, ,

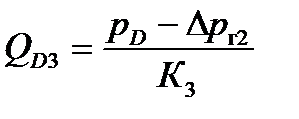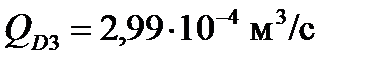- для суммарной характеристики второго и третьего участков

, .

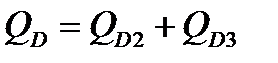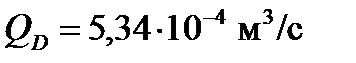Из подобия треугольников находится уравнение линии 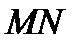суммарной характеристики второго и третьего участков

.

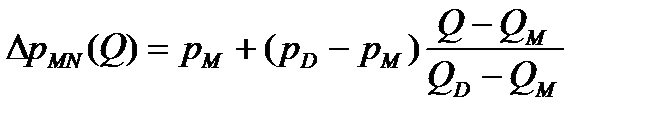Суммарная характеристика второго и третьего участков – ломаная линия 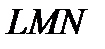– определяется Mathcad из условия

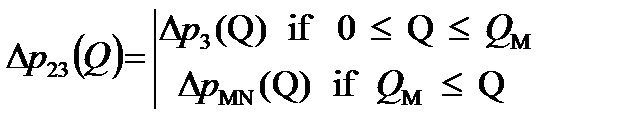. (2.40)

Далее проводим графическое сложение полученной характеристики 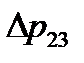(ломаная линия 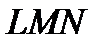) с характеристикой 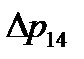(2.39) по оси давлений 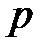и в результате получаем суммарную характеристику всего сложного трубопровода – линия 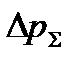на рисунке 2.12:

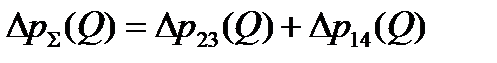. (2.41)

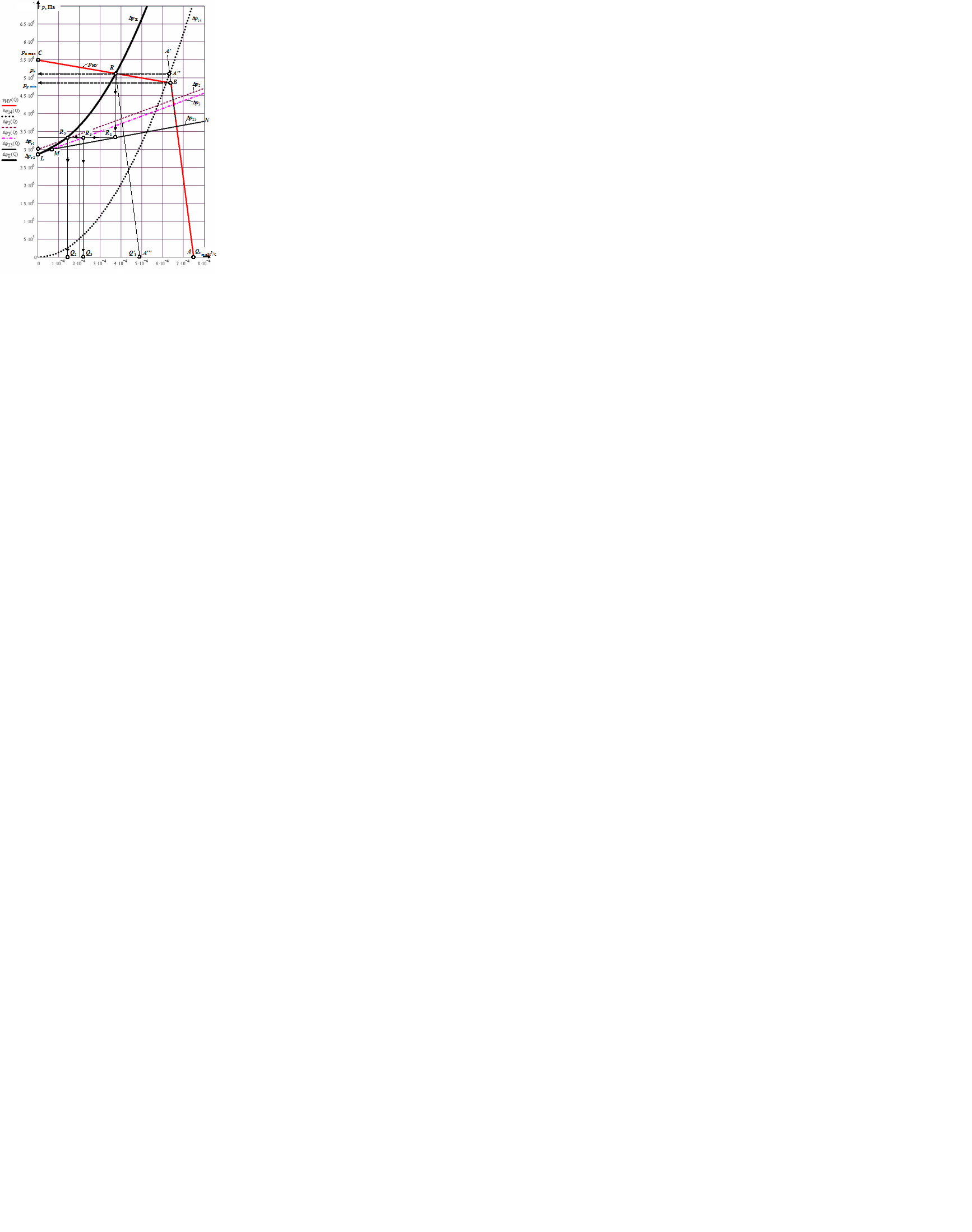
Рисунок 2.12 – Графики, полученные по результатам расчета