Установившаяся фильтрация несжимаемой жидкости по закону Дарси

Установившийся фильтрационный поток жидкости или газа называется одномерным в том случае, когда давление и скорость фильтрации являются функциями только одной координаты, взятой по линии тока.

К простейшим одномерным фильтрационным потокам относятся:

1) прямолинейно - параллельный;

2) плоскорадиальный;

3) радиально - сферический.

5.2.1. Прямолинейно-параллельная фильтрация м жидкости (приток к галерее)

Прямолинейно-параллельная фильтрация имеет место в том случае, когда векторы скоростей фильтрации параллельны между собой.

Если пласт горизонтальный, кровля и подошва непроницаемы, толщина пласта h и ширина пласта В всюду одинаковы, то в плане пласт представится прямоугольником (рис. 5.1). Если в первом сечении пласта, соответствующем границе пласта с областью питания, поддерживается давление р_к. а в другом сечении, совпадающем, например, с дренажной галереей и отстоящем от первого сечения на расстоянии l, поддерживается давление р_г. то будет установившееся прямолинейно-параллельное движение.

Направим ось ОХ вдоль линии тока.

Считая, что фильтрация происходит по закону Дарси, пласт однородный по пористости и проницаемости, можем определить объемный дебит

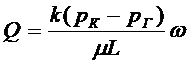(5,13)

где ω=Bh - площадь сечения пласта, нормального к направлению движения.

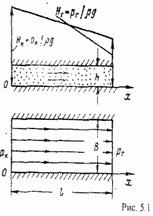
Давление в любом сечении пласта

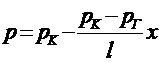(5,14)

и время, втечение которого частицы пройдут путь x,

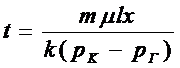(5.15)

5.2.2. Плоскорадиальное напорное движение несжимаемой

Жидкости. Приток к совершенной скважине.

Формула Дюпюи

При плоскорадиальном движении векторы скорости фильтрации направлены по радиусам к оси скважины, поэтому давление и скорость фильтрации зависят только от одной координаты r. При этом во всех горизонтальных плоскостях поле скоростей и давлений будет одинаковым.

Примером плоскорадиального фильтрационного потока является приток к гидродинамически совершенной скважине, вскрывшей горизонтальный пласт бесконечной протяженности на всю толщину h и сообщающейся с пластом через полностью открытую боковую поверхность цилиндра, отделяющую ствол скважины от продуктивного пласта.

Поток будет также плоскорадиальным при притоке к совершенной скважине радиуса г_с (или оттоке от скважины), расположенной в центре ограниченного горизонтального цилиндрического пласта толщиной h и радиусом R_K (рис.5. 2).

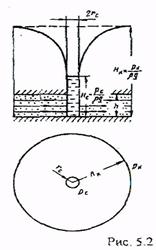
Если на внешней границе пласта, совпадающей с контуром питания, поддерживается постоянное давление р_к, а на забое скважины постоянное давление р_с, пласт однороден по пористости и проницаемости, фильтрация происходит по закону Дарси, то объемный дебит скважины определится по формуле Дюпюи:

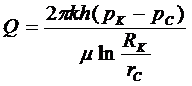(5.16)

где μ - динамический коэффициент вязкости.

Закон распределения давления определяется по одной из формул:

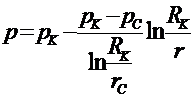(5.17)

либо

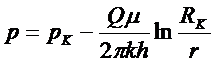(5.18)

либо

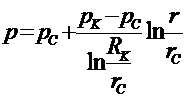(5.19)

Линия р = р(r) называется депрессионной кривой давления. Характерно, что при приближении к скважине градиенты давления и скорости фильтрации рис.5.2 резко возрастают. При построении карты изобар следует учитывать, что радиусы изобар изменяются в геометрической прогрессии, в то время как давление на изобарах изменяется в арифметической прогрессии.

Индикаторная линия - зависимость дебита скважины от депрессии Δp=p_K –p_C при притоке к скважине в условиях справедливости закона Дарси представляет собой прямую линию, определяемую уравнением Q=KΔp.

Коэффициент продуктивности

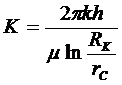(5.20)

численно равен дебиту при депрессии, равной единице.

Закон движения частиц вдоль линии тока, если при t=0 частица находилась в точке с координатой r=r₀, описывается уравнением

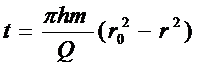(5.21)

или

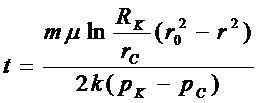(5.21,а)

Средневзвешенное по объему порового пространства Q пластовое давление

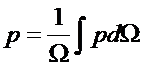(5.22)

где

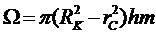
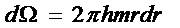
Подставляя выражение для р (5.17), выполняя интегрирование и пренебрегая всеми членами, содержащими r_c²:, получим

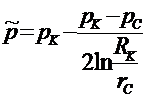(5.23)

Закон распределения давления и формула дебита при нарушении закона Дарси при притоке к совершенной скважине получаются из двучленной формулы

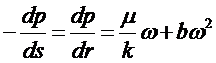(5.24)

Подставляя выражение для скорости фильтрации

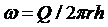
в (5.24) и разделяя переменные, получим

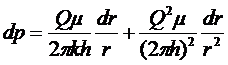(5.25)

Интегрируя по р в пределах от р_с. до р_к и по r в пределах от rc,. до Rkбудем иметь

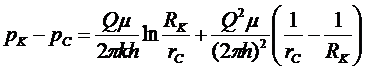(5.26)

Решая полученное квадратное уравнение, находим дебит скважины Q. Интегрируя (5.25) по р в пределах от р_с. до р_к и по r в пределах от r_с до R_K, найдем закон распределения давления

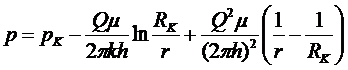(5.27)

Как видно из (5.26), индикаторная линия при нарушении закона Дарси

является параболой.

Если фильтрация происходит по закону Краснопольского, то дебит определяется по формуле

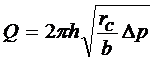(5.28)