Нелиейные операции над векторами. Метод координат

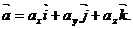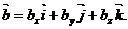Скалярным произведением двух векторов и называется число, определяемое равенством

.

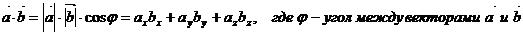Свойства скалярного произведения векторов:

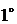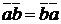. (переместительное свойство)

.

.

.

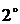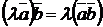
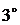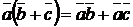
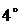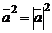
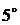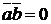. , если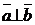

Векторным произведением 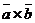двух векторов 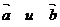называется вектор, длина которого равна

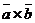
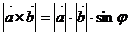,где 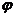- угол между

векторами .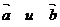

И который направлен перпендикулярно

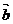векторам 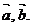Векторы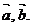 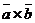образуют

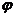так называемую правую тройку.

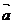
Рис. 1

Вектор 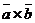находится по формуле:

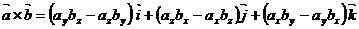(5)

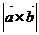Геометрически равна площади параллелограмма, построенного на векторах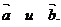

Смешанное произведение 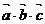векторов 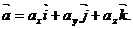, , 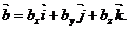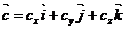есть число, определяемое формулой:

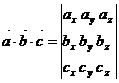
Модуль 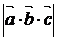смешанного произведения равен объёму параллелепипеда, построенного на векторах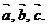

Метод координат.

Аналитическая геометрия изучает геометрические образы алгебраическими методами. Аппаратом аналитической геометрии является метод координат, разработанный Декартом в XVII веке. В основе метода координат лежит понятие системы координат.

Две взаимно перпендикулярные оси О_х и О_у, имеющие общее начало О и одинаковую масштабную единицу, образуют прямоугольную систему координат. Ось О_х называется осью абсцисс, ось О_у – осью ординат.

В прямоугольной системе координат О_ху точку М, имеющую координаты х и у, обозначают М(х; у), где х – абсцисса точки, а у – её ордината.

Пусть в прямоугольной системе координат заданы точки М₁(х_1, у₁) и М₂(х₂;у₂). Расстояние между ними определяется по формуле:

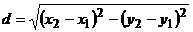(1)

Три точки плоскости, не лежащие на одной прямой образуют треугольник.

Теорема.Для любых трех точек А(х₁;у₁),В(х₂;у₂) и С(х₃;у₃), не лежащих на одной прямой, площадь S треугольника АВС вычисляется по формуле

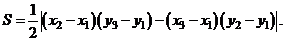(2)

Пусть на плоскости дан произвольный отрезок М₁М₂ и пусть М – любая точка этого отрезка, отличная от точки М₂ .

Координаты точки М(х;у) делящей отрезок между точками М₁(х₁;у₁) и М₂(х₂;у₂) в заданном отношении λ, определяются по формулам:

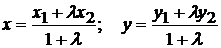(3)

При λ=1 получаем формулы для координат середины отрезка:

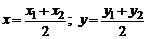(4)

Прямая на плоскости.

Важнейшим понятием аналитической геометрии является уравнение линии.

Определение. Уравнение F(x, y)=0 называется уравнением линии L (в заданной системе координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

Любая прямая на плоскости задается уравнением первой степени относительно переменных х и у.

Прямую можно задать одним из следующих уравнений:

1. Уравнение прямой с угловым коэффициентом k (k – тангенс угла наклона прямой к положительному направлению оси Ox)

у=kх+b (1)

2. Уравнение прямой с заданным угловым коэффициентом, проходящей через данную точку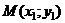

)

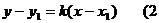3. Уравнение прямой, проходящей через две данные точки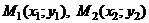

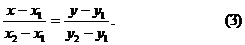
4. Уравнение прямой в «отрезках»

здесь a и b –отрезки, которые отсекает прямая на осях О_х и О_у соответственно.

5. Нормальное уравнение прямой

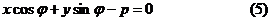
здесь р – длина перпендикулярна, опущенного из начала координат на прямую, a 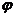-угол образованный этим перпендикуляром с положительным направлением оси Ох.

6. Уравнение прямой проходящей через точку 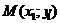, в данном направлении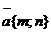

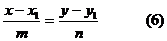
7. Общее уравнение прямой

Ax=By+С=0. (7)

Здесь A, B и C постоянные коэффициенты, причем 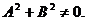Если какой-то коэффициент равен 0, то получаем неполные уравнения прямой.

А) Если А=0, тогда By+C=0 это уравнение определяет прямую, параллельную оси О_х.

б) Если В=0, то уравнение Ax+C=0 определяет прямую, параллельную оси О_у.

в) Если С=0, то уравнение Ax+By=0 задает прямую, проходящую через начало координат.

Г) Если А=С=0, то уравнение By=0 определяет прямую совпадающую с осью Ох.

Д) При В=С=0 прямая Ах=0 совпадает с осью Оу.

Прямые на плоскости могут пересекаться, быть параллельными или перпендикулярными.

Если прямые заданы уравнениями с угловым коэффициентом

y=k₁x+b₁ и y=k₂x+b₂ , (8)

то острый угол между прямыми определяется по формулам

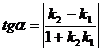. (9)

Если же прямые заданы общими уравнениями

А₁х+В₁у+С₁=0 и А₂х+В₂у+С₂=0, (10)

то угол между ними можно найти по формулам

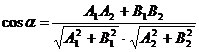(11)

Пусть прямые заданы уравнениями (8). Прямые параллельны, если tg a=0, тогда

k₂=k₁ (12)

условие параллельности двух прямых. Условие перпендикулярности определяет равенство

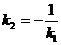(13)

Если прямые заданы уравнениями (10), то условия параллельности и перпендикулярности примут вид:

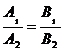, (14)

А₁А₂+В₁В₂=0. (15)

Уравнение плоскости.

Пусть заданы прямоугольная система координат Oxyz, произвольная плоскость П, точка 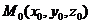и вектор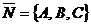

Уравнение

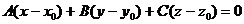(1)

определяет плоскость, проходящую через точку 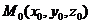перпендикулярно вектору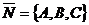

В уравнении (1) раскроем скобки

.

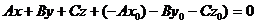Выражение, стоящее в скобках обозначаем через Д, тогда получим

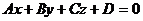(2)

Уравнение (2) называется общим уравнением плоскости. Вектор 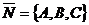называется нормальным вектором плоскости.

Если в общем, уравнении плоскости коэффициент 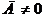то, разделив все члены уравнения на – Д, уравнение плоскости можно привести к виду

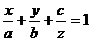(3)

здесь 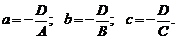Это уравнением плоскости в «отрезках» в нем а, b и с соответствует абсциссе, ординате и аппликате точек пересечения плоскости с осями координат О_х, О_у, О_z.

При любом расположении (2) плоскостей П₁, П₂

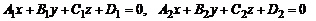(4)

в пространстве один из углов 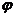между ними равен углу между их нормальными векторами и 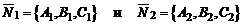вычисляется по формуле

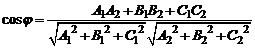(5)

Если два уравнения (4) определяют одну и ту же плоскость, то их коэффициенты пропорциональны

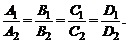(6)

Если плоскости П₁ и П₂ параллельны, то коллениарны их нормальные векторы 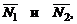и наоборот. Но тогда

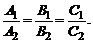(7)

Условие (7) является условием параллельности плоскостей.

Если же плоскости П₁ и П₂ перпендикулярны, то перпендикулярны их нормальные векторы 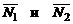. Но тогда их скалярное произведение равно 0, т.е.

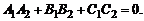(8)

Равенство (8) определяет условие перпендикулярности плоскостей.