Интервальные оценки параметров

Выборка, полученная из генеральной совокупности, содержит n значений признака - случайной величины Х. Найденные значения точечных характеристик в свою очередь будут случайными величинами, меняющимися от выборки к выборке. Однако они используются для оценки неслучайных числовых параметров генеральной совокупности – математического ожидания (генеральной средней) и дисперсии (генеральной дисперсии). С этим обстоятельством связана необходимость ввести в рассмотрение понятия интервальных оценок параметров – оценок, определяемых двумя числами, границами некоторого интервала.

Интервальной оценкой какого-либо оцениваемого параметра служит доверительный интервал.

Доверительный интервал – интервал со случайными границами, вычисляемыми по выборке, который с заданной исследователем (доверительной) вероятностью «накрывает» оцениваемый параметр. Как правило, выбирается симметричный интервал относительно .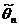

Пусть исследуемый признак распределен в соответствии с нормальным законом распределения.

Интервальная оценка для генеральной средней:

а) при известной среднеквадратической ошибке измерения:

,

где - генеральная средняя (математическое ожидание); - известное среднее квадратическое отклонение; n - объем выборки; t определяется из условия , где - функция Лапласа, заданная таблично; - доверительная вероятность, назначаемая исследователем.

б) при неизвестной среднеквадратической ошибке

,

где s - среднее выборочное квадратическое отклонение; - табулированная функция, построенная на основе распределения Стьюдента.

Интервальная оценка для генеральной дисперсии

,

где D – генеральная дисперсия k =n-1 или k=n-m; - квантили - распределения, зависящие от kдоверительной вероятности .

Интервальная оценка для генерального среднего квадратического отклонения:

,

где - генеральное среднее квадратическое отклонение, - таблично заданная функция.

Проверка статистических гипотез

В основе понятия статистической гипотезы лежит принцип практической уверенности: если вероятность события А очень мала, то при однократном проведении испытания можно быть уверенным в том, что событие А не произойдет, и в практической деятельности вести себя так, будто событие А вообще невозможно.

Вопрос о конкретной величине вероятности события А решает исследователь.

Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения.

Проверяемую гипотезу называют нулевой и обозначают . Наряду с нулевой рассматривают альтернативную, конкурирующую гипотезу , являющуюся логическим отрицанием . Правило, по которому гипотеза принимается или отвергается, называется статистическим критерием.