Плоскость и прямая в пространстве.

3.1. Уравнение поверхности в пространстве.

Положение точки в пространстве определяется тремя координатами.

Прямоугольная декартова система координат в пространстве представляет собой три перпендикулярные прямыеOx, Oy, Oz, снабженные масштабами и направлениями. Такие прямые называются координатными осями. Координатами точкиM₀(x₀,y₀,z₀) называются координаты оснований перпендикуляров, опущенных из этой точки на координатные оси.

Уравнением поверхности (в выбранной системе координат) называется такое уравнение с тремя переменными F(x,y,z)=0, которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и только они.

3.2. Плоскость в пространстве.

Пусть плоскость проходит через точку M₀(x₀,y₀,z₀) перпендикулярно вектору 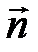=(А,B,C). Этими условиями определяется единственная плоскость в пространствеOxyz. Вектор 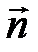называется нормальным вектором плоскости. Для произвольной точки плоскости M(x,y,z) («текущей точки») векторы 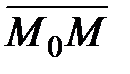= (x-x₀, y-y₀, z-z₀) и 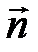должны быть перпендикулярны. Следовательно,

скалярное произведение этих векторов равно нулю, т.е. ( 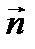, 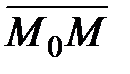)=0. Полученное уравнение представим в координатной форме:

А(x-x₀) + В(y-y₀) + C(z-z₀) = 0. (18)

M

M0

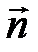Уравнение (18) представляет уравнение плоскости, перпендикулярной данному вектору = (А,B,C) и проходящей через данную точку M₀(x₀,y₀,z₀) (рис. 9).

y

x

Рис. 9

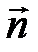Пример 16. Составить уравнение плоскости, проходящей через точку M₀(-1,0,2) и перпендикулярной вектору = (2,5,-1).

Решение. Искомое уравнение имеет вид 2(x+1)+5(y-0)-1(z-2)=0. ■

Уравнение плоскости, записанное в виде

Аx + By + Cz + D = 0 (19)

(где D = - Аx₀-By₀-Cz₀), называется общим уравнением плоскости. Так, в предыдущем примере уравнению можно придать вид 2x+5y-z+4=0.

Замечание. Всякое уравнение вида (19) (где хотя бы одно из чиселА, В, С не равно нулю) задает плоскость в пространстве и, наоборот, уравнение любой плоскости есть уравнение первой степени.

Отметим, что уравнение ( 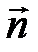, 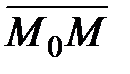)=0 можно применить для вывода уравнения плоскости в пространстве, заданной тремя точками M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂), M₃(x₃,y₃,z₃), не лежащими на одной прямой. Так, взяв в качестве нормального вектора 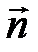= 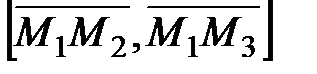- векторное произведение 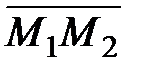на 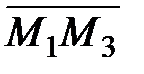, а в качестве M₀ точку M₁, получим

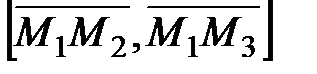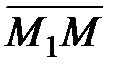( , ) = 0,

что приводит к уравнению плоскости в форме определителя:

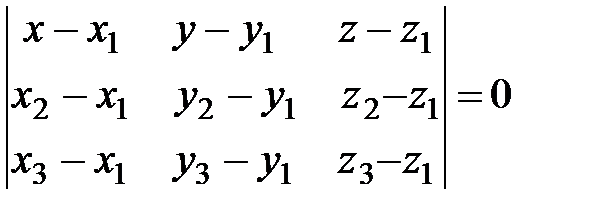. (20)

В частности, если плоскость не проходит через начало координат и пересекает координатные оси в точках M₁ (a,0,0), M₂ (0,b,0), M₃ (0,0,c), то уравнение (20) приводится к виду

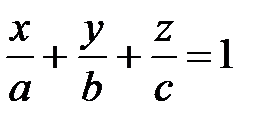, (21)

называемомууравнением плоскости «в отрезках».

Рассмотрим далее частные случаи общего уравнения плоскости.

ЕслиD=0, то уравнение Аx+By+Cz=0 определяет плоскость, проходящую через начало координат. Другие частные случаи определяются расположением нормального вектора 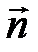= (А,B,C). Так, например, еслиА=0, то уравнение By+Cz+D=0 определяет плоскость, параллельную оси Ox (и проходящую через осьOx, если D=0); если А=B=0, то уравнение Cz+D=0 определяет плоскость, параллельную плоскости Oxy (в частности, z = 0 - уравнение самой плоскости Oxy).

Двугранный угол между двумя плоскостями, заданными своими общими уравнениями

А₁x + B₁y + C₁z + D₁ = 0,

А₂x + B₂y + C₂z + D₂ = 0, (22)

равен углу j между их нормальными векторами 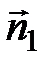=(А₁,B₁,C₁) и 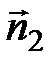= =(А₂,B₂,C₂) и определяется по формуле

cosj = 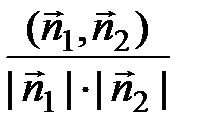= 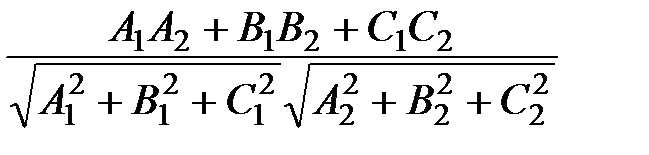; (23)

угол j лежит в пределах от 0 до p; другой двугранный угол, образованный двумя пересекающимися плоскостями, равен p-j.

Пример 17. Найти угол между плоскостями, заданными уравнениями 3x-y-2z+250=0 и x-2y+z-111=0.

Решение. Находим косинус угла между нормальными векторами 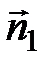=(3,-1,-2) и 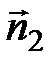=(1,-2,1):

cosj = = ;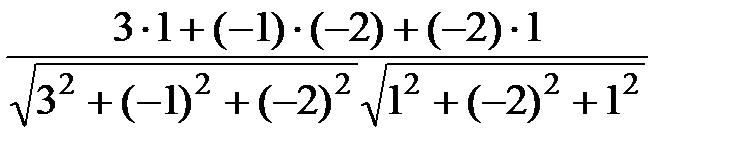

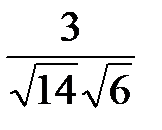отсюда j=arccos 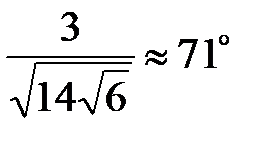. Другой двугранный угол равен 180°-71°=109°. ■

Две данные плоскости (22) перпендикулярны тогда и только тогда, когда их нормальные векторы 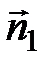=(А₁,B₁,C₁) и 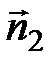=(А₂,B₂,C₂) перпендикулярны между собой, откуда скалярное произведение ( 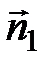, 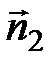)=0 или 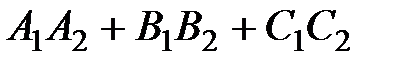=0. Например, плоскости 3x-y+2z-31=0 и 5x+3y-6z+1=0 перпендикулярны, так как 3×5+(-1) ×3+2×(-6)=0. Две данные плоскости параллельны тогда и только тогда, когда их нормальные векторы 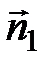и 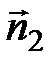коллинеарны, т.е. при выполнении условия .

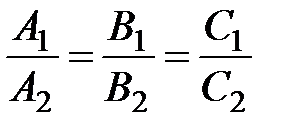Пример 18. Составить уравнение плоскости, проходящей через точку M₀(1,-1,0) и параллельной плоскости 2x+3y-4z-1=0.

Решение. Так как у параллельных плоскостей один и тот же нормальный вектор 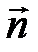=(2,3,-4), то искомое уравнение имеет вид 2(x-1)+3(y+1)-4(z-0)=0 или 2x+3y-4z+1=0. ■

3.3 [кроме ФЭУ] .Прямая линия в пространстве.

Линия в пространстве определяется совместным заданием двух уравнений F(x,y,z)=0, F(x,y,z)=0 как пересечение двух поверхностей, задаваемых этими уравнениями.

Так, прямая в пространствеможет быть задана как линия пересечения двух плоскостей, т.е. как множество точек, удовлетворяющих системе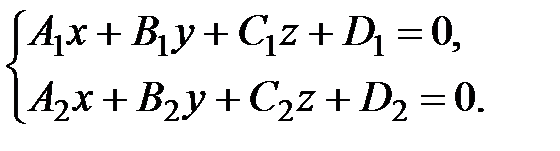

Если прямая в пространстве параллельна вектору 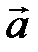= (а₁, а₂, а₃) (называемому направляющим вектором) и проходит через точку M₀(x₀,y₀,z₀), то её уравнения могут быть получены из условия коллинеарности векторов 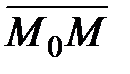= (x-x₀, y-y₀, z-z₀) (где M(x,y,z) - произвольная точка прямой) и 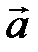= (а₁, а₂, а₃):

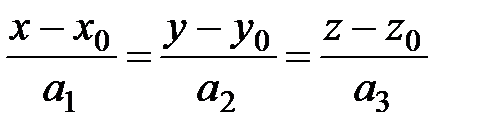. (24)

Уравнения (24) называются каноническими уравнениями прямой в пространстве.

Пример 19.Составить уравнения прямой, проходящей через точки M₀(1,-1,3) и M₁(0,3,5).

Решение. Воспользуемся уравнениями (24), взяв в качестве направляющего вектора 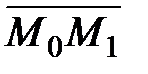= (0-1,3-(-1),5-3) или 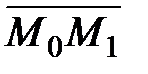= (-1,4,2):

.

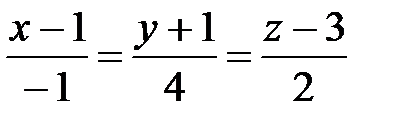Понятие множества

При изложении теории множеств мы будем придерживаться так называемой интуитивной точки зрения, согласно которой такие понятия, как "множество", "элемент множества", относятся к начальным понятиям математики и поэтому не подлежат определению.

С понятием множества мы соприкасаемся, прежде всего тогда, когда по какой-либо причине объединяем по некоторому признаку в одну группу какие-то объекты и далее рассматриваем эту группу или совокупность как единое целое.

Множества принято обозначать заглавными латинскими буквами. Объекты, которые образуют множество, называют элементами множества и для обозначения элементов используют, как правило, малые буквы латинского алфавита. Если a является элементом множества M, то будем говорить, что a принадлежит множеству M, и использовать запись a Î M, в противном случае, если a не принадлежит множеству M, будем использовать обозначение a Ï M.

В различных приложениях дискретной математики чаще всего встречаются конечные множества. Интуитивный смысл этого термина ясен: такие множества содержат конечное число элементов. Число элементов конечного множества A называют мощностью этого множества и обозначают символом Card A или |A|. Наряду с конечными множествами в математике рассматривают и бесконечные множества, то есть такие, которые содержат бесконечно много элементов. Так, например, бесконечно множество натуральных чисел N, множество рациональных чисел Q, множество действительных чисел R.

Способы задания множеств

Множество может быть задано перечислением всех его элементов или списком. В этом случае элементы множества записывают внутри фигурных скобок, например: А = { 1, 2, a, x } или B = { река Нил, город Москва, планета Уран}.

Множество может быть задано описанием свойств его элементов. Чаще всего при этом используют запись A = { x|P( x ) }, которую читают следующим образом: "A есть множество элементов x таких, что для них выполняется свойство P( x )".

Например, B = { x| x- натуральное число, меньшее 10 }, при этом, очевидно, B = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }.

Множество можно задать порождающей процедурой, например:

D = { z |1Î D,и если z Î D,то z + 3 Î D},

E = { x | x = 3^k, k любое нартуральное число.}

Наряду с порождающей процедурой существует распознающая или разрешающая процедура, которая позволяет определить, принадлежит ли данный объект множеству или нет. Для множества D распознающая процедура заключается в том, что для любого натурального числа n будут проверять, является ли число 3 делителем числа n - 1. Для множества E распознающая процедура заключается в разложении числа на простые множители.