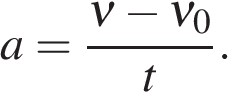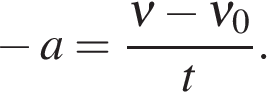Равнопеременное движение по прямой.
Равнопеременное движение по прямой.
3.1.1. Равнопеременное движение по прямой — движение по прямой с постоянным по модулю и направлению ускорением: 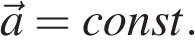
3.1.2. Ускорение ( 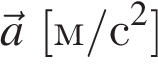 ) — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.
) — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.
В векторном виде:

где  — начальная скорость тела,
— начальная скорость тела,  — скорость тела в момент времени t.
— скорость тела в момент времени t.
В проекции на ось Ox:

где  — проекция начальной скорости на ось Ox,
— проекция начальной скорости на ось Ox,  — проекция скорости тела на ось Ox в момент времени t.
— проекция скорости тела на ось Ox в момент времени t.
Знаки проекций зависят от направления векторов и оси Ox.

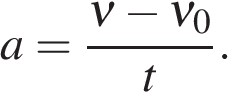

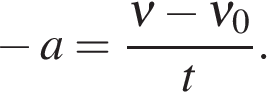
График проекции ускорения от времени.
При равнопеременном движении ускорение постоянно, поэтому будет представлять собой прямые линии, параллельные оси времени (см. рис.):
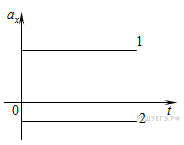
Значение ускорения: чем дальше от оси времени лежит прямая, тем больше модуль ускорения 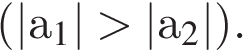
Скорость при равнопеременном движении.
В векторном виде:
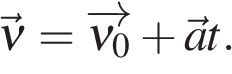
В проекции на ось Ox:
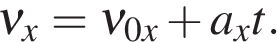
Для равноускоренного движения:

Для равнозамедленного движения:

График проекции скорости в зависимости от времени.
График проекции скорости от времени — прямая линия.
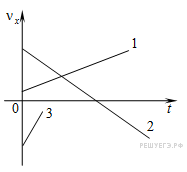
Направление движения: если график (или часть его) находятся над осью времени, то тело движется в положительном направлении оси Ox.
Значение ускорения: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль ускорения; 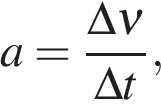 где
где 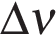 — изменение скорости за время
— изменение скорости за время 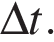
Пересечение с осью времени: если график пересекает ось времени, то до точки пересечения тело тормозило (равнозамедленное движение), а после точки пересечения начало разгоняться в противоположную сторону (равноускоренное движение).
3.1.6. Геометрический смысл площади под графиком в осях 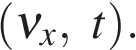
Площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время — это путь, пройденный телом.
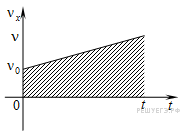
На рис. 3.5 нарисован случай равноускоренного движения. Путь в данном случае будет равен площади трапеции:
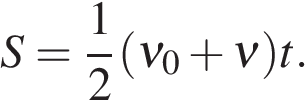 (3.9)
(3.9)
Формулы для расчета пути
Равноускоренное движение  | Равнозамедленное движение  |
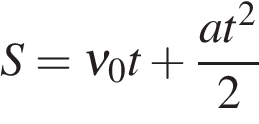 (3.10) (3.10) | 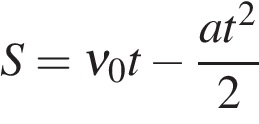 (3.12) (3.12) |
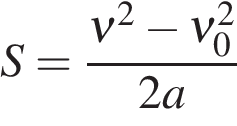 (3.11) (3.11) | 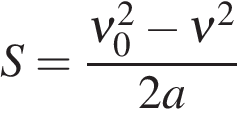 (3.13) (3.13) |
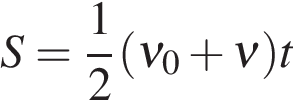 (3.14) (3.14) |
Все формулы, представленные в таблице, работают только при сохранении направления движения, то есть до пересечения прямой с осью времени на графике зависимости проекции скорости от времени.
Если же пересечение произошло, то движение проще разбить на два этапа:
до пересечения (торможение):
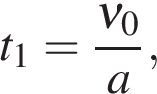

После пересечения (разгон, движение в обратную сторону)

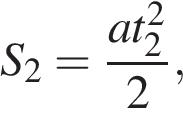
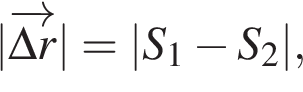
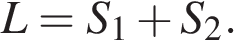
В формулах выше — время от начала движения до пересечения с осью времени (время до остановки), 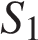 — путь, который прошло тело от начала движения до пересечения с осью времени,
— путь, который прошло тело от начала движения до пересечения с осью времени, 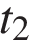 — время, прошедшее с момента пересечения оси времени до данного момента t,
— время, прошедшее с момента пересечения оси времени до данного момента t,  — путь, который прошло тело в обратном направлении за время, прошедшее с момента пересечения оси времени до данного момента t,
— путь, который прошло тело в обратном направлении за время, прошедшее с момента пересечения оси времени до данного момента t,  — модуль вектора перемещения за все время движения, L — путь, пройденный телом за все время движения.
— модуль вектора перемещения за все время движения, L — путь, пройденный телом за все время движения.
Перемещение за -ую секунду.
За время 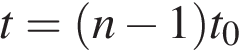 тело пройдет путь:
тело пройдет путь:
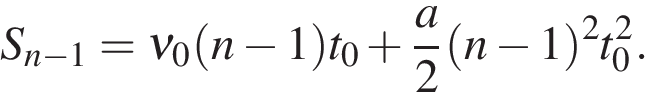
За время  тело пройдет путь:
тело пройдет путь:

Тогда за -ый промежуток 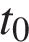 тело пройдет путь:
тело пройдет путь:

За промежуток 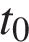 можно принимать любой отрезок времени. Чаще всего
можно принимать любой отрезок времени. Чаще всего  с.
с.
Если  то
то
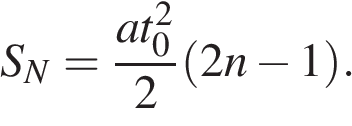
Тогда за 1-ую секунду тело проходит путь:
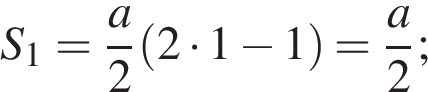
За 2-ую секунду:
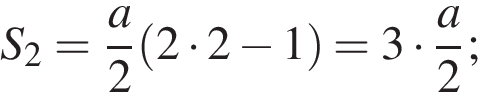
За 3-ю секунду:
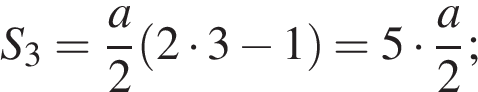
и т. д.
Если внимательно посмотрим, то увидим, что  и т. д.
и т. д.
Таким образом, приходим к формуле:
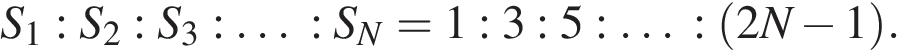
Словами: пути, проходимые телом за последовательные промежутки времени соотносятся между собой как ряд нечетных чисел, и это не зависит от того, с каким ускорением движется тело. Подчеркнем, что это соотношение справедливо при 
Свободное падение тела
Под свободным падением подразумевается следующая физическая модель:
1) Падение происходит под действием силы тяжести:
2) Сопротивление воздуха отсутствует (в задачах иногда пишут «сопротивлением воздуха пренебречь»);
3) Все тела, независимо от массы падают с одинаковым ускорением (иногда добавляют — «независимо от формы тела», но мы рассматриваем движение только материальной точки, поэтому форма тела уже не учитывается);
4) Ускорение свободного падения направлено строго вниз и на поверхности Земли равно 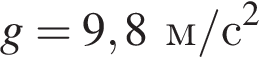 (в задачах часто принимаем
(в задачах часто принимаем  для удобства подсчетов);
для удобства подсчетов);
3.3.1. Уравнения движения в проекции на ось Oy
В отличии от движения по горизонтальной прямой, когда далеко не всех задач происходит смена направления движения, при свободном падении лучше всего сразу пользоваться уравнениями, записанными в проекциях на ось Oy.
Уравнение координаты тела:
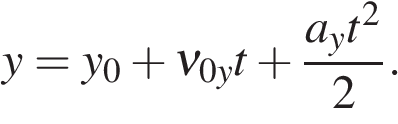
Уравнение проекции скорости:

Как правило, в задачах удобно выбрать ось Oy следующим образом:
Ось Oy направлена вертикально вверх;
Начало координат совпадает с уровнем Земли или самой нижней точкой траектории.
При таком выборе уравнения 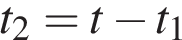 и
и 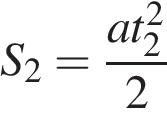 перепишутся в следующем виде:
перепишутся в следующем виде:
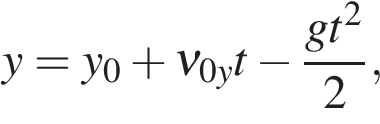

3.4. Движение в плоскости Oxy.
Мы рассмотрели движение тела с ускорением вдоль прямой. Однако этим равнопеременное движение не ограничивается. Например, тело, брошенное под углом к горизонту. В таких задачах необходимо учитывать движение сразу по двум осям:
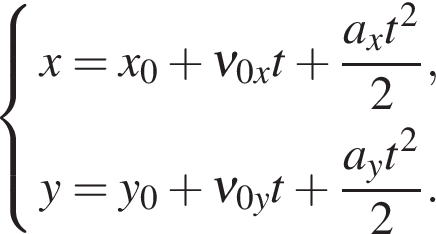
Или в векторном виде:
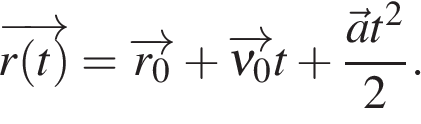
И изменение проекции скорости на обе оси:
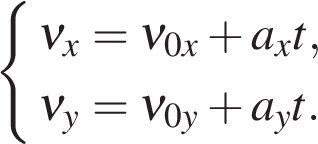
Треугольник скоростей
В векторном виде при постоянном ускорении закон изменения скорости имеет вид (3.5):
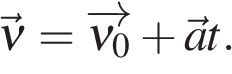
Эта формула означает, что вектор  равен векторной сумме векторов
равен векторной сумме векторов  и
и  Векторную сумму всегда можно изобразить на рисунке (см. рис.).
Векторную сумму всегда можно изобразить на рисунке (см. рис.).
В каждой задаче, в зависимости от условий, треугольник скоростей будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.
Треугольник перемещений
В векторном виде закон движения при постоянном ускорении имеет вид:
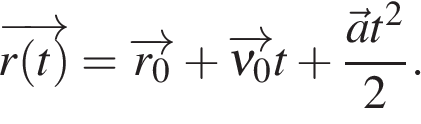
При решении задачи можно выбирать систему отсчета наиболее удобным образом, поэтому не теряя общности, можем выбрать систему отсчета так, что  то есть начало системы координат помещаем в точку, где в начальный момент находится тело. Тогда
то есть начало системы координат помещаем в точку, где в начальный момент находится тело. Тогда
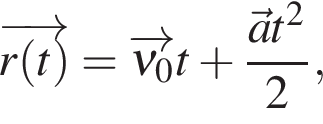
то есть вектор 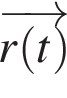 равен векторной сумме векторов
равен векторной сумме векторов  и
и 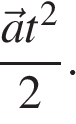 Изобразим на рисунке (см. рис.).
Изобразим на рисунке (см. рис.).
Как и в предыдущем случае в зависимости от условий треугольник перемещений будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.
Равнопеременное движение по прямой.
3.1.1. Равнопеременное движение по прямой — движение по прямой с постоянным по модулю и направлению ускорением: 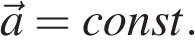
3.1.2. Ускорение ( 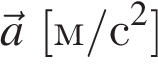 ) — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.
) — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.
В векторном виде:

где  — начальная скорость тела,
— начальная скорость тела,  — скорость тела в момент времени t.
— скорость тела в момент времени t.
В проекции на ось Ox:

где  — проекция начальной скорости на ось Ox,
— проекция начальной скорости на ось Ox,  — проекция скорости тела на ось Ox в момент времени t.
— проекция скорости тела на ось Ox в момент времени t.
Знаки проекций зависят от направления векторов и оси Ox.