Теплопроводность при стационарном режиме
При установившемся тепловом режиме температура тела не изменяется с течением времени, поэтому в уравнении (2.5) производная  . Распределение температуры в теле описывается уравнением (2.6). Решение такого уравнения сопряжено со значительными трудностями.
. Распределение температуры в теле описывается уравнением (2.6). Решение такого уравнения сопряжено со значительными трудностями.
Рассмотрим теплопроводность в телах простейшей формы, которые позволяют получить точные решения уравнения теплопроводности.
4.1. Теплопроводность плоской стенки
Рассмотрим плоскую стенку, высота и ширина которой значительно больше её толщины. В этом случае такую стенку можно считать бесконечной (рис. 5). Тепло будет передаваться только в одном направлении – вдоль оси х. Если считать, что теплопроводность стенки величина постоянная, то уравнение теплопроводности в
 Рис.5. Плоская стенка Рис.5. Плоская стенка | этом случае можно записать в виде  . (4.1) Решение (4.1) имеет вид . (4.1) Решение (4.1) имеет вид  , где С1 и С2 – постоянные. Для их определения нужно задать два граничных условия. а) граничные условия первого рода при х=0 , где С1 и С2 – постоянные. Для их определения нужно задать два граничных условия. а) граничные условия первого рода при х=0  ; при ; при   . . |
Получим два уравнения для определения С1 и С2
 и
и  ,
,
из которых найдём  и
и  . Таким образом,
. Таким образом,
 . (4.2)
. (4.2)
Количество тепла, проходящего через стенку, определим по закону Фурье.
 . (4.3)
. (4.3)
Разность температур  называется температурным напором, а
называется температурным напором, а  – термическим сопротивлением теплопроводности плоской стенки, м2град/Вт.
– термическим сопротивлением теплопроводности плоской стенки, м2град/Вт.
Из формулы (4.2) следует, что распределение температуры в плоской стенке представляет собой прямую линию, а из (4.3) следует, что плотность теплового потока через плоскую стенку не зависит от координаты х.
Рассмотрим теплопроводность многослойной плоской стенки, состоящей из n слоёв различной толщины  из разных материалов с разной теплопроводностью
из разных материалов с разной теплопроводностью  . При стационарном тепловом режиме тепловой поток одинаков в каждом слое.
. При стационарном тепловом режиме тепловой поток одинаков в каждом слое.
 Рис.6. Многослойная плоская стенка Рис.6. Многослойная плоская стенка |  ; ;  ; ………………… ; …………………  . Из этих уравнений найдём температурные напоры в каждом слое. . Из этих уравнений найдём температурные напоры в каждом слое. |
 ;
;
 ;
;
……………….
 .
.
Сложив уравнения, получим
 .
.
откуда
 .
.
б) граничные условия третьего рода
 Рис. 7. Граничные условия третьего рода Рис. 7. Граничные условия третьего рода | Передача тепла от одной жидкости к другой через разделяющую их стенку называется теплопередачей. Расчётная схема приведена на рис.7. С одной стороны стенки находится жидкость с температурой  , с другой стороны – жидкость с температурой , с другой стороны – жидкость с температурой  . Примем для определённости, что . Примем для определённости, что  > >  . Перенос тепла между жидкостями и стенкой рассчитывается по формуле Ньютона – Рихмана. Будем считать коэффициенты теплоотдачи постоянными и не завися- . Перенос тепла между жидкостями и стенкой рассчитывается по формуле Ньютона – Рихмана. Будем считать коэффициенты теплоотдачи постоянными и не завися- |
щими от температуры. В соответствии с формулой Ньютона тепловой поток между жидкостью и левой стороной стенки определяется как
 . (а)
. (а)
В стационарных условиях этот же тепловой поток пройдёт через стенку и передастся к другой жидкости.
 ; (б)
; (б)
 . (в)
. (в)
Найдём из (а) – (в) разности температур, сложим получившиеся выражения и найдём q.
 . (4.4)
. (4.4)
Обозначим
 .
.
Тогда (4.4) можно переписать в виде
 .
.
Величина k называется коэффициентом теплопередачи и имеет ту же размерность, как и коэффициент теплоотдачи, Вт/м2К. Величина обратная k называется полным термическим сопротивлением теплопередачи
 ,
,
а отношение  называется термическим сопротивлением теплоотдачи.
называется термическим сопротивлением теплоотдачи.
Общее термическое сопротивление равно сумме частных сопротивлений, поэтому для многослойной стенки полное термическое сопротивление можно записать в виде

и плотность теплового потока в случае многослойной стенки запишем в виде
 .
.
Температуры на поверхностях стенки  и
и  найдём из (а) и (в)
найдём из (а) и (в)
 ;
;
 .
.
Температура на границе слоёв i и i+1 можно найти следующим образом
 .
.
4.2. Теплопроводность цилиндрической стенки
     Рис.8. Расчётная схема Рис.8. Расчётная схема |
Перенос тепла в цилиндре описывается уравнением теплопроводности в цилиндрических координатах – r,  , z (см. рис.8).
, z (см. рис.8).
 . (4.5)
. (4.5)
Если коэффициент теплопроводности не зависит от температуры и при отсутствии источников внутреннего тепловыделения уравнение (4.5) можно упростить.
 .
.
Если цилиндр находится в среде, температура которой по окружности цилиндра постоянна, то вдоль координаты  переноса тепла не будет, поскольку в этом направлении
переноса тепла не будет, поскольку в этом направлении  . Если длина цилиндра стремится к бесконечности, то перенос тепла вдоль оси z также равен нулю. В таком цилиндре изотермические поверхности будут представлять соосные цилиндры (см. рис.8) и перенос тепла будет происходить только в направлении радиуса r. В стационарном тепловом режиме температура не зависит от времени и будет изменяться только по радиусу цилиндра. В результате уравнение примет вид
. Если длина цилиндра стремится к бесконечности, то перенос тепла вдоль оси z также равен нулю. В таком цилиндре изотермические поверхности будут представлять соосные цилиндры (см. рис.8) и перенос тепла будет происходить только в направлении радиуса r. В стационарном тепловом режиме температура не зависит от времени и будет изменяться только по радиусу цилиндра. В результате уравнение примет вид
 . (4.6)
. (4.6)
Рассмотрим процесс переноса тепла в цилиндрической стенке (трубе) с внутренним диаметром  и наружным диаметром
и наружным диаметром  (см. рис.9). Обозначим
(см. рис.9). Обозначим  . Уравнение примет вид
. Уравнение примет вид
 . (4.7)
. (4.7)
Интегрируя (4.7) получим

или
 и
и  . Заменяя u на dt/dr получим
. Заменяя u на dt/dr получим
 .
.
После интегрирования найдём
 .
.
Для определения постоянных С1 и С2 необходимо задать граничные условия.
а) граничные условия первого рода
 Рис.9. Теплопроводность цилиндрической стенки Рис.9. Теплопроводность цилиндрической стенки | В этом случае при r=R1  и при r=R2 и при r=R2  . .  ; ;  . Отсюда . Отсюда  ; ;  . Таким образом, решение данной задачи имеет вид . Таким образом, решение данной задачи имеет вид  . . |
или
 . (4.8)
. (4.8)
Как следует из (4.8), распределение температуры внутри цилиндрической стенки представляет собой логарифмическую кривую. Найдём плотность теплового потока.
 , Вт/м2.
, Вт/м2.
Таким образом, для цилиндрической стенки плотность теплового потока через любую изотермическую поверхность зависит от радиуса (диаметра). Тепловой поток через цилиндрическую поверхность  равен
равен
 , Вт.
, Вт.
Для единицы длины изотермической поверхности
 , Вт/м.
, Вт/м.
Тепловой поток, отнесённый к единице длины поверхности, называется линейной плотностью теплового потока –  . Таким образом,
. Таким образом,  , где
, где  и
и  плотности теплового потока на поверхностях диаметра
плотности теплового потока на поверхностях диаметра  и
и  . Отсюда следует связь между линейной плотностью теплового потока и плотностями теплового потока.
. Отсюда следует связь между линейной плотностью теплового потока и плотностями теплового потока.
 ;
;  .
.
Величина  , мК/Вт называется линейным термическим сопротивлением теплопроводности цилиндрической стенки. В случае многослойной цилиндри-
, мК/Вт называется линейным термическим сопротивлением теплопроводности цилиндрической стенки. В случае многослойной цилиндри-
 Рис.10. Многослойная цилиндрическая стенка Рис.10. Многослойная цилиндрическая стенка | ческой стенки (рис.10) линейное термическое сопротивление равно сумме термических сопротивлений слоёв и линейная плотность теплового потока равна  . Температура на границе любого слоя есть . Температура на границе любого слоя есть  . . |
б) граничные условия третьего рода
 Рис.11. цилиндрическая стенка Рис.11. цилиндрическая стенка | Будем считать, что цилиндр бесконечно длинный, поэтому можно пренебречь потерями тепла с торцов. Температуры жидкостей внутри и снаружи трубы, а также коэффициенты теплоотдачи постоянны. В таком случае тепло будет передаваться только по радиусу. В стационарном случае количество тепла, переданное от одной жидкости к стенке равно количеству тепла переносимо- |
го теплопроводностью через стенку и равно количеству тепла, воспринятому другой жидкостью. Для единицы длины поверхности можно записать
 (4.9)
(4.9)
Выразим из (4.9) разности температур и сложим получившиеся уравнения.

и определим
 ,
,
где  называется линейным коэффициентом теплопередачи
называется линейным коэффициентом теплопередачи
 .
.
Величина  называется линейным термическим сопротивлением теплоотдачи. Для многослойной цилиндрической стенки
называется линейным термическим сопротивлением теплоотдачи. Для многослойной цилиндрической стенки
 .
.
4.3. Критический диаметр цилиндрической стенки
 Рис. 12. К критическому диаметру изоляции Рис. 12. К критическому диаметру изоляции | Рассмотрим трубу, диаметром  , покрытую слоем тепловой изоляции , покрытую слоем тепловой изоляции  (см. рис.12). Выясним влияние диаметра изоляции на термическое сопротивление всей системы. Запишем термическое сопротивление системы труба-изоляция. (см. рис.12). Выясним влияние диаметра изоляции на термическое сопротивление всей системы. Запишем термическое сопротивление системы труба-изоляция.  (4.10) Построим график изменения Rl в зависимости от диаметра изоляции. Обозначим (4.10) Построим график изменения Rl в зависимости от диаметра изоляции. Обозначим  ; ;  ; ;  Построим графики изменения термических сопротивлений в зависимости от диаметра изоляции (см. рис.13). Как следует из рис. 13, при некотором Построим графики изменения термических сопротивлений в зависимости от диаметра изоляции (см. рис.13). Как следует из рис. 13, при некотором |
значении  , термическое сопротивление системы имеет минимум, а тепловые потери – максимум (рис.14). Для определения значения
, термическое сопротивление системы имеет минимум, а тепловые потери – максимум (рис.14). Для определения значения  исследуем (4.10) на экстремум.
исследуем (4.10) на экстремум.
 Рис.13. Зависимость термических сопротивлений от диаметра изоляции Рис.13. Зависимость термических сопротивлений от диаметра изоляции |  Рис. 14. Зависимость тепловых потерь от диаметра изоляции Рис. 14. Зависимость тепловых потерь от диаметра изоляции |
 .
.
Отсюда
 .
.
Если  , то с ростом диаметра изоляции тепловые потери растут и достигают максимального значения при
, то с ростом диаметра изоляции тепловые потери растут и достигают максимального значения при  . Затем при дальнейшем увеличении
. Затем при дальнейшем увеличении  потери тепла начинают уменьшаться и при
потери тепла начинают уменьшаться и при  потери тепла становятся равным потерям неизолированной трубы и только при
потери тепла становятся равным потерям неизолированной трубы и только при  потери тепла начинают уменьшаться. Таким образом слой изоляции толщиной
потери тепла начинают уменьшаться. Таким образом слой изоляции толщиной  не выполнял функции тепловой изоляции.
не выполнял функции тепловой изоляции.
Следовательно, критический диаметр изоляции должен быть меньше наружного диаметра изолируемой трубы, т.е.  . В этом случае слой изоляции сразу же будет уменьшать тепловые потери. Найдём допустимую величину коэффициента теплопроводности изоляционного материала, положив
. В этом случае слой изоляции сразу же будет уменьшать тепловые потери. Найдём допустимую величину коэффициента теплопроводности изоляционного материала, положив  .
.
 .
.
4.4. Передача тепла через шаровую стенку
Поле температур в шаре описывается уравнением теплопроводности в сферических координатах. Связь сферических и декартовых координат задаётся соотношениями
 ;
;
 ;
;
 .
.
 Рис. 15. К шаровой стенке Рис. 15. К шаровой стенке | Уравнение теплопроводности в сферических координатах имеет следующий вид.  Пусть имеется полый шар с радиусами Пусть имеется полый шар с радиусами  и и  . Если температура на поверхностях шара одинакова во всех точках поверхностей, перенос тепла будет происходить только в направлении радиуса. В стационарном тепловом режиме при постоянном коэффициенте теплопроводности уравнение можно упростить. . Если температура на поверхностях шара одинакова во всех точках поверхностей, перенос тепла будет происходить только в направлении радиуса. В стационарном тепловом режиме при постоянном коэффициенте теплопроводности уравнение можно упростить. |

или
 . (4.11)
. (4.11)
Обозначив  преобразуем (4.11) к виду
преобразуем (4.11) к виду
 .
.
Решение имеет вид
 .
.
Заменяя u получим уравнение

интегрируя которое получим общее решение уравнения.
 . (4.12)
. (4.12)
а) граничные условия первого рода
При 
 ; при
; при 
 ,
,  . Для определения постоянных
. Для определения постоянных  и
и  получим два уравнения.
получим два уравнения.
 ;
; 
из которых найдём
 ;
;  .
.
Распределение температуры в шаровой стенке есть
 .
.
Тепловой поток через шаровую стенку равен
 .
.
б) граничные условия третьего рода
При 
 – тепло, которое передаётся от первой жидкости к стенке.
– тепло, которое передаётся от первой жидкости к стенке.
 – тепло, которое переносится теплопроводностью через стенку;
– тепло, которое переносится теплопроводностью через стенку;
При 
 – тепло, которое передаётся от стенки ко второй жидкости.
– тепло, которое передаётся от стенки ко второй жидкости.
Таким образом
 .
.
4.5. Теплопроводность стержня постоянного поперечного сечения
 Рис. 16. Теплопроводность стержня Рис. 16. Теплопроводность стержня | Будем считать стержнем тело, длина которого намного больше двух других размеров. Форма сечения может быть любой, таким образом сечение характеризуется площадью сечения f и периметром сечения u. Будем считать, что коэффициент теплопроводности стержня достаточно велик, так что можно считать, что температура стержня в сечении изменяется незначительно и её изменением можно пренебречь. Стержень находится в среде с постоянной температурой. Коэффициент теплоотдачи между стержнем и средой будем считать постоянным по длине стержня. |
Таким образом, при данных предположениях температура стержня будет изменяться только по длине.
Рассмотрим элемент стержня длиной dx (см. рис. 16) и запишем для него уравнение баланса тепла.
 . (а)
. (а)
 и
и  .
.
По закону Фурье  и
и  . (б)
. (б)
С другой стороны, количество тепла, поступающего из стержня через поверхность элемента dx есть (предполагается, что температура стержня больше температуры окружающей среды)
 , (в)
, (в)
где  – избыточная температура. Приравнивая (б) и (в), получим дифференциальное уравнение
– избыточная температура. Приравнивая (б) и (в), получим дифференциальное уравнение
 (4.13)
(4.13)
где  . Решение уравнения (4.13) записывается в виде
. Решение уравнения (4.13) записывается в виде
 .
.
Постоянные интегрирования  и
и  определяются при помощи граничных условий. Рассмотрим случай, когда в начальном сечении можно поддерживать постоянной температуру стержня, т.е. граничное условие при x=0 можно задать в виде
определяются при помощи граничных условий. Рассмотрим случай, когда в начальном сечении можно поддерживать постоянной температуру стержня, т.е. граничное условие при x=0 можно задать в виде  или
или  . Граничное условие на другом конце стержня можно задать различными способами.
. Граничное условие на другом конце стержня можно задать различными способами.
а) стержень бесконечной длины
Если стержень достаточно длинный, то температура на его конце будет мало отличаться от температуры окружающей среды, что точно выполняется, если длина стержня  . В этом случае второе граничное условие можно записать в виде: при
. В этом случае второе граничное условие можно записать в виде: при 
 . Получим два уравнения для определения
. Получим два уравнения для определения  и
и  .
.
 и
и  .
.
Отсюда  и
и  , и распределение температуры по длине стержня имеет следующий вид.
, и распределение температуры по длине стержня имеет следующий вид.
 .
.
Количество тепла, которое стержень передаёт в окружающую среду проходит через сечение х=0. Поэтому его можно определить как
 .
.
б) стержень конечной длины
В этом случае граничное условие при x=l может быть задано в следующем виде
 ,
,
где  – коэффициент теплоотдачи на торце стержня. Если площадь сечения стержня намного меньше площади его боковой поверхности, то теплоотдачей с торца стержня можно пренебречь. В этом случае граничное условие при x=l запишется в виде
– коэффициент теплоотдачи на торце стержня. Если площадь сечения стержня намного меньше площади его боковой поверхности, то теплоотдачей с торца стержня можно пренебречь. В этом случае граничное условие при x=l запишется в виде
 .
.
Для определения постоянных  и
и  получим два уравнения
получим два уравнения
 ;
;
 .
.
Отсюда найдём
 ;
;  .
.
Таким образом, распределение температуры по длине стержня есть
 .
.
Умножим и разделим правую часть на  .
.
 .
.
Количество тепла, отдаваемое поверхностью стержня равно
 . (4.14)
. (4.14)
Если теплоотдачей с торца стержня нельзя пренебречь, то распределение температуры по длине стержня есть
 .
.
Количество тепла, отдаваемое стержнем
 .
.
4.7. Теплопередача через ребристую плоскую стенку
Оребрение применяется для увеличения площади поверхности теплообмена с целью увеличения количества передаваемого тепла. При этом рёбра располагаются с той стороны стенки, на которой меньше коэффициент теплоотдачи.
Ребристая стенка обтекается жидкостями (см. рис. 17) с температурой  и коэффициентом теплоотдачи
и коэффициентом теплоотдачи  с одной стороны и температурой
с одной стороны и температурой  и коэффициен-
и коэффициен-
 Рис.17. Ребристая плоская стенка Рис.17. Ребристая плоская стенка | том теплоотдачи 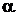 с другой. Для определённости примем с другой. Для определённости примем  > >  и и  > > 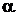 . Необходимо найти тепловой поток через ребристую стенку. Обычно b>> . Необходимо найти тепловой поток через ребристую стенку. Обычно b>>  , поэтому приближённо периметр поперечного сечения ребра u=2(b+ , поэтому приближённо периметр поперечного сечения ребра u=2(b+  )=2b. Площадь сечения есть )=2b. Площадь сечения есть  . Следовательно . Следовательно  . Подставим это выражение в (4.14) и умножим и разделим на 2l. . Подставим это выражение в (4.14) и умножим и разделим на 2l. |
 .
.


или
 .
.
Т.о.
 .
.
Обозначим  – критерий подобия Био. Он представляет собой отношение внутреннего термического сопротивления теплопроводности
– критерий подобия Био. Он представляет собой отношение внутреннего термического сопротивления теплопроводности  к внешнему термическому сопротивлению теплоотдачи
к внешнему термическому сопротивлению теплоотдачи  , т.е.
, т.е.  . Окончательно
. Окончательно
 . (4.15)
. (4.15)
В (4.15)  – площадь боковой поверхности ребра.
– площадь боковой поверхности ребра.
Обозначим  – коэффициент эффективности ребра. Тогда (4.15) принимает вид
– коэффициент эффективности ребра. Тогда (4.15) принимает вид
 .
.
Тепло, отдаваемое гладкой частью оребрённой поверхности, т.е. поверхностью, не занятой рёбрами есть  , где
, где  – коэффициент теплоотдачи от гладкой части стенки. Таким образом, общее количество тепла со стороны оребрённой поверхности есть
– коэффициент теплоотдачи от гладкой части стенки. Таким образом, общее количество тепла со стороны оребрённой поверхности есть
 +
+ 
или
 ,
,
где
 .
.
Здесь  называется приведённым коэффициентом теплоотдачи. Количество тепла, передаваемого к неоребрённой стенке есть
называется приведённым коэффициентом теплоотдачи. Количество тепла, передаваемого к неоребрённой стенке есть
 .
.
Через стенку теплопроводностью передаётся количество тепла
 .
.
Оребрённая сторона стенки передаёт к второй жидкости количество тепла
 .
.
Из этих уравнений получаем
 .
.
Отношение оребрённой поверхности к гладкой  называется коэффициентом оребрения.
называется коэффициентом оребрения.
4.8. Круглое ребро постоянной толщины
Круглые рёбра применяются при оребрении труб (см. рис. 18). Заданы внутренний радиус ребра  , наружный
, наружный  , толщина ребра
, толщина ребра  и коэффициент теплопроводности
и коэффициент теплопроводности  . Температура окружающей среды равна
. Температура окружающей среды равна 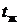 и одинакова вдоль ребра. Температура у основания ребра равна
и одинакова вдоль ребра. Температура у основания ребра равна  . Коэффициент теплоотдачи
. Коэффициент теплоотдачи 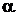 одинаков вдоль всей поверхности ребра.
одинаков вдоль всей поверхности ребра.
 Рис. 18. Круглое ребро постоянной толщины Рис. 18. Круглое ребро постоянной толщины |
Обозначим через  избыточную температуру ребра. Запишем уравнение баланса тепла для кольцевого элемента ребра толщиной dr.
избыточную температуру ребра. Запишем уравнение баланса тепла для кольцевого элемента ребра толщиной dr.
 .
.
 и
и  .
.
 ;
;  .
.
Таким образом, из уравнения баланса получим дифференциальное уравнение теплопроводности для круглого ребра
 . (4.16)
. (4.16)
Обозначим  ; mr=z;
; mr=z;  и подставим в (4.16). Получим уравнение
и подставим в (4.16). Получим уравнение
 ,
,
которое называется уравнением Бесселя. Решение этого уравнения имеет вид
 ,
,
где  – модифицированная функция Бесселя первого рода нулевого порядка мнимого аргумента, а
– модифицированная функция Бесселя первого рода нулевого порядка мнимого аргумента, а  – модифицированная функция Бесселя второго рода нулевого порядка мнимого аргумента.
– модифицированная функция Бесселя второго рода нулевого порядка мнимого аргумента.
 |  |
| Рис. 19 Модифицированные функции Бесселя |
На рис. 19 приведены графики модифицированных функций Бесселя.
При  и
и  ;
;
при  и
и  .
.
Граничные условия задаются аналогично граничным условиям в задаче о прямоугольном ребре, т.е. при 
 ; при
; при 
 . В результате изменение температуры по радиусу определяется как
. В результате изменение температуры по радиусу определяется как
 .
.
Количество тепла равно
 ,
,
где
 .
.
Теплоотдачу с торца ребра можно учесть, условно увеличив радиус ребра  на половину его толщины.
на половину его толщины.
4.9. Теплопроводность пластины с внутренними источниками тепла
 Рис.20. Пластина с внутренними источниками тепла Рис.20. Пластина с внутренними источниками тепла | Тепло в твёрдом теле может выделяться, например, при прохождении электрического тока или в результате химических реакций. Рассмотрим бесконечную пластину толщиной  , которая находится в среде с температурой , которая находится в среде с температурой  . Коэффициент теплоотдачи с обеих сторон одинаков и равен . Коэффициент теплоотдачи с обеих сторон одинаков и равен 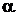 . Источники тепла равномерно распределены по объёму пластины. Будем считать, что теплофизические свойства пластины не зависят от температуры. При данных условиях распределение температуры по толщине пластины будет симметрично относительно середины. Уравнение теплопроводности имеет следующий вид. . Источники тепла равномерно распределены по объёму пластины. Будем считать, что теплофизические свойства пластины не зависят от температуры. При данных условиях распределение температуры по толщине пластины будет симметрично относительно середины. Уравнение теплопроводности имеет следующий вид.  . . |
Граничное условие на поверхности пластины зададим в виде
 .
.
Второе условие задаётся в центре пластины в виде
 .
.
Решение уравнения имеет вид:
 откуда
откуда
 .
.
Постоянные  и
и  находим из граничных условий:
находим из граничных условий:
 , откуда получим
, откуда получим  , и
, и
 , откуда
, откуда  .
.
Таким образом, распределение температуры в пластине есть
 . (4.17)
. (4.17)
Тепловой поток в пластине есть  .
.
Решение (4.17) получено при условии  . При больших перепадах температур в пластине может возникнуть необходимость учесть зависимость
. При больших перепадах температур в пластине может возникнуть необходимость учесть зависимость  от температуры. Во многих случаях с достаточной точностью эту зависимость можно принять линейной
от температуры. Во многих случаях с достаточной точностью эту зависимость можно принять линейной  . Тогда
. Тогда  . После интегрирования получим
. После интегрирования получим  . Постоянную С найдём из условия при х=0
. Постоянную С найдём из условия при х=0  :
:  . Получим распределение температуры в пластине в виде
. Получим распределение температуры в пластине в виде
 .
.
4.10. Теплопроводность цилиндра с внутренними источниками тепла
 Рис. 21. Цилиндр с внутренними источниками тепла Рис. 21. Цилиндр с внутренними источниками тепла | Рассмотрим круглый цилиндр, длина которого намного больше диаметра, который находится в среде с температурой  . Коэффициент теплоотдачи равен . Коэффициент теплоотдачи равен 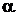 . Источники тепла равномерно распределены по объёму цилиндра. Будем считать, что теплофизические свойства цилиндра не зависят от температуры. При данных условиях распределение температуры по радиусу будет симметрично относительно середины. Уравнение теплопроводности имеет следующий вид. . Источники тепла равномерно распределены по объёму цилиндра. Будем считать, что теплофизические свойства цилиндра не зависят от температуры. При данных условиях распределение температуры по радиусу будет симметрично относительно середины. Уравнение теплопроводности имеет следующий вид.  . . |
Граничные условия:
при r=0 dt/dr=0;
при r=R  .
.
Обозначим  . Получим уравнение
. Получим уравнение
 .
.
Умножим левую и правую части на  . Получим
. Получим
 .
.
Интегрируем
 .
.
Заменим u на  , разделим обе части на r.
, разделим обе части на r.
 .
.
Интегрируем второй раз.
 .
.
Постоянные  и
и  находим из граничных условий.
находим из граничных условий.
 ;
;  .
.
Распределение температуры по радиусу стержня определяется из
 .
.
