Учебное пособие к выполнению расчетно-графических работ

Д.В. Кузьмин

ТЕОРИЯ МЕХАНИЗМОВ И МАШИН

Учебное пособие к выполнению расчетно-графических работ

Северодвинск

УДК 621.01 (075.8)

Кузьмин Д.В. Теория механизмов и машин: учебное пособие к выполнению расчетно-графических работ. – Северодвинск: Севмашвтуз, 2009. – 71 с.

Рецензенты: Зав. каф. «Робототехнические системы, машины и

оборудование лесного компекса» Архангельского

государственного технического университета,

к.т.н., доцент Б.К. Микитюк;

Зав.каф.«Проектирование подъемно-транспортного и технологического оборудования» Севмашвтуза,

к.т.н., доцент А.В. Руденко

Учебное пособие к выполнению расчетно-графических работ по дисциплине «Теория механизмов и машин» состоит из следующих разделов: «Основные теоретические сведения», «Описание механизма по кинематической схеме», «Структурный анализ», «Кинематический анализ», «Силовой анализ», «Указания к оформлению и защите расчетно-графических работ». Целью учебного пособия является оказание помощи студентам в выполнении и подготовке к защите контрольных работ по дисциплине «Теория механизмов и машин». Учебное пособие предназначено для студентов заочной формы обучения, программа профессиональной подготовки которых предусматривает изучение дисциплины «Теория механизмов и машин»

Ил. 45. Табл. 4. Библиогр. 1 назв.

Печатается по решению редакционно-издательского совета Севмашвтуза

ISBN

© Севмашвтуз, 2009 г.

СОДЕРЖАНИЕ

	Стр.

ВВЕДЕНИЕ………..……………………………………………………………..5

1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ………………………..6

1.1. Теория механизмов и машин. Общие сведения……………………..6

1.2. Механизм и его основные характеристики…………………………..7

1.3. Кинематические пары. Схемы механизмов………………………...11

1.4. Классификация механизмов………………………………………….14

1.5. Плоские четырехзвенные рычажные механизмы…………………..16

1.6. Степени свободы механизма. Универсальные структурные

формулы………………………………………………………………18

1.7. Местные подвижности……………………………………………….20

1.8. Избыточные связи…………………………………………………….21

1.9. Принцип строения рычажных механизмов………………………….25

1.10. Структурный анализ механизма……………………………………..28

1.11. Принцип образования рычажных механизмов……………………..28

1.12. Кинематический анализ механизма…………………………………30

1.13. Определение функции положения механизма графическим

методом………………………………………………………………..31

1.14. Определение функции положения механизма аналитическим методом………………………………………………………………..31

1.15. Графическое дифференцирование…………………………………..33

1.16. Метод векторных планов…………………………………………….35

1.17. Характеристики рабочих процессов…………………………………37

1.18. Силовой анализ механизма…………………………………………..38

1.19. Исследование разрешимости задачи силового анализа в общей постановке…………………………………………………………….39

1.20. Способы понижения числа неизвестных сил и моментов…………40

1.21. Реакции в кинематических парах……………………………………41

1.22. Уравнения кинетостатики……………………………………………42

1.23. Теорема Жуковского………………………………………………….43

1.24. Определение обобщенной движущей силы методом Жуковского..44

1. ОПИСАНИЕ РАБОТЫ МЕХАНИЗМА

ПО КИНЕМАТИЧЕСКОЙ СХЕМЕ…………………………………….46

1. СТРУКТУРНЫЙ АНАЛИЗ…………………………………………….47
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ………………………………………49

4.1.Определение функции положения и кинематических

характеристик выходного звена механизма……………………….49

4.2.Построение планов скоростей и ускорений………………………..53

1. СИЛОВОЙ АНАЛИЗ…………………………………………………….56

5.1.Определение неизвестных сил методом векторных планов………56

5.2.Определение движущего момента методом Жуковского………….61

1. УКАЗАНИЯ К ОФОРМЛЕНИЮ И ЗАЩИТЕ

РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ……………………………...62

6.1.Оформление расчетно-пояснительной записки………………….……62

6.2.Оформление графической части………………………………………..63

6.3.Защита проекта…………………………………………………………..64

СПИСОК ЛИТЕРАТУРЫ……………..……………………………………...71

ВВЕДЕНИЕ

Теория механизмов и машин является одной из основных дисциплин в системе подготовки инженеров, способных не только правильно эксплуатировать имеющиеся в наличии машины и технологическое оборудование, но и создавать новые машины, отвечающие всему комплексу требований, обусловленных их целевым назначением.

Настоящее учебное пособие к выполнению расчетно-графических работ по дисциплине «Теория механизмов и машин» предназначено для студентов заочной формы обучения, программы профессиональной подготовки которых предусматривают изучение данной дисциплины. Цель учебного пособия состоит в том, чтобы, с одной стороны, максимально упростить понимание задач, предусмотренных типовыми заданиями на расчетно-графические работы; с другой стороны, оказать помощь студенту в его самостоятельной работе по решению задач и оформлению полученных результатов. Объектом исследования в заданиях на расчетно-графические работы являются плоские шестизвенные рычажные механизмы, которые применяются как исполнительные в составе действующего технологического оборудования. В процессе выполнения расчетно-графических работ студентам предлагается выполнить описание механизма по кинематической схеме, а также его структурный, кинематический и силовой анализ. Самостоятельное выполнение этих инженерных задач позволит будущему специалисту не только усвоить теоретические основы изучаемой дисциплины, но и выработать навыки применения методов анализа механизмов в соответствии с основным принципом проектирования машин – последовательностью.

В учебном пособии приведены краткие теоретические сведения и вопросы для самоконтроля, подробно рассмотрен пример выполнения типового задания, даны методические указания к выполнению, оформлению и защите расчетно-графических работ, приведены темы и варианты заданий. Темы и варианты заданий на расчетно-графические работы разработаны на основе учебных заданий по теории механизмов, опубликованных в [1]. Бланки заданий на расчетно-графические работы приведены в разделе «Указания к оформлению и защите расчетно-графических работ», стр. 66 – 70. Разделы учебного пособия отражают последовательность выполнения учебных заданий.

Классификация механизмов

Механизмы различаются по функциональному назначению, по конструктивному устройству, по расположению в пространстве, по наличию или отсутствию замкнутых кинематических контуров.

По функциональному назначению механизмы подразделяются на исполнительные, передаточные и программные.

· Исполнительные механизмы предназначены для приведения в движение рабочих органов машины в соответствии с выполняемым технологическим процессом.

· Передаточные механизмы служат для преобразования механической энергии двигателей в механическую энергию с параметрами, требуемыми для приведения в движение входных звеньев исполнительного механизма.

· Программные механизмы задают программу движения механической части машины.

Пример

Рассмотрим транспортную машину – автомобиль. Рабочими органами автомобиля являются колеса. Исполнительный механизм – шасси. Коробка передач – многоступенчатый передаточный механизм, необходимый для согласования работы двигателя и шасси в различных режимах движения машины. Двигатель автомобиля содержит газораспределительный механизм, который является программным (он управляет движением впускных и выпускных клапанов двигателя).

По конструктивному устройству различают рычажные, зубчатые, кулачковые и фрикционные механизмы.

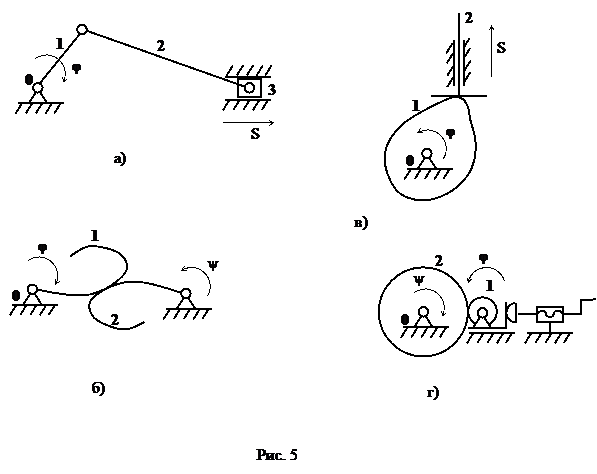
· Механизм, в котором все кинематические пары низшие, называется рычажным (рис. 5,а).

· В зубчатом механизме движение от одного звена к другому передается посредством зубчатого зацепления (рис. 5,б).

· Кулачковый механизм содержит звено со сложным профилем, называемое кулачком (рис 5,в).

· Во фрикционном механизме движение от одного звена к другому передается за счет сил трения (рис. 5,г; звенья вспомогательного винтового механизма, предназначенного для поджатия колеса 1, не пронумерованы).

Механизмы также могут быть комбинированными: например, зубчато-рычажный или зубчато-фрикционный механизмы.

По расположению в пространстве механизмы подразделяются на плоские и пространственные.

· Механизм называется плоским, если траектории точек всех его подвижных звеньев находятся в плоскостях, параллельных неподвижной плоскости. На рис. 5 показаны структурные схемы плоских механизмов.

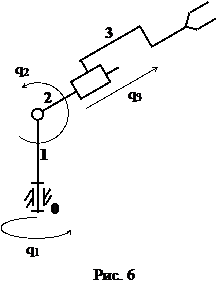
· Механизм называется пространственным, если траектории точек его подвижных звеньев лежат в непараллельных плоскостях. На рис. 6 приведена схема пространственного механизма – манипулятора, работающего в сферической системе координат.

Механизм называется замкнутым, если каждое его звено образует, как минимум, две кинематические пары. Если есть хотя бы одно звено, образующее только одну кинематическую пару, механизм – разомкнутый.

Механизм называется одноконтурным, если он содержит один замкнутый кинематический контур. Если в механизме имеется более чем один замкнутый контур, то механизм – многоконтурный. На рис. 5 приведены схемы замкнутых одноконтурных механизмов; на рис. 6 – схема разомкнутого механизма, не имеющего замкнутых кинематических контуров.

Контрольные вопросы

1. Что называется кинематической парой?

2. Что называют подвижностями кинематической пары?

3. Как определяется класс кинематической пары?

4. Может ли кинематическая пара иметь класс выше пятого? Обоснуйте свой ответ.

5. Какие кинематические пары называются низшими? Высшими?

6. Чем отличается структурная схема механизма от его кинематической схемы?

7. Перечислите разновидности механизмов по функциональному назначению.

8. Какие механизмы называются рычажными?

9. Чем отличается плоский механизм от пространственного механизма?

10. Сформулируйте условие, в соответствии с которым механизм определяется как замкнутый.

11. Может ли разомкнутый механизм иметь замкнутые кинематические контуры? Обоснуйте свой ответ.

Местные подвижности

Местными подвижностями называются степени свободы механизма, не оказывающие влияния на передачу основного движения.

Рассмотрим механизм (Рис. 9). По формуле Сомова – Малышева число его степеней свободы ( , , )

.

То есть, этот механизм не только существует как пространственный, но еще имеет две степени свободы. Одна степень свободы здесь является основной подвижностью, необходимой для передачи движения от звена 1 к звену 3. Вторая степень свободы (вращение шатуна 2 вокруг собственной оси) не влияет на передачу основного движения, поэтому является местной подвижностью.

В общем случае, механизм может иметь как основные, так и местные подвижности: его число степеней свободы определяется равенством:

,

где W_O – число основных, W_М – число местных подвижностей.

Местные подвижности часто предусматривают в механизмах с целью обеспечения более благоприятного распределения нагрузки на звенья и равномерного изнашивания контактирующих поверхностей. При необходимости, местные подвижности можно устранить, повысив класс соответствующих кинематических пар.

Контрольные вопросы

1. Перечислите наиболее часто используемые плоские четырехзвенные рычажные механизмы. Приведите примеры машин или приборов, в которых есть такие механизмы.

2. Чем отличается кривошип от коромысла? Коромысло от кулисы?

3. Что называют степенью свободы механизма?

4. Чем отличается механизм от конструкции?

5. Что означает множитель «6» в структурной формуле Сомова - Малышева?

6. Для каких механизмов используется структурная формула Чебышева?

7. Какие механизмы называют клиновыми? Какую структурную формулу следует использовать для расчета степеней свободы клинового механизма?

8. Что называют местной подвижностью?

9. С какой целью местные подвижности предусматривают в механизмах?

10. Как можно устранить местную подвижность?

Избыточные связи

Избыточными называют такие связи, которые не накладывают новых ограничений на перемещения звеньев механизма, а только повторяют уже существующие. Избыточные связи могут быть как в отдельных кинематических парах, так и на уровне механизма в целом. Различают избыточные связи трех типов: А, Б и В (по предложению профессора Озола).

Избыточные связи типа А имеют место в отдельных кинематических парах. Для передачи усилия от одного звена к другому теоретически достаточно контакта в одной точке (Рис. 10,а). Если передача усилия обеспечивается поверхностным контактом, то соприкосновение звеньев во всех точках поверхности, кроме одной, будет образовывать избыточные связи типа А (Рис. 10,б). Избыточные связи типа А являются полезными, когда требуется передача значительных усилий, поскольку звенья реальных механизмов не являются абсолютно твердыми, и в случае точечного контакта при большой силовой нагрузке будут иметь место существенные деформации, возможно также разрушение звеньев в зоне их соприкосновения.

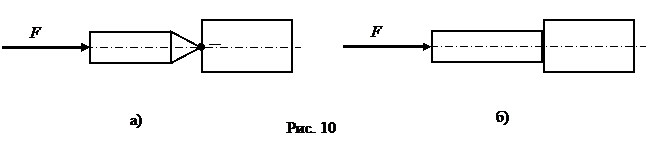В отдельных случаях связи типа А являются вредными и устраняются. Например, кинематическая пара цилиндр-поршень в двигателе внутреннего сгорания будет работоспособной, если поверхностный контакт поршня с цилиндром заменить линейным контактом цилиндра с компрессионными кольцами (Рис. 11).

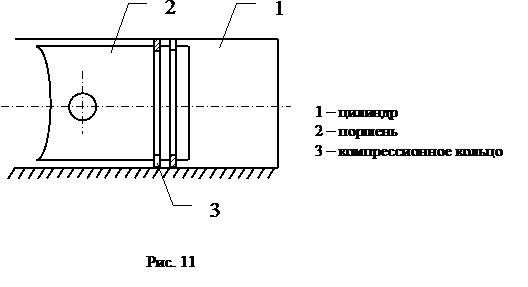Избыточные связи типа Б имеют место в кинематических парах с ветвлением. Число избыточных связей типа Б рассчитывается по формуле:

,

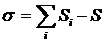где i - индекс ветвления пары, S_i – число независимых связей в i – той ветви, S – класс кинематической пары.

Пример

На рис. 12 изображена поступательная кинематическая пара с двумя ветвлениями.

Рассчитаем число избыточных связей типа Б: , (ветвление поступательное), (ветвление цилиндр-плоскость) 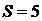(класс поступательной пары – пятый),

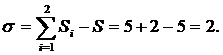
Избыточные связи типа Б увеличивают жесткость кинематической пары, но требуют повышенной точности изготовления звеньев и сборки пары.

Избыточные связи типа В образуются при замыкании кинематических цепей в контуры, отсюда их второе название – контурные избыточные связи. Их число определяется по формуле Озола:

,

где W – число степеней свободы механизма, k – число замкнутых кинематических контуров, f – суммарное число степеней свободы кинематических пар механизма. Для плоского механизма число контурных избыточных связей может быть также найдено по формуле Малышева:

,

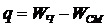где W_Ч – число степеней свободы механизма, рассчитанное по формуле Чебышева, W_СМ – число степеней свободы того же механизма, рассчитанное по формуле Сомова – Малышева.

Задача

Определить число избыточных связей в плоском шарнирном четырехзвенном механизме (Рис. 7,а).

Решение

Для данного механизма 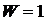, 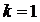(один замкнутый контур) и 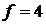(четыре одноподвижные кинематические пары). Тогда по формуле Озола:

.

Механизм имеет три контурные избыточные связи, что и было отмечено в Задаче 2 п. 1.6.

Контурные избыточные связи увеличивают жесткость механизма, но требуют повышенной точности изготовления звеньев и сборки механизма. При необходимости, они могут быть устранены путем понижения класса одной или нескольких кинематических пар.

Избыточные связи могут быть также привнесены в механизм путем введения в его схему дополнительных звеньев. Рассмотрим механизм сдвоенного параллелограмма (рис. 13).

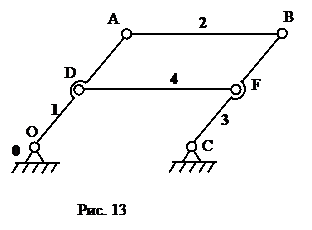Здесь дополнительное звено – шатун 4. Так как механизм плоский, рассчитаем его число степеней свободы по формуле Чебышева ( , ):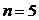

.

Полученный результат означает, что с точки зрения структурного строения, рассматриваемая система механизмом не является. Для того чтобы возникла одна степень свободы, требуется соблюдение геометрических условий: 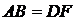, , , 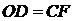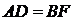. Следовательно, введение дополнительных звеньев в схему механизма влечет за собой необходимость точного соблюдения определенных геометрических размеров при изготовлении звеньев.

Силовой анализ механизма

Дадим постановку задачи силового анализа. Известны: кинематическая схема механизма, результаты его структурного и кинематического анализа, массово-геометрические характеристики звеньев (массы, центры масс, моменты инерции относительно осей, проходящих через центры масс), характеристики рабочих процессов. Известны также активные силы, приложенные к звеньям (ветровая нагрузка, силы тяжести, силы упругости пружин и т.п.). Требуется определить:

· главные векторы и главные моменты сил реакций в кинематических парах механизма;

· Обобщенные движущие силы и моменты на входных звеньях механизма.

В приближенных расчетах на ранних стадиях проектирования силовой анализ механизма проводят в предположении, что звенья – абсолютно твердые тела. Ясно, что силовой анализ требует предварительной конструкторской проработки механизма, так как приближенные значения массово-геометрических характеристик звеньев могут быть получены, если известны основные геометрические размеры звеньев и материалы, из которых они будут изготовлены.

Результаты силового анализа в дальнейшем проектировании механизма используются следующим образом. Информация о силах и моментах реакции в кинематических парах позволяет, при необходимости, рассчитать силы трения и уточнить силовой расчет механизма, а также выполнить прочностные расчеты звеньев. Информация о движущих силах и моментах дает возможность рассчитать энергетические характеристики машины и правильно спроектировать привод. Кроме того, имея результаты силового анализа, можно решать оптимизационные задачи проектирования (например, спроектировать механизм, обладающий наименьшей массой или наибольшим коэффициентом полезного действия). Таким образом, силовой анализ является важным этапом исследования механизмов в решении задач проектирования и модернизации машин.

Уравнения кинетостатики

Слово «кинетостатика» образовано сочетанием двух греческих слов: kinetos – движение, statos – покой, равновесие. То есть, «кинетостатика» означает «равновесие в движении» или «динамическое равновесие». Уравнения кинетостатики звена механизма, как твердого тела, в векторной форме имеют вид:

, ,

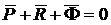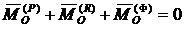Здесь 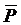, 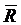- главные векторы активных сил и сил реакций, приложенных к звену, 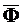- главный вектор сил инерции звена; 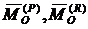- главные моменты активных сил и сил реакций относительно некоторого центра O, 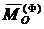- главный вектор сил инерции звена относительно того же центра O. Главный вектор и главный момент сил инерции звена вычисляются по формулам:

, ,

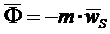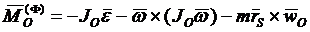где 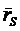- радиус-вектор, 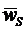- ускорение центра масс, 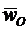- ускорение центра O, m – масса звена; 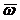- угловая скорость, 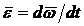- угловое ускорение звена, J_O – тензор инерции звена относительно центра O. Таким образом, в каждый момент времени, действующие на звено силы уравновешиваются силами инерции звена, а моменты сил, приложенные к звену, уравновешиваются моментами сил инерции звена. Это утверждение представляет собой известный из теоретической механики принцип Даламбера, сформулированный по отношению к твердому телу.

В случае плоского механизма, вектор главного момента сил инерции звена относительно центра масс S будет определяться своими декартовыми координатами:

, , .

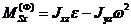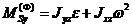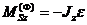В проекциях на оси декартовой системы координат векторные уравнения кинетостатики звена равносильны шести скалярным уравнениям:

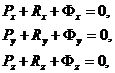
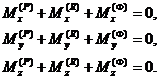
Если механизм плоский и Oxy – плоскость движения звеньев, то три из приведенной системы уравнений становятся тождественно равными нулю и остаются лишь три скалярных уравнения кинетостатики для каждого звена:

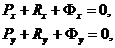
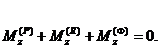
Таким образом, для пространственного механизма требуется составить и решить 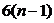, а для плоского - 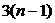скалярных уравнений кинетостатики, где n – число звеньев механизма. Эти системы уравнений могут быть решены аналитически, а в случае плоского механизма векторные уравнения сил удобно решать с помощью метода векторных планов. Для каждого нового положения механизма систему уравнений кинетостатики необходимо составлять и решать заново. Поэтому силовой расчет механизма является довольно трудоемкой задачей, решение которой целесообразно автоматизировать с помощью компьютера.

Теорема Жуковского

Как известно, динамика одноподвижного механизма с идеальными связями подчиняется принципу Даламбера, который может быть сформулирован в следующем виде:

,

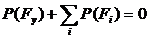где 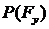- мгновенная мощность уравновешивающей силы, 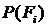- мгновенные мощности активных сил, действующих на механизм, включая силы инерции. В качестве уравновешивающей силы выступает сила, развиваемая приводом механизма.

В случаях, когда ставится задача вычисления только обобщенных движущих сил, проводить трудоемкий расчет по уравнениям кинетостатики нецелесообразно. Если имеются векторные планы скоростей, то определить движущую силу или момент можно методом Жуковского, который основан на принципе Даламбера и теореме Жуковского:

· Мгновенная мощность силы, приложенной к звену, пропорциональна моменту этой же силы относительно полюса повернутого на 90⁰ плана скоростей механизма.

Для доказательства теоремы рассмотрим звено механизма (Рис. 28,а).

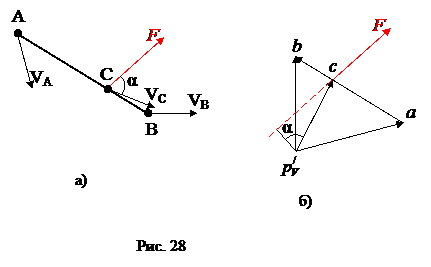Мгновенная мощность силы F определяется равенством:

,

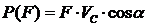где V_C – абсолютная скорость точки С, в которой действует сила.

Момент силы F относительно полюса повернутого на 90⁰ плана скоростей, как видно из рис. 28б, вычисляется по формуле:

.

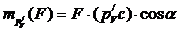Так как 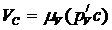, где 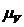- масштаб плана скоростей, то окончательно имеем:

,

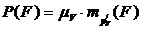что и требовалось доказать.

СТРУКТУРНЫЙ АНАЛИЗ

Рассмотрим исполнительный механизм строгального станка, изображенный на рис. 30. Данный механизм состоит из шести звеньев: стойка 0, кривошип 1, ползушки 2 и 4, кулиса 3, суппорт 5 с установленным на нем резцом. Звенья механизма образуют семь кинематических пар: 0 – 1, 1 – 2, 0 – 3, 3 – 4 – вращательные, одноподвижные, пятого класса; 2 – 3, 4 – 5 – поступательные, одноподвижные, пятого класса; 5 – 0 – цилиндрическая, двухподвижная, четвертого класса. Указанные кинематические пары – низшие; следовательно, рассматриваемый механизм является рычажным. Звенья механизма движутся в плоскостях, параллельных неподвижной плоскости – исследуемый механизм является плоским. Он не содержит звеньев, образующих только одну кинематическую пару; следовательно, является замкнутым. Звенья механизма образуют два замкнутых контура: 0 –1 – 2 –3 – 0 и 0 – 3 – 4 – 5 – 0. Число степеней свободы механизма определим, применяя универсальную формулу Чебышева

,

где n – число звеньев, p_Н – число низших кинематических пар. В рассматриваемом механизме n = 6, p_Н = 7, поэтому - механизм обладает одной степенью свободы. Выявим избыточные связи: кинематическая пара стойка-суппорт, как видно на структурной схеме, имеет ветвление: число избыточных связей типа Б определим по формуле

,

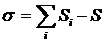где i - индекс ветвления пары, S_i – число независимых связей в i – той ветви, S – класс кинематической пары. Так как в данном случае , (оба ветвления цилиндрические) и (класс цилиндрической пары – четвертый), то

Число избыточных связей, образованных при замыкании контуров (тип В), определим из формулы Малышева

,

где W_Ч – число степеней свободы, найденное по формуле Чебышева, W_СМ – число степеней свободы, найденное по формуле Сомова – Малышева: , i – класс кинематических пар, p_i – число кинематических пар класса . В данном случае и . Таким образом, в механизме имеется четыре избыточные связи типа Б и пять избыточных связей типа В.

В соответствии с принципом Ассура, выделим начальный механизм, обладающий числом степеней свободы всего исследуемого механизма. Этот механизм – кривошипный, состоит из стойки 0 и кривошипа 1 (рис. 31). Остальные звенья образуют ведомую цепь, имеющую нулевую подвижность относительно звеньев начального механизма. Ведомая цепь, в свою очередь, состоит из двух двухзвенных структурных групп: 2 – 3 и 4 – 5.

На рис. 2 штриховой линией обозначены внешние кинематические пары – «поводки», которыми звенья групп присоединяются к начальному механизму или к звеньям соседних групп.

КИНЕМАТИЧЕСКИЙ АНАЛИЗ

СИЛОВОЙ АНАЛИЗ

5.1.Определение неизвестных сил методом векторных планов

Найдем силы реакций в кинематических парах и движущий момент, приложенный к кривошипу 1, для положения механизма, изображенного на рис. 39. Значение силы резания P и параметры звеньев даны в таблице 3.

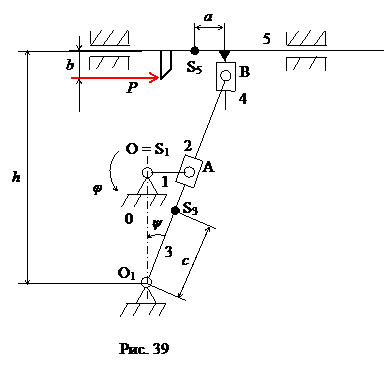Таблица 3

P, кН	h, м	a, м	b, м	c, м	m1, кг	m3, кг	m5, кг	J3, кг∙м2
1.2	0.70	0.10	0.10	0.25	5	10	12	0.3

На кинематической схеме буквой S с указанием номера звена обозначены центры масс соответствующих звеньев. Массами ползушек 2 и 4, а также силами трения в кинематических парах пренебрегаем.

Рассмотрим выходную группу звеньев 5-4. Выделим суппорт 5, обозначая все действующие на него силы (рис. 40).

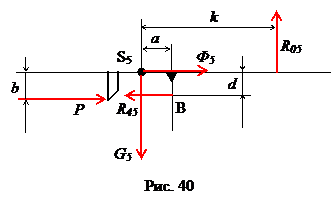Сила инерции суппорта Ф₅ приложена в его центре масс и направлена в сторону, противоположную ускорению w_B5 (см. план ускорений на рис. 38). Равнодействующая сил тяжести суппорта G₅ также приложена в центре масс и направлена вертикально вниз. Сила реакции R₄₅ со стороны ползушки 4 приложена в точке B, так как ползушки имеют малые линейные размеры, и направлена под прямым углом к поверхности, вдоль которой перемещается ползушка 4. Равнодействующая R₀₅ сил реакции стойки направлена под прямым углом к поверхности, вдоль которой перемещается суппорт, но плечо k этой силы относительно центра масс суппорта неизвестно. Проанализировав характер нагрузки на суппорт 5, заключаем, что необходимо определить три неизвестные величины: модули сил реакций R₄₅, R₀₅ и расстояние k. Для этого нам необходимо составить и решить три независимых уравнения кинетостатики звена. Уравнение сил в горизонтальном направлении имеет вид (силы, направленные вправо, учитываются со знаком «+»):

,

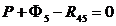откуда 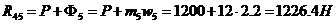. Уравнение сил в вертикальном направлении (силы, направленные вверх, учитываются со знаком «+»):

,

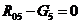откуда 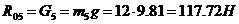. Уравнение моментов относительно центра масс S₅ суппорта (моменты сил, действующие против часовой стрелки, учитываются со знаком «+»):

,

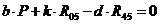откуда 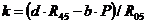. Плечо d, согласно рис. 11, найдем из соотношения

.

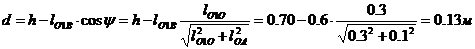Соответственно, .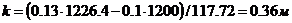

Теперь перейдем к группе звеньев 2-3. Выделим кулису 3, обозначая все действующие на нее силы (рис. 41).

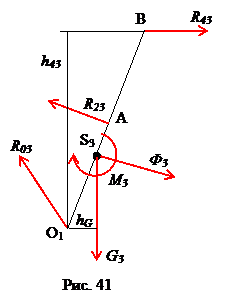
Сила тяжести кулисы 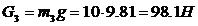, направлена вертикально вниз. Сила инерции 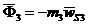, где 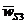- ускорение центра масс S₃ кулисы. Согласно плану ускорений (рис. 38), отрезок 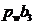, изображающий полное ускорение точки B кулисы, равен 58 мм. Значение ускорения этой точки определится как произведение длины изображающего отрезка на масштаб плана ускорений: 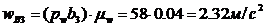. Тогда ускорение центра масс S₃ найдем из пропорции

.

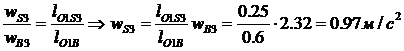Абсолютная величина силы инерции кулисы 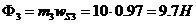, направление – в сторону, противоположную ускорению центра масс. Момент сил инерции собственного вращения кулисы по абсолютной величин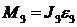е , где 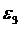- угловое ускорение кулисы, которое найдем по формуле

.

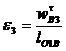Из плана ускорений имеем 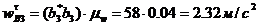, 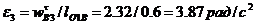. Тогда 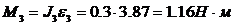, направление момента сил инерции кулисы – в сторону, противоположную угловому ускорению (рис. 13). Сила реакции R₄₃ со стороны ползушки 4 равна по модулю реакции R₄₅ и направлена в противоположную сторону. Реакция R₂₃ со стороны ползушки 2 направлена перпендикулярно перемещению ползушки 2, но неизвестен ее модуль. Реакция R₀₃ со стороны стойки неизвестна ни по модулю, ни по направлению (на рис. 41 направление этой реакции указано произвольно).

Величину реакции R₂₃ определим из уравнения моментов относительно точки O₁:

,

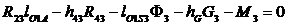откуда 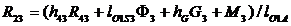. Плечо силы R₄₃ 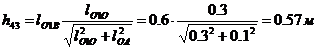, плечо силы тяжести 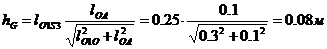. Следовательно, .

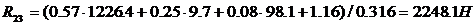Реакцию R₀₃ определим путем построения плана сил. Векторное уравнение сил имеет вид

.

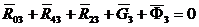Пусть реакция R₄₃ отображается на плане отрезком длины 50 мм. Тогда масштаб плана сил 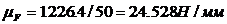. Отрезок, изображающий реакцию R₂₃: 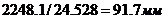; отрезки, изображающие силы G₃ и Ф₃ равны 4 мм и 0.4 мм соответственно. Ввиду малости отрезка, изображающего силу Ф₃, пренебрежем в расчете этой силой. План сил, построенный в принят<