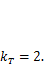Инамические нагрузки при работе механизма передвижения
При движении машины возникают горизонтальные динамические нагрузки от разгонов и торможений механизма передвижения, а также вертикальные — при проходе по неровностям пути.
Рассмотрим моделирование динамических нагрузок, возникающих при разгоне (торможении) однобалочного мостового крана с центрально расположенной тележкой, с помощью одномассовой модели (рис. 5.4, а) с параметрами т и с (п. 5.1). Основанием системы являются колеса, движущиеся по рельсу без скольжения. Масса т равна сумме приведенной массы балки и массы тележки 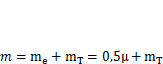 (п. 5.2). Если к тележке подвешен груз массой
(п. 5.2). Если к тележке подвешен груз массой  на коротком или жестком подвесе, то
на коротком или жестком подвесе, то 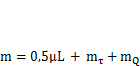 .Пренебрегая силами сопротивления, будем считать, что в процессе разгона на массу действует горизонтальная сила F= am,гдеа = V/T— среднее ускорение при разгоне. Сила мгновенно возникает (т. е. за время, существенно меньшее, чем период собственных колебаний моста) и действует в течение времениТ, после этого она исчезает и мост движется с постоянной скоростью, совершая свободные колебания. Таким образом (рис. 5.4, б),
.Пренебрегая силами сопротивления, будем считать, что в процессе разгона на массу действует горизонтальная сила F= am,гдеа = V/T— среднее ускорение при разгоне. Сила мгновенно возникает (т. е. за время, существенно меньшее, чем период собственных колебаний моста) и действует в течение времениТ, после этого она исчезает и мост движется с постоянной скоростью, совершая свободные колебания. Таким образом (рис. 5.4, б),
При 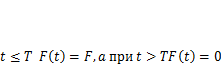 (5.7)
(5.7)
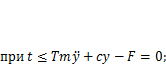 (5.8)
(5.8)
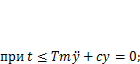 (5.9)
(5.9)
Начальные условия для решения уравнения (5.8):
при  (5.10)
(5.10)
Преобразуем уравнение (5.8) к виду
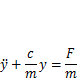
и, обозначив 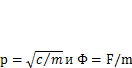 ,представим как
,представим как
 (5.11)
(5.11)
Полученное выражение является обыкновенным неоднородным дифференциальным уравнением с постоянными коэффициентами. Его решение находится как сумма 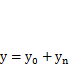 общего решения (
общего решения (  ) соответствующего однородного уравнения
) соответствующего однородного уравнения 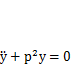 и частного решения (
и частного решения (  ) неоднородного уравнения (5.11). Общее решение однородного уравнения имеет вид (5.5)
) неоднородного уравнения (5.11). Общее решение однородного уравнения имеет вид (5.5)
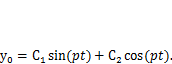
Частное решение неоднородного уравнения  ищем в форме правой части, т. е. как постоянную величину
ищем в форме правой части, т. е. как постоянную величину 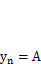 . Ее значение найдем, подставив в исходное уравнение (5.11)
. Ее значение найдем, подставив в исходное уравнение (5.11) 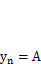 и
и  . При этом получится
. При этом получится 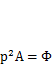 , откуда найдем
, откуда найдем 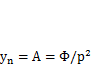 .
.
Таким образом, общее решение неоднородного уравнения (5.8) имеет вид:
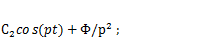 (5.12)
(5.12)
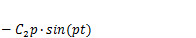 .
.
Постоянные интегрирования найдем, подставив сюда начальные условия (5.10). При этом получится 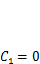 ,
, 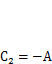 . Общее решение дифференциального уравнения (5.8) записывается как
. Общее решение дифференциального уравнения (5.8) записывается как

Максимальное перемещение, получающееся при 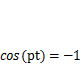 или
или 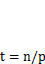 ,
, 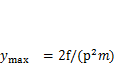 . Подставив в это выражение
. Подставив в это выражение 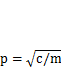 ,найдем
,найдем 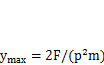 . То есть при внезапном
. То есть при внезапном
приложении нагрузки перемещение массы в два раза больше, чем при статическом нагружении силой F,при котором ys= F/с. Следовательно, мгновенное приложение силы характеризуется динамическим коэффициентом
 (5.14)
(5.14)
Если время действия силы Т <п/р =т/2, то перемещение г/maxне будет достигнуто. Рассмотрим второй этап нагружения системы (5.7) при t> Т, когда действие силы прекратилось. Уравнение движения при этом имеет вид (5.9)
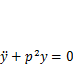
Общее решение этого уравнения в данном случае записывается как (5.5)
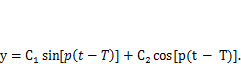 (5.15)
(5.15)
Для определения произвольных постоянных используем значения начальных условий, соответствующих окончанию первого этапа движения (5.13):
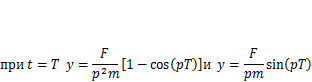
Подставив выражение (5.15) в начальные условия, найдемпроизвольные постоянные:
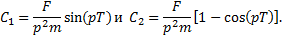
С учетом того что 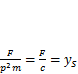 ,решение уравненияприобретет вид
,решение уравненияприобретет вид
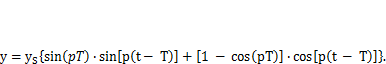
(5.16)
Примеры реализации полученных решений показаны на рис. 5.5, где приведены графики зависимости безразмерного отношения
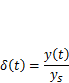
от времени tдля системы с частотой f= 1,21 Гц ( = 0,83 с) при значениях длительностиТ действия нагрузки F,равных 2 с (рис. 5.5, а) и 0,25 с (рис. 5.5, б). ПриТ = 2 с на первом этапе достигаются наибольшее отклонение массы и динамический коэффициент ψ = 2. При кратковременном силовом воздействии максимальные амплитуды колебаний и динамический коэффициент уменьшаются (ψ= 1,65), а размах колебаний возрастает (рис. 5.5, в).
С учетом результата (5.14) максимальную горизонтальную инерционнуюнагрузку на конструкцию от i-й массы
при разгоне (торможении) по второму расчетному случаю (п. 6.1) можно вычислять как
 (5.17)
(5.17)
Инерционные нагрузки первого расчетного случая 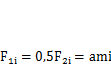 .
.
Вертикальные инерционные нагрузки, возникающие при проходе колеса через стык рельсов, учитывают с помощью коэффициента толчков kT,на который умножают веса элементов конструкции. Его максимальное значение для расчетов по второму расчетному случаю можно приближенно находить в зависимости от скорости передвижения  [10]:
[10]:

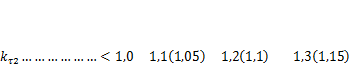
В скобках даны значения, рекомендуемые для путей с заваренными и обработанными стыками или для ходовой части, выполненной на балансирных тележках. Коэффициент толчков для расчетов по первому расчетному случаю находят как kTl= 1 + 0,5 (кт2 - 1) или К.б\ = 1 + 0,5 (kTб2 -1).
Коэффициент толчков при транспортировке по железной дороге 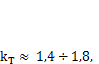 на автомобильном транспорте —
на автомобильном транспорте —