Понятие о методе конечных элементов

Метод конечных элементов (МКЭ) является в настоящее время наиболее универсальным и мощным численным ме­тодом анализа напряженно-деформированного состояния элементов конструкций, расчетов на прочность, жесткость и устойчивость. Теоретические основы МКЭ изучаются в специальном курсе и поэтому в данном учебнике не рас­сматриваются. Для реализации МКЭ имеется большой вы­бор профессиональных программ, включающих средства создания конечно-элементных моделей (препроцессор), рас­четный блок (процессор) и программу обработки и визуали­зации результатов расчета (постпроцессор) [12, 13]. Наибо­лее известными являются комплексы: ANSYS, NASTRAN, ABAQUS, COSMOSи др. Конечно-элементные процессоры встроены во многие CAD-программы (SolidWorks, MechanicalDesktopи др.). Это дает возможность проектировать конст­рукцию в ЗО-формате и оперативно проверять загруженность, прочность, жесткость и прочие параметры непосред­ственно по проектной модели (САЕ-технологии).

В МКЭ конструкция, представляющая собой некоторое сплошное тело, аппроксимируется дискретной моделью, со­стоящей из типовых элементов конечных размеров (конечных элементов — КЭ), соединенных между собой в уз­ловых точках. Этот прием позволил перейти от описания непрерывного объекта с помощью дифференциальных урав­нений к описанию свойств конечных элементов и связей между ними с помощью систем алгебраических уравне­ний. Персональные компьютеры дают возможность решать такие системы из десятков и сотен тысяч уравнений.

Для моделирования металлических конструкций обыч­но используются следующие виды конечных элементов.

1. Стержневой или балочный одномерный (ID) элемент, который имеет только один размер — длину (рис. 4.12, а). В качестве свойств этого элемента задаются характери­стики материала и геометрические параметры сечения. Эле­мент обладает 12 степенями свободы, т. е. на каждом кон­це могут быть заданы (или вычислены) шесть перемеще­ний 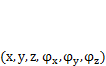, которым соответствуют шесть уси­лий (X, Y, Z, М_х, М_y, М_z). Деформирование стержневого элемента описывается с помощью теории изгиба балок без упрощения, поэтому размер элементов, использованных для моделирования стержневой конструкции, не влияет на точность расчета. В связи с этим достаточно иметь та-

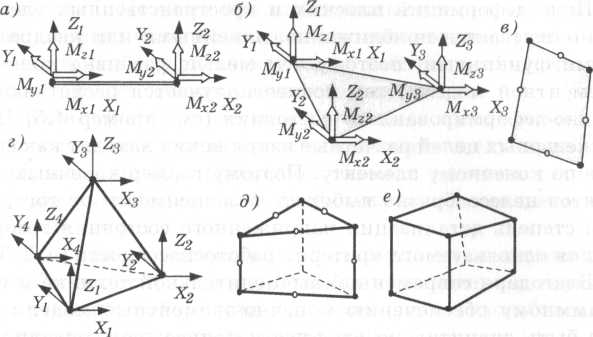Рис. 4.12. Виды конечных элементов

кие размеры элементов, чтобы узлы оказались в тех мес­тах, где изменяется сечение элемента, приложены сосре­доточенные нагрузки или необходимо задавать либо нахо­дить перемещения.

2. Плоский двумерный (2D) треугольный или четырехугольный элемент (рис. 4.12, б, в). Свойствами этого эле­мента являются характеристики материала и толщина. Элемент имеет по шесть степеней свободы в каждой вер­шине. Следовательно, в них могут быть заданы шесть пе­ремещений 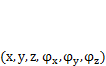или шесть усилий (X, Y, Z, М_х, Му, М_z). Для повышения точности используют эле­менты с дополнительными вершинами в середине каждой из сторон (рис. 4.12, в).

3. Пространственный трехмерный (3D) элемент, пред­ставляющий собой четырех-, пяти- или шестигранное тело (рис. 4.12, г—е). Свойствами этого элемента являются ха­рактеристики материала. Каждая вершина элемента име­ет по три степени свободы, соответствующие линейным перемещениям (х, у, z). Как и в случае 2В-элементов, для повышения точности могут быть использованы элементы с дополнительными вершинами в середине каждой из сто­рон.

Кроме того, применяют специальные конечные элементы, моделирующие контакт двух тел или зазор, пружины, канаты, мембраны и пр.

Поле деформаций плоских и пространственных элементов описывается приближенно, линейными или квадратич­ными функциями, поэтому чем мельче разбивка конечно­элементной модели, тем точнее получается расчет напря­женно-деформированного состояния (см. пример 4.5). Для инженерных целей расчетные напряжения находят как сред­ние по конечному элементу. Поэтому размер конечных эле­ментов целесообразно выбирать в зависимости от того, ка­кая степень детализации напряженного состояния требуется для используемого критерия работоспособности (п. 1.5.3).

Благодаря современной вычислительной технике и про­граммному обеспечению конечно-элементные модели мо­гут быть значительно сложнее и точнее, чем модели для аналитических расчетов. Однако следует знать, что сколь угодно сложная модель никогда не будет полностью адекватна натуре. При создании модели принимают ряд допущений, которые в той или иной степени влияют на резуль­таты расчетов. Так, например, упрощенно моделируют гео­метрию конструкции (не учитывают вспомогательные эле­менты, конфигурацию сварных швов), условия закрепления (обычно используют идеальные связи), свойства материа­ла (которые на самом деле имеют значительный разброс), характер приложения нагрузок, пренебрегают наличием дефектов и неточностей изготовления, остаточных свароч­ных напряжений и деформации и др. Таким образом, методика МКЭ, как и любая расчетная методика, является приближенной. Поэтому и при использовании МКЭ ана­лиз работоспособности конструкции выполняется в рам­ках системы расчета СРДН или СРПС (п. 1.5.2), хотя зна­чения коэффициентов надежности могут отличаться от при­нимаемых при аналитических расчетах.

4.5.2. Применение метода конечных элементов для анализа напря­женно-деформированного состояния конструкций

В инженерной практике конечно-элементное исследование является не целью, а частным инструментом прогно­зирования поведения конструкции под влиянием внешних воздействий. Поэтому при планировании и реализации ко­нечно-элементного исследования необходимо учитывать структуру и допущения критерия работоспособности, для которого будут использованы его результаты.

Планирование конечно-элементного исследования должно включать следующие дей­ствия, которые обуславливают объем и качество ожидае­мых результатов, а также необходимые временные и фи­нансовые затраты.

1. Постановка цели и условий конечно-элементного расчета. То есть определение объекта исследования, перечня исследуемых свойств или критериев работоспособности и комплекса учитываемых воздействий.

2. Предварительное определение конфигурации и разме­ров рассчитываемой конструкции. Для трансформируемых конструкций необходимо задать перечень степеней подвижности, влияние которых должно быть исследовано.

3. Определение объекта моделирования и границ модели. Она может включать конструкцию в целом, отдельный эле­мент или узел. Определение степени детализации модели, которая зависит от целей расчета. То есть решение вопросов о том, какие фрагменты конструкции должны быть смоде­лированы, а какими можно пренебречь (например, сварные швы, вспомогательные элементы, галереи, ограждения).

4. Определение условий закрепления конструкции (гра­ничных условий) и условий соединения элементов между собой. Решение вопроса о необходимости моделирования контактов, учета переменности характеристик основания и пр.

5. Составление перечня действующих нагрузок, правил их вычисления и перечня вариантов расчета с указанием расчетных нагрузок.

6. Выбор программного обеспечения. В тех случаях, ко­гда имеется единственный программный продукт, его воз­можности следует учитывать при решении вопросов, ука­занных в предыдущих пунктах.

Разработка конечно-элементной модели для расчета конструкции включает следующие операции.

1. Выбор типа и свойств элементов производится в за­висимости от характера анализируемой конструкции и целей расчета. Для получения картины распределения но­минальных напряжений и внутренних усилий в балках, рамах и элементах ферм во многих случаях достаточно использовать стержневые элементы (рис. 4.13). Плоские (2D) элементы удобны для анализа как общего, так и мест 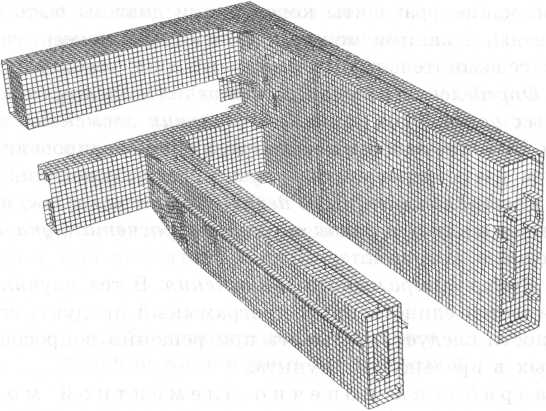Рис. 4.14. Фрагмент пространственной конечно-элементной модели конструкции специального мостового крана, по­строенной из пластинчатых элементов

ного напряженно-деформированного состояния тонкостен­ных конструкций всех видов (рис. 4.14). При необходимо­сти в одной модели могут использоваться элементы раз­ных видов, например плоские — в той зоне, где необходи­мо проанализировать локальное напряженное состояние, и стержневые — в тех областях, где достаточно знать толь­ко номинальные напряжения и общие перемещения. Про­странственные (3D) элементы целесообразно применять для анализа местного напряженно-деформированного состоя­ния сложных пространственных узлов, в которых толщины элементов сопоставимы с характерными размерами узла. В зависимости от целей расчета используют модели идеально упругого или упругопластического материала (п. 1.5.3). Густота конечно-элементной сетки также зависит от целей расчета и особенностей конструкции. В соот­ветствующих разделах даны рекомендации по выбору размеров КЭ в зависимости от расчетного критерия работо­способности (см. п. 7.2, гл. 8, п. 9.4.1, 10.1.6).

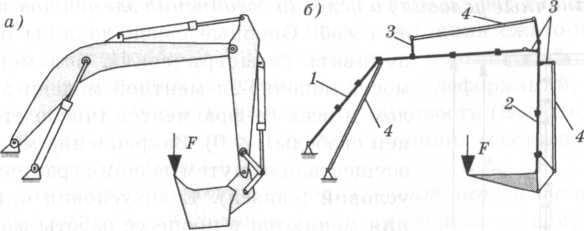Рис. 4.15. Схема стреловой системы экскаватора (а) и ее стержне­вая КЭ-модель (б):

1 и 2 — основные элементы конструкции; 3 и 4 — вспомогательные абсолютно жесткие элементы (черными квадратиками показаны узлы конечно-элементной сетки)

2. Создание геометрического образа модели. В стержневой модели оси стержневых КЭ должны совпадать с ося­ми моделируемых стержней и балок. Этим элементам при­сваиваются параметры сечений соответствующих элемен­тов конструкции (рис. 4.15, поз. 1, 2). Для приложения нагрузок, не проходящих через ось балки (стержня), ис­пользуют вспомогательные абсолютно жесткие стержни

(поз. 3). Они также могут использоваться для моделирова­ния элементов привода (например, гидроцилиндров, поз.4), фиксирующих стержневую систему в расчетном поло­жении. Абсолютно жесткие стержни можно также исполь­зовать для эксцентричного присоединения элементов, на­пример в балочно-ферменных конструкциях (рис. 4.16).

При создании модели из плоских КЭ они должны соот­ветствовать срединной плоскости элементов конструкции (рис. 4.17). При этом высота модели балки 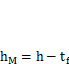(h — высота балки; t,— толщина пояса). Для пространственных конструкций и узлов следует оценить возможность использования симметрии конструкции и нагрузок.

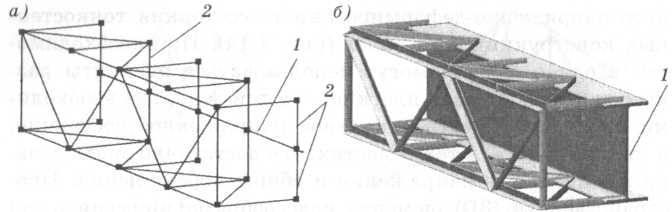Рис. 4.16. Стержневая конечно-элементная модель балочно-ферменной конструкции: а — структурная модель; б — модель с визуализацией сечений элементов; 1 — балочный элемент двутаврового сечения; 2 — вспомогательные абсолют­но жесткие элементы

3.

Моделирование условий закрепления конструкции (граничные условия) и условий соединения элементов между собой. Опорные связи должны обес­печивать геометрическую неизменяе­мость конечно-элементной модели в це­лом и всех ее фрагментов (число степе­ней свободы i< 0). Закрепление модели осуществляют путем задания граничных условий (связей). Если условия опира- ния меняются в процессе работы машины из-за переменной податливости основания, погрешности изготовления, чения двутавровой нарушения контакта и пр., то следует предусмотреть несколько вариантов закрепления конструкции, чтобы выявить наиболее небла­гоприятную ситуацию. При расчетах несущей конструкции опорная часть машины (колеса, подвеска, шарнирные опо­ры и пр.) может описываться условными элементами, не отражающими ее конструкции, но моделирующими геомет­рию и кинематику связи с опорными точками основания.

4. Моделирование условий нагружения конструкции в виде комбинации нагрузок, одновременно действующих на конструкцию в соответствии с таблицей нагрузок (гл. 6). Значения нагрузок и перечень нагрузок, входящих в комбинацию, устанавливают в зависимости от типа ма­шины и целей конечно-элементного исследования. Как правило, рассматривают несколько комбинаций нагрузок. Локальные нагрузки прикладывают к одному или несколь­ким узлам. Распределенные нагрузки (как, например, сила тяжести конструкции или ветровое давление) приклады­вают по объемам либо площадям модели.

5. Выбор вида расчета в зависимости от поставлен­ных целей. Основными видами конечно-элементных расче­тов несущих конструкций являются:

• статический расчет (Static), который используют при анализе напряженно-деформированного состояния конструкции из упругих материалов под действием внешних сил и тепловых воздействий, для проверки по условиям проч­ности и жесткости;

• нелинейный статический расчет (NonlinearStatic) вы­полняют по деформированной схеме, используют для ана­лиза напряженно-деформированного состояния сжато-изо­гнутых элементов (п. 9.2.2), конструкций повышенной гиб­кости, исследования упругопластических деформаций;

• расчет на общую и местную устойчивость (Buckling);

• динамические расчеты (Dynamic), анализ собственных частот (NormalModes) и др.

6. Анализ результатов конечно-элементного расчета — финальная часть исследования. Его методика зависит от целей анализа, т. е. исследуемого критерия работоспособ­ности конструкции. При этом необходимо иметь в виду, что основные инженерные условия работоспособности со­зданы для аналитических расчетов и простая подстановка в них результатов расчета МКЭ может привести к ошиб­кам, правда в большинстве случаев в запас надежности. Анализ этих ситуаций рассмотрен в главах, посвященных соответствующим критериям работоспособности.

Примеры применения МКЭ

Пример 4.5. Расчет концентрации напряжений в свар­ном узле. В конечно-элементных моделях тонкостенных крупногабаритных конструкций можно использовать плос­кие (2D) элементы. При этом в узлах стыковки элементов, окончания ребер, присоединения кронштейнов получают­ся острые углы без притуплений, которые в реальной кон­струкции образуют сварные швы. Уровень расчетных на­пряжений в таких узлах существенно зависит от разме­ров КЭ.

Рис. 4.18. Конечно-элементная модель узла (а) и график зависимости коэффициента концентрации от размера КЭ (б)

Рассчитаем напряженно-деформированное состояние симметричного узла конструкции с продольным ребром (рис. 4.18, а). Геометрический параметр моделиа = 80 мм. Материал модели идеально упругий. Узлы, отмеченные чер­ными квадратиками, закреплены: два узла от перемещения по указанным направлениям, остальные по оси х. Модель нагружалась растяжением с номинальными напря­жениями = 100 МПа. Конечно-элементная модель по­строена из плоских элементов, размеры которых варьировались от 20 до 1 мм. Теоретический коэффициент

концентрации напряжений вычисляется как 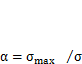, где 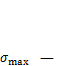максимальное напряжение, определяемое в центре наиболее нагруженного КЭ в месте окончания продоль­ного ребра. Как видно из графика (рис. 4.18, б), с уменьшением размера КЭ значение коэффициента концентрации увеличивается c 1.2 до 2.6 и при дальнейшем уменьшении элементов будет расти. Это обстоятельство необходимо учитывать при использовании полученных результатов в кри­териях работоспособности.

Пример 4.6. Нелинейный статический расчет. Выполним вычисление внутренних усилий в стреле с оттяжкой, загруженной собственным весом и сосредоточенной нагрузкой на конце (п. 9.2.2, пример 9.1).

Конечно-элементная модель построена из стержневых эле­ментов (рис. 4.19). Рассмотрим два варианта нагружения:

1) при загрузке собственным весом и силой F_z= 20 кН на конце;

2) при загрузке собственным весом и силами F_z= 20 кН иF_y = 1 кН.

Для каждого варианта нагружения выполнены статический расчет (Static) и расчет по деформированной схеме (NonlinearStatic). Получены следующие результаты (рис.

Рис. 4.19. Эпюры моментов, построенные по результатам конечно-элементных рас­четов

Нагружение 1, статический расчет:

• сила сжатия стрелы S_b= 191 кН;

• изгибающий момент в стреле при х = 0,5lL

М_у0 = 16,5 кН м;

• прогиб стрелы при х = 0,5L

.

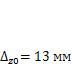Нагружение 1, нелинейный статический расчет:

• сила сжатия стрелы

S_b= 191 кН;

• изгибающий момент в стреле при х = 0,5L

M_y0= 19,3 кН-м;

• прогиб стрелы при х = 0,5L

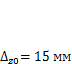
Нагружение 2, статический расчет:

• изгибающий момент в стреле при х = 0,5L

M_y0= 16,5 кН-м;

• изгибающий момент в стреле при х = 0

М_г1 = 15,0 кН-м;

• изгибающий момент в стреле при х = 0,5L

М_г0 = 7,5 кН-м.

Нагружение 2, нелинейный статический расчет:

• изгибающий момент в стреле при х = 0,51,

M_y0 = 19,3 кН• м;

• изгибающий момент в стреле при х =0

М_г1 = 15,0 кН-м;

• изгибающий момент в стреле при х - 0,5L

М_z0 = 11,0 кН • м.

Таким образом, в первом варианте нагружения стрелы изгибающий момент и прогиб при нелинейном расчете воз­росли на 15-18 %. Во втором случае изгибающий момент в корне не изменился, но в середине стрелы вырос на 47 %. Этот эффект проанализирован в примере 9.1.