Для домашней контрольной работы и методические указания по их выполнению
МИНИСТЕРСТВО ОБРАЗОВАНИЯ, науки и молодежи
РЕСПУБЛИКИ КРЫМ
Государственное бюджетное профессиональное образовательное учреждение республики Крым
СИМФЕРОПОЛЬСКИЙ КОЛЛЕДЖ
РАДИОЭЛЕКТРОНики
| Рассмотрено на заседании ЦМК № 1 Протокол № __________ «___»________ 201 __ г. Председатель ________________О.В.Гнатко | УТВЕРЖДЕНО Методсоветом ГБПОУРК СКР _____________В.И.Полякова «___»__________ 201 г. |
Задания
Для домашней контрольной работы и методические указания по их выполнению
для студентов заочной формы обучения
по дисциплине «Элементы высшей математики»
(название дисциплины)
Специальность: 09.02.01 «Компьютерные системы и комплексы»
Разработал преподаватель
_____________И.И.Фролова
(ФИО преподавателя)
«___»_______________2015 г
Симферополь, 2015 г
Практикум содержит задачи для контрольных работ по всем курсам математических дисциплин, предусмотренным учебными планами специальностей, и краткий перечень вопросов для подготовки к экзаменам.
СОДЕРЖАНИЕ
Требования к оформлению контрольных работ. 2
Формирование исходных данных к задачам. 2
1. Линейная алгебра. 3
2. Аналитическая геометрия. 3
3. Дифференциальное исчисление. 4
4. Интегральное исчисление. 4
5. Дифференциальные уравнения. 4
6. Комплексные числа. 5
Краткое содержание (программа) курса. 6
Список учебной литературы.. 8
Требования к оформлению контрольных работ
1. Контрольные работы следует выполнять в ученических тетрадях в клетку. На обложке необходимо указать: название колледжа; название и номер контрольной работы; название (номер) специальности; фамилию,имя, отчество и личный шифр студента.
2. На каждой странице надо оставить поля для оценки решения задач и методических указаний проверяющего работу.
3. Условия задач переписывать полностью необязательно, достаточно указать номер задачи по данному сборнику. В условия задач надо сначала подставить конкретные числовые значения параметров т и п, и только после этого приступать к их решению.
4. Задачи в контрольной работе нужно располагать в порядке возрастания номеров.
Формирование исходных данных к задачам
Условия задач, входящих в контрольную работу, одинаковы для всех студентов, однако числовые данные задач зависят от личного шифра студента, выполняющего работу.
Числовых данных параметров т и п определяются по двум последним цифрам номера зачетной книжки (А — предпоследняя цифра, В — последняя цифра). Значение параметра т выбирается из таблицы 1, а значение параметра п - из таблицы 2. Эти два числа т и п и нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра т)
| А | ||||||||||
| т |
Таблица 2 (выбор параметра п )
| В | ||||||||||
| п |
Например, если шифр студента 1604 — 037, то А = 3, В = 7, и из таблиц находим, что т =4, п =1. Полученные т = 4 и п = 1 подставляются в условия всех задач контрольной работы этого студента.
Линейная алгебра
Действия с матрицами.
Выполнить действия:
а) 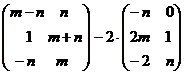 ; б)
; б) 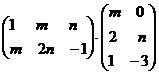 .
.
Вычисление определителей.
Вычислить определитель 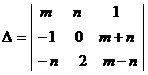 двумя способами:
двумя способами:
а) по правилу «треугольников».
Системы линейных уравнений.
Решить систему уравнений тремя способами: а) по формулам Крамера; б) с помощью вычисления обратной матрицы, записав систему в матричном виде 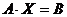 :
:
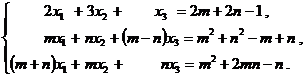
Аналитическая геометрия
Прямая на плоскости.
Построить треугольник, вершины которого находятся в точках 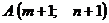 ,
, 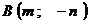 ,
, 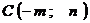 и найти:
и найти:
1) координаты точки пересечения медиан;
2) длину и уравнение высоты, опущенной из вершины А;
3) площадь треугольника;
4) систему неравенств, задающих внутренность треугольника АВС.
Дифференциальное исчисление
Производные функций.
3.1.1. Найти производные 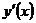 функций:
функций:
а) 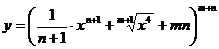 ; б)
; б) 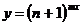 ;
;
в) 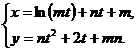
Интегральное исчисление
Неопределенный интеграл.
4.1.1. Найти интегралы:
а) 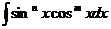 б)
б) 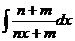
в) 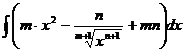 г)
г) 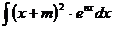 ;
;
Дифференциальные уравнения
Уравнения первого порядка.
5.1.1. Найти общее решение уравнения:
а) 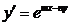 ; б)
; б) 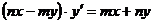 ;
;
Комплексные числа
Линейная алгебра.
Матрицы, действия над ними. Определители, их свойства и вычисление. Обратная матрица. Системы линейных уравнений, условие их совместности. Формулы Крамера, метод Гаусса и матричный способ решения систем.
Аналитическая геометрия.
Простейшие задачи аналитической геометрии (расстояние между точками, деление отрезка в заданном отношении). Прямая на плоскости, различные виды ее уравнений, угол между прямыми. Расстояние от точки до прямой.
Векторы, линейные операции над ними. Координаты вектора, его длина, направляющие косинусы. Скалярное, векторное и смешанное произведения векторов, условия их перпендикулярности, коллинеарности, компланарности.
Плоскость в пространстве, ее уравнения, угол между плоскостями, расстояние от точки до плоскости. Прямая в пространстве, ее общие и канонические уравнения. Угол между прямой и плоскостью.
Интегральное исчисление.
Неопределенный интеграл, его основные свойства. Таблица интегралов. Интегрирование подстановкой и по частям. Интегрирование дробно-рациональных, тригонометрических и иррациональных функций.
Интегральная сумма. Определенный интеграл, его геометрический смысл. Свойства определенного интеграла. Формула Ньютона-Лейбница. Интегрирование по частям и замена переменной в определенном интеграле.
Список учебной литературы
1. Бугров Я.С., Никольский С.М. Высшая математика, в трёх томах. – М: Дрофа, 2003.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2006.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Том 1,2. – М.: Высшая школа, 2000.
4. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1980.
5. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1974.
6. Пискунов Н.С. Дифференциальное и интегральное исчисления Том 1,2.— М.: Наука, 1988.
7. Письменный Д. Г. Конспект лекций по высшей математике. Части I и II. – М: «Айрис Пресс» 2004 г.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ, науки и молодежи
РЕСПУБЛИКИ КРЫМ
Государственное бюджетное профессиональное образовательное учреждение республики Крым
СИМФЕРОПОЛЬСКИЙ КОЛЛЕДЖ
РАДИОЭЛЕКТРОНики
| Рассмотрено на заседании ЦМК № 1 Протокол № __________ «___»________ 201 __ г. Председатель ________________О.В.Гнатко | УТВЕРЖДЕНО Методсоветом ГБПОУРК СКР _____________В.И.Полякова «___»__________ 201 г. |
Задания
для домашней контрольной работы и методические указания по их выполнению
для студентов заочной формы обучения
по дисциплине «Элементы высшей математики»
(название дисциплины)
Специальность: 09.02.01 «Компьютерные системы и комплексы»
Разработал преподаватель
_____________И.И.Фролова
(ФИО преподавателя)
«___»_______________2015 г
Симферополь, 2015 г
Практикум содержит задачи для контрольных работ по всем курсам математических дисциплин, предусмотренным учебными планами специальностей, и краткий перечень вопросов для подготовки к экзаменам.
СОДЕРЖАНИЕ
Требования к оформлению контрольных работ. 2
Формирование исходных данных к задачам. 2
1. Линейная алгебра. 3
2. Аналитическая геометрия. 3
3. Дифференциальное исчисление. 4
4. Интегральное исчисление. 4
5. Дифференциальные уравнения. 4
6. Комплексные числа. 5
Краткое содержание (программа) курса. 6
Список учебной литературы.. 8
Требования к оформлению контрольных работ
1. Контрольные работы следует выполнять в ученических тетрадях в клетку. На обложке необходимо указать: название колледжа; название и номер контрольной работы; название (номер) специальности; фамилию,имя, отчество и личный шифр студента.
2. На каждой странице надо оставить поля для оценки решения задач и методических указаний проверяющего работу.
3. Условия задач переписывать полностью необязательно, достаточно указать номер задачи по данному сборнику. В условия задач надо сначала подставить конкретные числовые значения параметров т и п, и только после этого приступать к их решению.
4. Задачи в контрольной работе нужно располагать в порядке возрастания номеров.
