Вопрос II. Использование знака дифференциала.

Введение.

Дифференциал (от лат. differentia «разность», «различие») – это линейная часть приращения функции.

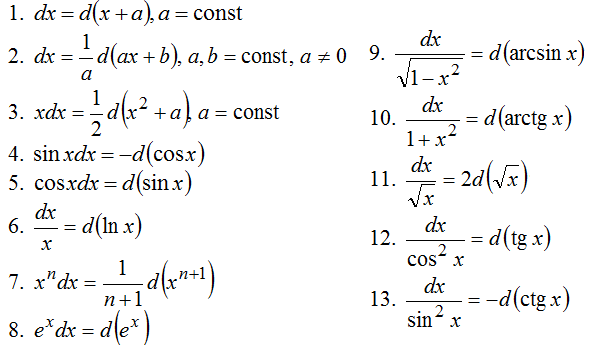
Вопрос I. Обозначения.

Обычно дифференциал функции {\displaystyle f} f обозначается {\displaystyle df} df. Некоторые авторы предпочитают обозначать {\displaystyle {\rm {d} {f} {{\rm {d} {f} шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.

Дифференциал в точке {\displaystyle x_{0}} x_{0} обозначается {\displaystyle d_{x_{0} {f} d_{{x_{0}}}f, а иногда {\displaystyle df_{x_{0}}} df_{{x_{0}}} или {\displaystyle df[x_{0}]} df[x_{0}], а также {\displaystyle df} df, если значение {\displaystyle x_{0}} x_{0} ясно из контекста.

Соответственно, значение дифференциала в точке {\displaystyle x_{0}} x_{0} от {\displaystyle h} h может обозначаться как {\displaystyle d_{x_{0}}f(h)} d_{{x_{0}}}f(h), а иногда {\displaystyle df_{x_{0}}(h)} df_{{x_{0}}}(h) или {\displaystyle df[x_{0}](h)} df[x_{0}](h), а также {\displaystyle df(h)} df(h), если значение {\displaystyle x_{0}} x_{0} ясно из контекста.

Вопрос II. Использование знака дифференциала.

1. Знак дифференциала используется в выражении для интеграла {\displaystyle \int f(x)\,dx} \int f(x)\, dx. При этом иногда (и не вполне корректно) дифференциал {\displaystyle dx} dx вводится как часть определения интеграла.

2. Также знак дифференциала используется в обозначении Лейбница для производной {\displaystyle f'(x_{0})={\frac {df}{dx}}(x_{0})} f'(x_{0})={\frac {df}{dx}}(x_{0}). Это обозначение мотивировано тем, что для дифференциалов функции {\displaystyle f} f и тождественной функции {\displaystyle x} x верно соотношение

{\displaystyle d_{x_{0}}f=f'(x_{0}){\cdot }d_{x_{0}}x.} d_{{x_{0}}}f=f'(x_{0}){\cdot }d_{{x_{0}}}x.

Вопрос III. Определения.

Для функций.

Дифференциал может быть определён напрямую, то есть, без привлечения определения производной, как функция {\displaystyle d_{x_{0}}f(h)} d_{{x_{0}}}f(h), линейно зависящая от {\displaystyle h} h, и для которой верно следующее соотношение

Вопрос V. Свойства.

Матрица линейного оператора {\displaystyle d_{x_{0}}f} d_{{x_{0}}}f равна матрице Якоби; её элементами являются частные производные {\displaystyle f} f.

Отметим, что матрица Якоби может быть определена в точке, где дифференциал не определён.

Вопрос VI. История.

Термин «дифференциал» введён Лейбницем. Изначально {\displaystyle dx} dx применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю.

Подобный взгляд оказался неудобным в большинстве разделов математики за исключением нестандартного анализа.

Вопрос VII. Вариации и обобщения.

Понятие дифференциала содержит в себе больше, чем просто дифференциал функции или отображения.

Его можно обобщать получая различные важные объекты в функциональном анализе, дифференциальной геометрии, теории меры, нестандартном анализе, алгебраической геометрии и так далее.

Отсюда получаем, что

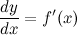
Итак, это означает, что производная может быть представлена как обыкновенная дробь – это отношение дифференциалов функции и аргумента.

Введение.

Дифференциал (от лат. differentia «разность», «различие») – это линейная часть приращения функции.

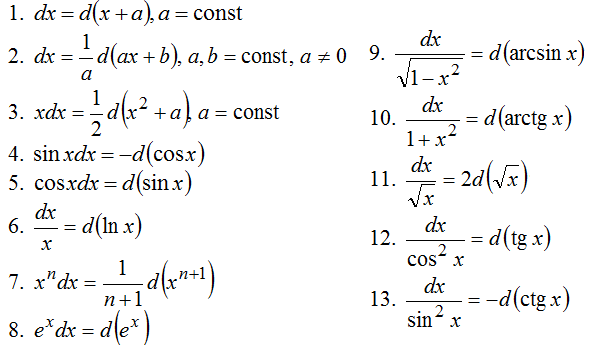
Вопрос I. Обозначения.

Обычно дифференциал функции {\displaystyle f} f обозначается {\displaystyle df} df. Некоторые авторы предпочитают обозначать {\displaystyle {\rm {d} {f} {{\rm {d} {f} шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.

Дифференциал в точке {\displaystyle x_{0}} x_{0} обозначается {\displaystyle d_{x_{0} {f} d_{{x_{0}}}f, а иногда {\displaystyle df_{x_{0}}} df_{{x_{0}}} или {\displaystyle df[x_{0}]} df[x_{0}], а также {\displaystyle df} df, если значение {\displaystyle x_{0}} x_{0} ясно из контекста.

Соответственно, значение дифференциала в точке {\displaystyle x_{0}} x_{0} от {\displaystyle h} h может обозначаться как {\displaystyle d_{x_{0}}f(h)} d_{{x_{0}}}f(h), а иногда {\displaystyle df_{x_{0}}(h)} df_{{x_{0}}}(h) или {\displaystyle df[x_{0}](h)} df[x_{0}](h), а также {\displaystyle df(h)} df(h), если значение {\displaystyle x_{0}} x_{0} ясно из контекста.

Вопрос II. Использование знака дифференциала.

1. Знак дифференциала используется в выражении для интеграла {\displaystyle \int f(x)\,dx} \int f(x)\, dx. При этом иногда (и не вполне корректно) дифференциал {\displaystyle dx} dx вводится как часть определения интеграла.

2. Также знак дифференциала используется в обозначении Лейбница для производной {\displaystyle f'(x_{0})={\frac {df}{dx}}(x_{0})} f'(x_{0})={\frac {df}{dx}}(x_{0}). Это обозначение мотивировано тем, что для дифференциалов функции {\displaystyle f} f и тождественной функции {\displaystyle x} x верно соотношение

{\displaystyle d_{x_{0}}f=f'(x_{0}){\cdot }d_{x_{0}}x.} d_{{x_{0}}}f=f'(x_{0}){\cdot }d_{{x_{0}}}x.

Вопрос III. Определения.

Для функций.

Дифференциал может быть определён напрямую, то есть, без привлечения определения производной, как функция {\displaystyle d_{x_{0}}f(h)} d_{{x_{0}}}f(h), линейно зависящая от {\displaystyle h} h, и для которой верно следующее соотношение

Вопрос V. Свойства.

Матрица линейного оператора {\displaystyle d_{x_{0}}f} d_{{x_{0}}}f равна матрице Якоби; её элементами являются частные производные {\displaystyle f} f.

Отметим, что матрица Якоби может быть определена в точке, где дифференциал не определён.

Вопрос VI. История.

Термин «дифференциал» введён Лейбницем. Изначально {\displaystyle dx} dx применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю.

Подобный взгляд оказался неудобным в большинстве разделов математики за исключением нестандартного анализа.