Связи и их реакции. Принцип освобождаемости от связей. Основные виды связей.

Аксиомы статики

А1(1 з-н Ньютона) Аксиома инерции:

Тело сохраняет первоначальное состояние покоя или равномерного прямолинейного движения до тех пор, пока другие тела не выведут его из этого состояния.

А2 (3 з-н Ньютона) Аксиома взаимодействия:

Силы взаимодействия 2 тел равны по величине и направлены по одной прямой в противоположные стороны.

А3 Условия равновесия двух сил:

Для равновесия тела, находящегося под действием 2 сил, необходимо и достаточно, чтобы эти силы были равны по величине и направлены по одной прямой в противоположные стороны.

А4 Аксиома присоединения:

Система уравновешенных сил механического состояния твердого тела не изменит, если к нему присоединить или удалить систему уравновешенных сил.

А5 Аксиома параллелограмма:

Равнодействующая двух сил, приложенных к телу в одной точке, равна по модулю и совпадает по направлению с диагональю параллелограмма, построенного на этих силах и приложенных в этой же точке.

А6 Аксиома затвердевания:

Любое тело не изменит свое механическое состояние при переходе в абсолютно твердое.

Условия равновесия системы сходящихся сил в геометрической и аналитической формах. Теорема о трех непараллельных силах.

Геометрическое условие равновесия:

Силовой многоугольник должен быть замкнут, т.е. конец последнего вектора должен совпадать с началом первого.

Аналитическое условие равновесия:

Равенство 0 проекций равнодействующей на оси координат (Rx=0, Ry=0, Rz=0).

Для равновесия тел, находящихся под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая была равна 0 (R=0).

Для равновесия тела, находящегося в системе сходящихся сил, необходимо и достаточно, чтобы были равны 0 алгебраические суммы проекций всех сил на оси произвольно выбранных систем координат.

Теорема о трех непараллельных силах:

Используется когда известны величина и направление одной силы, линия действия другой и точка приложения третьей.

Линии действия трех непараллельных уравновешенных сил, лежащих в одной плоскости, пересекаются в одной точке.

R12=F1+F2

Равновесие равнодействующей R12 сил F1 и F2 возможно только в том случае, если третья сила F3 будет направлена по линии действия R12 противоположно ей, т.е. проходить через точку пересечения линии действия сил F1 и F2.

Сложение двух параллельных сил. Момент силы относительно центра. Выражение векторного момента силы в виде векторного произведения. Аналитическое выражение момента силы относительно точки. Теорема Вариньона о моменте равнодействующей системы сходящихся сил.

Алгебраическим моментом силы F относительно некоторого центра называется взятое со знаком + или - произведение модуля силы F на плечо (кротчайшее расстояние от точки до линии действия силы). Момент положителен, если сила стремиться вращать плоскость действия против часовой стрелки и наоборот. (M=F*h) Но при этом h можно выразить через радиус-вектор r (h=r*sin α), тогда M = F*r*sin α = (Fxr). Получаем, что векторный момент силы относительно точки – векторная величина.

Т-ма Вариньона:

Момент равнодействующей пространственной системы сходящихся сил относительно какого-либо центра равен векторной сумме моментов составляющих сил относительно того же центра.

Связь между моментом силы относительно оси и векторным моментом силы относительно точки.

Mz(F)=Mo(F)*cosα Момент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось.

Сложение параллельных сил.

Равнодействующая двух параллельных сил, направленных в одну сторону равна алгебраической сумме модулей составляющих сил. Линия действия равнодействующей делит отрезок, заключённый между точками приложения сил внутренним образом на части, обратно пропорциональные модулям этих сил. Две параллельные, противоположно направленные силы, не равные по модулю, эквиваленты равнодействующей, модуль которой равен разности модулей слагаемых сил и направлены в сторону большей силы. Линия действия равнодействующей делит отрезок, заключённый между точками приложения сил внутренним образом на части, обратно пропорциональные модулям этих сил. Если модули противоположно направленных сил равны, то такая система не имеет равнодействующей, она сообщает свободному телу вращательное движение и называется парой сил.

Трение гибких тел

Для того чтобы тело находилось в равновесии, необходимо чтобы сила Р находилась в интервале Pmin˂=P˂=Pmax, а именно Q*e^(-fφ) ˂=P˂= Q*e^(fφ1)

Трение качения

При решении задач обычно силы нормальной реакции прикладывают посередине площадки по которой происходит смятие, а трение качения учитывает пары сил с моментом трения, направленным противоположно возможному движению.

Кинематика

1) Кинематика – раздел теоретической механики изучающий законы механического движения материальных точек или тел без учёта причин, вызывающих это движение. Механическое движение – изменение положения тела в пространстве с течением времени. Любое движение точки или тела рассматривается относительно какой-либо системы отсчёта. Обычно систему отсчёта связывают с землёй, считая её неподвижной. Если рассматривать движение тела относительно подвижной системы отсчёта, то при расчётах необходимо учитывать движение подвижной системы отсчёта относительно неподвижной. Траектория точки – геометрическое место последовательных положений точки в процессе её движения. Прямолинейное, если траектория-прямая, в других случаях криволинейное.

Основные задачи кинематики: - определение закона движения точки или тела в выбранной системе отсчёта. - По заданному закону определить кинематические характеристики движения.

2)Движение точки считается заданным, если существует зависимость, позволяющая определить положение точки в пространстве в произвольный момент времени, эта зависимость называется законом движения. Способы задания движения: (1) Естественный – используется. Если известна траектория движения, уравнение движения точки по этой траектории, начало отсчёта и положительное направлении движения. S=S(t) – угловая координата. (2) Векторный – положение описывается радиус-вектором проведённым из некоторой неподвижной точки. r=r(t) уравнение движения при векторном способе. Траектори в данном случае является гадографом радиус-вектора. (3) координатный – положение точки задаётся зависящими от времени дифференцируемыми функциями координат. X=x(t) y=y(t) z=z(t). y=f(x) – уравнение траектории.

3) Величина равная отношению приращения дэльта(r) вектора r к промежуточному времени дэльта(t) за который произошло это приращение называется средней скоростью точки за это время Vср.= дэльта(r)/дэльта(t). При дэльта(t) стремящимся к 0: V= dr/dt скорость точки в данный момент времени. Скорость всегда направлена по касательной к траектории движения.

4)Величина равная отношению приращения дэльта(V) вектора r к промежуточному времени дэльта(t) за который произошло это приращение называется средним ускорением точки за это время acр.= дэльта(V)/дэльта(t). При дэльта(t) стремящимся к 0: a= dV/dt ускорение точки в данный момент времени. Ускорение всегда направлена по касательной к гадографу вектора скорости.

5)V= dr/dt = d(xi+yj+zk)/dt = Vxi + Vyj + Vzk где Vx=dx/dt, Vy=dy/dt, Vz=dz/dt – проекции вектора скорости на оси координат V=корень(Vx^2+Vy^2+Vz^2)Положени вектора Vопределяется направлением косинусов , а именно углов между направлением вектора V и положительно направленной соответствующей оси координат.

6)V= dS/dt*dr/dS сдесь dS/dt – v – алгебраическая скорость точки, а dr/ds – ŧ(тау) – вектор, направленный по направлению вектора dr. V= ŧ(тау)*v.

7) Если выбрать в качестве осей координат независимые оси ŧ(тау), n, в - которые связаны с движущейся точкой при этом ŧ(тау)-является касательной, n – нормалью , в – бинормалью, тогда ŧ(тау) и n образуют касательную плоскость, n и в нормальную плоскость, в и ŧ(тау) – спрямляющуюся плоскость, это и есть естественный трёхгранник. Нормальное ускорение точки всегда направлено к центру кривизны траектории(a норм. =V^2/q, где q – радиус кривизны траектории), а касательное по касательной к траектории, если знаки касательного ускорения и скорости совпадают, то и направления их тоже совпадают, или наоборот(а ŧ(тау)=dV/dt)

8) Касательное ускорение показывает изменение скорости по величине, нормально – по направлению. Если (а ŧ(тау)=0) и ( a норм.=0) – движение равномерное и прямолинейное, если (а ŧ(тау)=0) и ( a норм. не равно 0) то криволинейное и равномерное, если (а ŧ(тау)не равно 0) и ( a норм.=0) то прямолинейное равномерное, если (а ŧ(тау) не равно 0) и ( a норм. не равно 0) то криволинейное неравномерное. При постоянном а ŧ(тау) движение либо равноускоренное, либо равнозамедленное.

9 Поступательнымназывается такое движение, при котором в теле можно выделить прямую, остающуюся параллельной самой себе в процессе движения. Т-ма: Все точки тела, движущиеся поступательно имеют в данный момент геометрически равные скорости и ускорения и движутся по одинаковым траекториям. Для изучения тела, движущегося поступательно достаточно изучить движение одной его точки, обычно рассматривают центр тяжести.

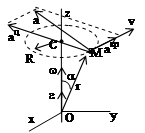10 Вращательное движение тела – такое движение твердого тела, при котором точки, принадлежащие некоторой прямой, остаются неподвижными, а остальные точки описывают окружности в плоскости перпендикулярно оси вращения. Уравнение (закон) вращательного движения: j=f(t) – угол поворота тела в радианах. Угловая ск-сть: 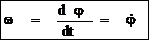, [рад/с] – определяет быстроту изменения угла поворота.

Вектор угловой скорости тела, совершающего вращение вокруг неподвижной оси, направлен вдоль оси вращения так, что если смотреть ему навстречу вращение будет против час. стрелке. Угловое ускорение тела: 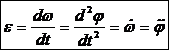, [рад/с²]. Вектор углового ускорения также направлен вдоль оси вращения. При ускоренном движении совпадает по направлению с угловой скоростью и противоположно при замедленном вращении. Угловую скорость и угловое ускорении можно представить в виде векторов, которые расположены на любой точке оси вращения.

11 Частные случаи вращения тела:

1) Равномерное вращение: w=const, j=wt, w=j/t,

2) Равнопеременное вращение: w=w₀+et; 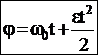, здесь начальный угол j₀=0.

Скорости и ускорения точек вращающегося тела. 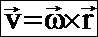– скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус–вектор этой точки. Модуль векторного произведения: v=w×r×sin(a)= w×(CM), (СМ) – расстояние от точки М до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону вращения.

12 Передаточные механизмыпредназначены для передачи вращения от ведущего вала к ведомому. Они реализуются в виде различного рода передач с жёсткой или гибкой связью. Фрекционные передачи функционируют за счёт сцепления между колёсами, зубчатые передают крутящий момент за счёт зацепления между зубьями. Отношение угловой скорости ведущего вала к угловой скорости ведомого называется передаточным числом i. Иногда хар-ка вращательного движения задаётся в виде числа оборотов в минуту.

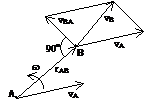
13 j,w,ε – основные кинематические характеристики вращательного движения твёрдого тела. Они одинаковы для всех точек вращательного твёрдого тела. Скорости и ускорения точек вращающегося тела. 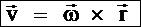– скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус–вектор этой точки. Модуль векторного произведения: v=w×r×sin(a)= w×(CM), (СМ) – расстояние от точки М до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону вращения.

a=корень((a вращ.)^2+ (a центр.)^2) = (СМ)*корень(w^4+ε^2)

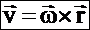
– скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус–вектор этой точки. Модуль векторного произведения: v=w×r×sin(a)= w×(CM), (СМ) – расстояние от точки М до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону вращения.

а вращ. равняется (εxr) где r это (СМ), а центр. равняется (wxV) из этого выразим а:

a=корень((a вращ.)^2+ (a центр.)^2) = (СМ)*корень(w^4+ε^2)

15 Плоскопараллельное движение твердого тела.Плоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Уравнения плоского движения: x_A= x_A (t), y_A= y_A (t), j= j (t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса. Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят.

Вопрос 16. Определение скоростей точек плоской фигуры. Теорема о проекциях скоростей точек плоской фигуры.

Теорема: Скорость любой точки принадлежащей плоской фигуре равна геометрической сумме скорости полюса и той скорости которую имела бы точка при вращательном движении вокруг оси проходящей через полюс

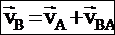
Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: v_Acosa = v_Bcosb.

Вопрос 17. Мгновенный центр скоростей. Определение скорости с помощью МЦС. Частные случаи нахождения МЦС.

МЦС – точка плоскости движения плоской фигуры, скорость которой в данном положении равна 0.

Скорости всех точек будут направлены перпендикулярно отрезкам соединяющим точку и МЦС в сторону угловой скорости и пропорциональны длинам этих отрезков.

Частные случаи определения м.ц.с.: 1) м.ц.с. – точка пересечения перпендикуляров, восстановленных к скоростям точек (напр. в точке В и точке К); 2) если скорости точек А и В параллельны между собой и перпендикулярны АВ, то для определения м.ц.с. должны быть известны модули и направления скоростей (см. v_A и v_B); 3) если они при этом равны между собой, то м.ц.с. находится в ¥, а угловая скорость w=v_A/¥=0; 4) если известно, что скорости двух точек А и В равны, параллельны и не перпендикулярны АВ, то м.ц.с. в ¥, и угловая скорость w=v_A/¥=0, если это имеет место только к некоторый момент времени, то имеем мгновенное поступательное движение; 5) если плоская фигура катится без скольжения по неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания.

Вопрос 18. Определение ускорений точек плоской фигуры. Мгновенный центр ускорений.

Ускорение любой точки плоской фигуры равно векторной сумме ускорения полюса и ускорения точки которое она имела бы при вращательном движении тела вокруг оси проходящей через полюс.

aB=aA+aBA(нормальное)+aBA(тангенциальное)=aA+aBA

aBA(нормальное)=ωAB^2*AB

aBA(тангенциальное)=έAB*AB

Существует 2 способа определения ускорений:

Метод проекций

Построение многоугольника ускорений

Мгновенный центр ускорений – точка (Q) плоской фигуры, ускорение которой в данный момент времени равно нулю. Для его построения из точки А откладываем под углом к ускорению а_А отрезок 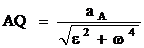, при этом угол откладывается от ускорения в сторону, направления углового ускорения e. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгн.ц. ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки и м.ц.у. один и тот же угол : 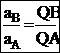. Мгновенный центр скоростей Р и мгновенный центр ускорений Q являются различными точками плоской фигуры.

Вопрос 19. Сферическое движение твёрдого тела. Углы Эйлера. Определение ускорений точек тела при сферическом движении.

Сф.движ – движение твердого тела, одна из точек которого во все время движения остается неподвижной (напр. движение волчка).

Точки тела движутся по сферическим поверхностям. Положение тела определяют при помощи трех углов. Для этого задаются две системы координат: неподвижная Оxyz и подвижная ОxhV, связанная с твердым телом. Линия ОJ – линия узлов, задаются углы: Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Таким образом уравнения сферического движения: Y=f₁(t); q=f₂(t); j=f₃(t). Углы отсчитываются от осей против хода час.стр.

Пара вращений

3) Пара вращений – вращения вокруг ||-ных осей направлены в разные стороны и угловые скорости по модулю равны ( 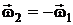– пара угловых скоростей). В этом случае v_A=v_B, результирующее движение тела – поступательное ( или мгновенное поступательное) движение со скоростью v=w₁×AB – момент пары угловых скоростей (поступательное движение педали велосипеда относит-но рамы). Мгн. центр скоростей находится в бесконечности.

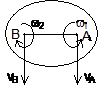
Аксиомы статики

А1(1 з-н Ньютона) Аксиома инерции:

Тело сохраняет первоначальное состояние покоя или равномерного прямолинейного движения до тех пор, пока другие тела не выведут его из этого состояния.

А2 (3 з-н Ньютона) Аксиома взаимодействия:

Силы взаимодействия 2 тел равны по величине и направлены по одной прямой в противоположные стороны.

А3 Условия равновесия двух сил:

Для равновесия тела, находящегося под действием 2 сил, необходимо и достаточно, чтобы эти силы были равны по величине и направлены по одной прямой в противоположные стороны.

А4 Аксиома присоединения:

Система уравновешенных сил механического состояния твердого тела не изменит, если к нему присоединить или удалить систему уравновешенных сил.

А5 Аксиома параллелограмма:

Равнодействующая двух сил, приложенных к телу в одной точке, равна по модулю и совпадает по направлению с диагональю параллелограмма, построенного на этих силах и приложенных в этой же точке.

А6 Аксиома затвердевания:

Любое тело не изменит свое механическое состояние при переходе в абсолютно твердое.

Связи и их реакции. Принцип освобождаемости от связей. Основные виды связей.

Тело называется свободным, если его перемещения в пространстве с течением времени ничем не ограничены.

В любом другом случае тело является несвободным.

Связи – ограничения, налагаемые на свободу любого несвободного тела.

Силы, с которыми связи действуют на данное тело, называются реакциями связей.

Принцип освобождаемости от связей:

Всякое несвободное тело можно рассматривать как свободное, если отбросить связи, заменив их реакциями.

Виды связей:

ü Гладкая поверхность (опора без трения)

ü Шероховатая поверхность

ü Цилиндрический шарнир (подшипник)

ü Сферический шарнир

ü Гибкая нить

ü Невесомый стержень

ü Жесткая заделка (защемление)

ü Опорные реакции балок

Ø Шарнирно-подвижная опора

Ø Шарнирно-неподвижная опора

Ø Жесткая заделка

4) Равнодействующая системы сходящихся сил. Геометрический и аналитический способы определения равнодействующей.

Сходящимися называются силы, линии действия которых пересекаются в одной точке.

Если у такой системы сил л.д. расположены в одной плоскости, то она называется плоской системой сходящихся сил. В любом другом случае система сходящихся сил пространственная.

Равнодействующая сходящихся сил равна геометрической сумме этих сил и приложена в точке их пересечения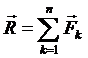

. Равнодействующая может быть найдена геометрическим способом – построением силового (векторного) многоугольника или аналитическим способом, проектируя силы на оси координат.

Геометрический способ:

Теорема: любая система сходящихся сил приводится к равнодействующей, равной геометрической сумме составляющих сил и приложенных в точках пересечения линий их действия.

Сложность данного подхода в сложности геометрических построений.

Для упрощения построений сложим геометрически силы следующим образом: конец предыдущей силы должен совпадать с началом следующего, а л.д. сил должны быть параллельны заданным.

Замыкающая, полученная таким образом, и будет являться вектором равнодействующей, причем он должен быть направлен то начала к концу.

Аналитический способ:

Проекцией силы на ось называется направленный отрезок, заключенный между перпендикулярами, проведенными к соответствующей оси из начала к концу вектора силы.

В случае пространственной системы сил используется метод двойного проецирования: сначала сила проецируется на плоскость, а затем определяются проекции полученной проекции на осях координат.