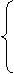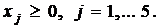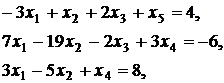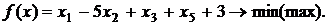Геометрическая интерпретация симплекс-метода

Рассмотренная задача ЛП в стандартной модели была решена геометрически (рис.2.5.). Многоугольник решений имеет пять вершин с координатами О (0; 0), В₃ (0; 21), Е (12; 18), С (22,5; 7,5), А₁ (25; 0). Целеваяфункция достигает максимального значения в точке Е (12; 18). В модели участвовали только две переменные х₁ и х₂.

Теперь обратимся к симплекс-таблицам и запишем опорные решения, которые там получились:

Х_опор1 = (0, 0, 300, 120, 252) (таблица 4.3.);

Х_опор2 = (0, 21, 216, 36, 0) (таблица 4.4);

Х_опор3 = Х_mах = (12, 18, 84, 0, 0) (таблица 4.5.).

Вывод: переход от одной симплекс-таблицы к другой геометрически соответствует переходу от одной вершины многоугольника к другой:

; ; .

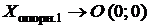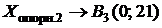Таким образом, переход осуществляется по вершинам многоугольника ОВ₃ЕСА₁, достигая своего максимального значения. На каждом шаге происходит переход к соседней вершине по ребру многоугольника. При этом целевая функция уменьшается.

Метод искусственного базиса

Постановка задачи

Для того чтобы привести задачу ЛП к канонической форме, необходимо предварительно найти некоторое начальное опорное решение этой задачи. Мы можем ввести в модель искусственные переменные, которые должны быть базисными и неотрицательными. Исключение искусственных переменных производится с помощью преобразования симплекс-таблиц. Процесс решения содержит два этапа: переход от основной модели к канонической ® решение задачи.

Пусть исходная система имеет следующий вид:

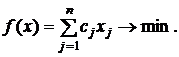
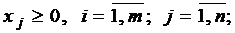
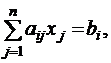
(5.1)

Без ограничения общности можно считать, что 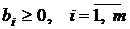. Для отыскания опорного решения строим вспомогательную задачу:

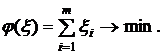
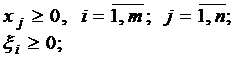
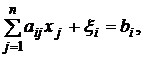
(5.2)

Свойства вспомогательной задачи:

1. Вспомогательная задача всегда имеет оптимальное решение.

2. Вектор 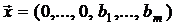является опорным решением задачи (5.2).

Таким образом, принимая этот вектор за начальное опорное решение, вспомогательную задачу можно решить симплекс-методом.

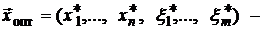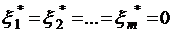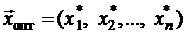Пусть оптимальное опорное решение задачи (5.2). Тогда, если , то - опорное решение исходной задачи (5.1). Если же среди чисел 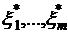есть положительные, то задача (5.1) не имеет допустимых решений. Таким образом, всегда можно либо найти опорное решение исходной задачи (5.1), либо установить ее неразрешимость.

Теоремы метода

Теорема 1. Для того, чтобы исходная система имела опорные решения, необходимо и достаточно, чтобы 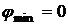(минимальное значение функции во вспомогательной задаче равно нулю).

Теорема 2. Если исходная система имеет опорные решения, то существует равносильная ей каноническая система, получаемая из завершающей таблицы вспомогательной задачи.

Замечания к теоремам

Замечание 1. Если φ_min вспомогательной задачи не равна 0, то исходная задача не обладает опорным решением (несовместна).

Замечание 2. Если при решении вспомогательной задачи:

а) в завершающей симплекс-таблице все вспомогательные переменные вышли из базиса, тогда, полагая их равными 0, получаем каноническую задачу для исходной;

б) вспомогательная переменная в некотором уравнении осталась в базисе, тогда необходимо левую часть ограничения приравнять к 0 и путем преобразований выделить базисную переменную для данного уравнения.

Следовательно, из завершающей таблицы вспомогательной задачи получим каноническую форму задачи (5.1).

Примеры решения задач

Пример 1. Пусть дана задача линейного программирования:

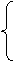5х₁ + 5х₂ – x₃ = 5,

10х₂ - х₄ = 5,

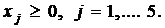х₁ + х₂ + x₅ = 5.

f(x) = 5x₂→max.

Первое и второе уравнения не имеют базисных переменных, в третьем уравнении такой переменной является х_5. Чтобы получить каноническую модель задачи, вводим две базисные переменные:

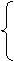5х₁ + 5х₂ – x₃ + x ₁ = 5,

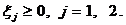10х₂ - х₄ + x ₂ = 5,

х₁ + х₂ + x₅ = 5,

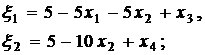
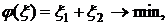где

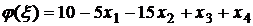, или .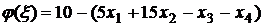

Используя систему уравнений с базисными переменными и функцию цели 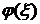, составляем исходную симплекс-таблицу.

Таблица 5.1

Базис	В	х1	х2	х3	х4	х5	ξ1	ξ2
ξ1				-1
ξ2					-1
х5
φ(x)				-1	-1

Будем вводить в базис переменную х₁ и выводить ξ₁. Преобразуем первую строку так, чтобы в клетке разрешающего элемента была единица. Для этого разделим все элементы первой строки на 5. Получим новую первую строку для следующей таблицы (табл. 5.2).

Далее необходимо получить в столбце под переменной x₁ нули. Перепишем вторую строку без изменений, так как в ней на нужном месте уже стоит нуль. Остальные нули в столбце получим, умножив получившуюся первую строку на (-1) и (-5) и сложив ее поэлементно с третьей и четвертой строкой таблицы 5.1. Получаем новую симплекс-таблицу 5.2.

Таблица 5.2

Базис	В	х1	х2	х3	х4	х5	ξ1	ξ2
х1				-1/5			1/5
ξ2					-1
х5				1/5			-1/5
φ(x)					-1		-1

Аналогично вводим в базис переменную х₂вместо ξ₂. Для этого делим вторую строку таблицы 5.2 на 10, и результат записываем во вторую строку следующей таблицы (табл.5.3). Затем умножаем получившуюся вторую разрешающую строку на (-1) и (-10) и складываем ее поэлементно с первой и четвертой строкой таблицы 5.2. Новая симплекс-таблица имеет вид:

Таблица 5.3

Базис	В	х1	х2	х3	х4	х5	ξ1	ξ2
х1	1/2			-1/5	1/10		1/5	-1/10
х2	1/2				-1/10			1/10
х5				1/5			-1/5
φ(x)							-1	-1

По теореме 1 метода искусственного базиса данная система имеет оптимальный план ( 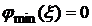), следовательно, по теореме 2 существует равносильная каноническая система, полученная из завершающей таблицы вспомогательной задачи.

Так как в завершающей симплекс-таблице вспомогательной задачи все вспомогательные переменные вышли из базиса, тогда, полагая их равными 0, получаем каноническую задачу для исходной задачи ЛП:

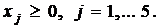
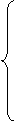
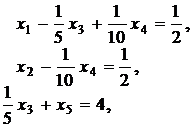
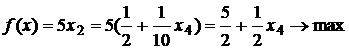или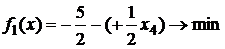

Составляем симплекс-таблицу по полученным данным:

Таблица 5.4

Базис	В	х1	х2	х3	х4	х5
х1	1/2			-1/5	1/10
х2	1/2				-1/10
х5				1/5
f1(x)	-5/2				1/2

Вводим в базис x₄. Выполняя обычные преобразования симплекс-метода и результаты вычислений запишем в табл.5.5.

Таблица 5.5

Базис	В	х1	х2	х3	х4	х5
х4				-2
х2				-1/5
х5				1/5
f1(x)	-5	-5

Вводим в базис х₃ . Получаем следующую таблицу 5.6.

Таблица 5.6

Базис	В	х1	х2	х3	х4	х5
х4
х2
х3
f(x)	-25	-5				-5

Так как в индексной строке нет положительных элементов, следовательно, получили завершающую симплекс-таблицу, в которой содержится оптимальный план задачи.

Х_опт = (0, 5, 20, 45, 0)

f_min(x) = -25 , тогда f_max(x) = 25.

Пример 2. Дана основная задача линейного программирования. При помощи элементарных преобразований матрицы коэффициентов системы ограничений, привести задачу к стандартному виду и решить ее геометрическим методом. Методом искусственного базиса получить каноническую задачу (или доказать несовместность этой системы). Решить полученную модель с помощью симплекс- таблиц (или доказать, что она не имеет оптимального плана).

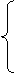
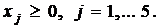
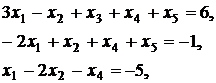
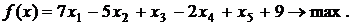
Запишем и преобразуем матрицу коэффициентов системы.

→ →

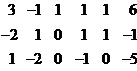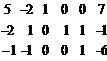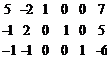
Получили систему ограничений с единичным базисом (х₃; х₄; х₅):

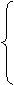
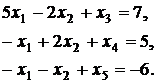
Отбрасывая базисные переменные, получим стандартную задачу ЛП: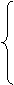

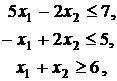
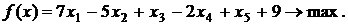
Выразим функцию цели через свободные неизвестные х₁ и х₂. Имеем:

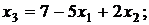
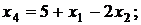
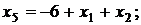
тогда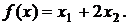

Решим задачу геометрическим способом, как показано в разделе 2. Область планов представляет собой треугольник АВС и функция цели достигает максимального и минимального значения в его вершинах:

Из рисунка видно, что точка В(3, 4) − точка максимума, тогда:

f(X_опт) = 3 + 2·4 = 11.

Для решения задачи симплекс-методом приведем систему ограничений к каноническому виду методом искусственного базиса. Заменив знаки в третьем ограничении, сделаем правые части уравнений неотрицательными:

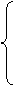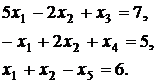
Очевидно, что в третьем уравнении нет базисной переменной. Используем метод искусственного базиса. Введем в это уравнение вспомогательную переменную ξ. Теперь решим вспомогательную задачу по минимизации функции 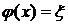симплекс-методом.

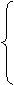
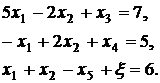
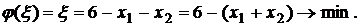
Занесем эту задачу в таблицу

Таблица 1

Б	В	х1	х2	х3	х4	х5	ξ
x3			-2
x4		-1
ξ						-1

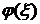Введем в базис х₂, тогда из базиса выйдет переменная х₄. Пересчитывая таблицу, получим:

Таблица2

Б	В	х1	х2	х3	х4	х5	ξ
x3
x2	2.5	-0.5			0.5
ξ	3.5	1.5			-0.5	-1
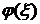	3.5	1.5			-0.5	-1

Введем в базис х₁, тогда из базиса выйдет переменная ξ. Пересчитывая таблицу, получим:

Таблица 3

Б	В	х1	х2	х3	х4	х5	ξ
x3	8/3				7/3	8/3	-8/3
x2	11/3				1/3	-1/3	1/3
x1	7/3				-1/3	-2/3	2/3
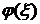							-1

Данная таблица - завершающая таблица метода, она содержит оптимальный план вспомогательной задачи. Поскольку, 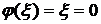, то, отбрасывая последний столбец, получаем каноническую систему для исходной задачи.

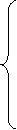
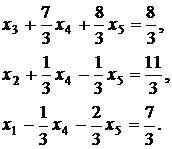
Выразим функцию цели через свободные переменные:

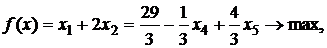
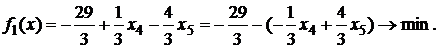
и решим исходную задачу симплекс-методом.

Б	В	х1	х2	х3	х4	х5
x3	8/3				7/3	8/3
x2	11/3				1/3	-1/3
x1	7/3				-1/3	-2/3
f1(X)	-29/3				-1/3	4/3

Выполняя преобразования, получаем оптимальный план, доставляющий минимум функции цели f₁(X) .

Б	В	х1	х2	х3	х4	х5
x5				0.375	0.875
x2				0.25	0.25
x1				0.125	0.625
f1(X)	-11			-0.5	-1.5

Получен оптимальный план. Запишем ответ

Х_опт = (3; 4; 0; 0;1);

f₁(X_опт) = -11 (min), тогда f₁(X_опт) = 11 (max).

Индивидуальные задания

Задание 1

Предприятие выпускает два вида продукции А₁ и А₂, используя при этом три вида сырья S₁, S₂ и S₃. Известны запасы сырья равные b₁, b₂ и b₃ соответственно. Расход сырья вида S_i на производство единицы продукции A_j равен a_i,j. Доход от реализации единицы продукции A_j составляет c_j условных единиц. Требуется составить такой план производства продукции, при котором доход будет максимальным.

Решить задачу графическим методом; составить каноническую модель данной задачи и решить ее симплекс-методом. Найти двойственные оценки цен на сырье, из решения симметричной двойственной задачи по теоремам двойственности.

Вариант 1.
	А1	А2	bi
B1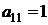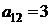
B2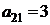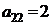
B3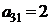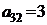
cj

Вариант 2.
	А1	А2	bi
B1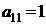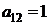
B2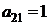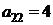
B3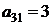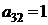
cj

Вариант 3.
	А1	А2	bi
B1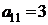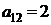
B2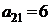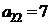
B3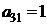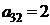
cj

Вариант 4.
	А1	А2	bi
B1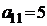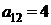
B2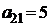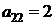
B3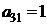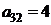
cj

Вариант 5.
	А1	А2	bi
B1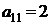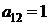
B2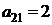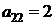
B3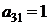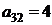
cj

Вариант 6.
	А1	А2	bi
B1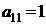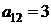
B2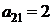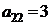
B3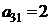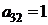
cj

Вариант 7.
	А1	А2	bi
B1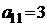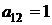
B2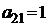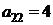
B3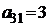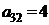
cj

Вариант 8.
	А1	А2	bi
B1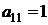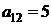
B2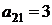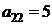
B3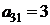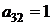
cj

Вариант 9.
	А1	А2	bi
B1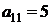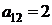
B2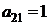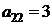
B3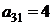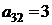
cj

Вариант 10.
	А1	А2	bi
B1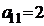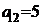
B2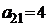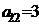
B3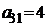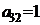
cj

Задание 2

Дана основная задача линейного программирования. При помощи элементарных преобразований матрицы коэффициентов системы ограничений, привести задачу к стандартному виду и решить ее геометрическим методом. Методом искусственного базиса получить каноническую задачу (или доказать несовместность этой системы). Решить полученную модель с помощью симплекс- таблиц (или доказать, что она не имеет оптимального плана).

Вариант 1

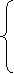
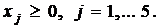
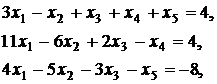
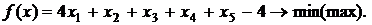
Вариант 2

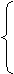
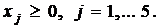
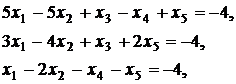
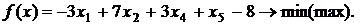
Вариант 3

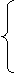
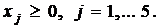
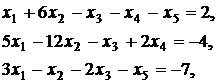
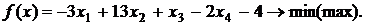
Вариант 4

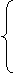
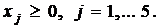
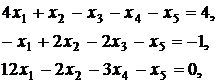
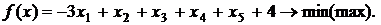
Вариант 5

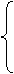
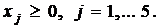
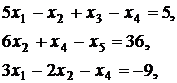
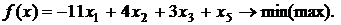
Вариант 6

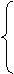
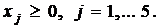
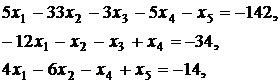
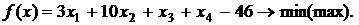
Вариант 7

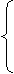
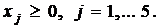
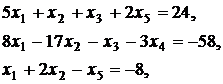
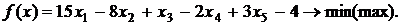
Вариант 8

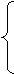
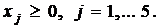
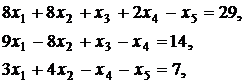
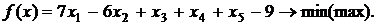
Вариант 9

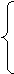
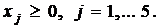
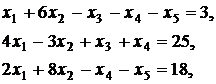
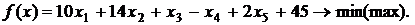
Вариант 10