Упорядоченная совокупность элементов

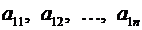– первая строкаматрицы,

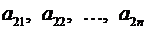– вторая строка и т.д.,

Упорядоченная совокупность элементов

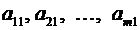– первый столбец,

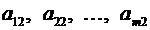– второй столбец и т.д.

В печатном тексте матрицы обозначаются прописными буквами латинского алфавита.

Для матрицы приняты также следующие обозначения:

.

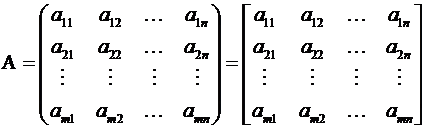Употребляются и более краткие обозначения

.

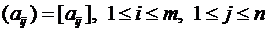В дальнейшем будем пользоваться обозначением матрицы с круглыми скобками.

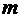Матрицу, имеющую строк и 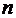столбцов, называют матрицей типа 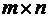(читается « »).

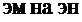В отдельных случаях употребляется также термин «размер матрицы».

То, что матрица 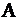имеет тип 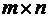, обозначается следующим

образом: .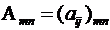

Две матрицы, имеющие одинаковое количество строк и столбцов, называются матрицами одинакового типа.

Если 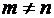, матрица называется прямоугольной.

Квадратная матрица

Квадратной называется матрица, у которой число строк равно числу столбцов 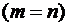, т.е. матрица вида

.

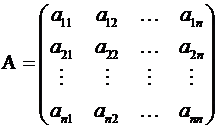В этом случае число 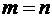называют порядком квадратной матрицы.

Квадратная матрица 1-го порядка отождествляется со своим единственным элементом, например (17).

При этом следует обратить внимание на то, что она является иным математическим объектом, чем вещественное число 17, и поэтому должна изображаться числом, заключенным в скобки.

Выпишем квадратные матрицыпервых трех порядков:

.

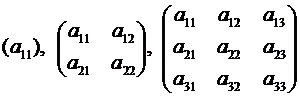Ø Элементы квадратной матрицы, имеющие одинаковые значения индексов

,

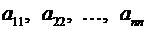составляют главную диагональ,

Ø а элементыквадратной матрицы порядка 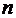, сумма индексов каждого из которых равна 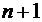, – побочную (или вторую) диагональ,

.

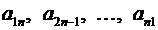Сумма элементов главной диагонали квадратной матрицы называется следомматрицы.

ОПРЕДЕЛИТЕЛИ

Определители второго и третьего порядков

С понятиемматрицытесно связано понятиеопределителя.

Понятиеопределителя возникло в связи с проблемой отыскания формул, чтобы найти значения неизвестных в системелинейных уравнений.

Рассмотрим системудвух линейных уравненийс двумянеизвестными:

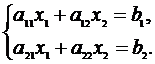(2.1)

Чтобы найти неизвестное ,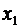

Ø умножим первое уравнение на величину ,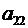

Ø а второе на величину .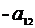

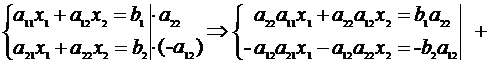
Складывая, полученные левые и правые части, получим

.

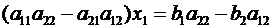Аналогично, умножаяпервое уравнение на 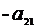, второе ,

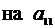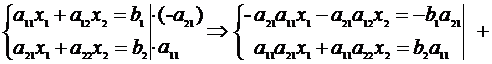
Найдём

.

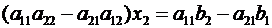Предполагая, что 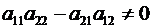, получаем

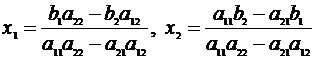. (2.2)

Непосредственной проверкой легко убедиться, что значения для неизвестных 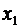и 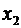, даваемые формулами (2.2), действительно удовлетворяют системе (2.1).

Таким образом, доказано, что если 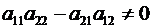, то система (2.1) имеет единственное решение, определяемое формулами (2.2).

Рассмотрим квадратную матрицу 2-го порядка, составленную из коэффициентов при неизвестных 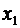и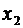

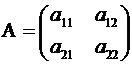, (2.3)

Определение. Определителем квадратной матрицы 2-го порядка (2.3) называется число 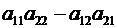, вычисляемое по следующему правилу:

надо взять произведение чисел, расположенных по главной диагонали (диагональ, идущая от левого верхнего угла к правому нижнему углу),

и вычесть из него произведение чисел, расположенных на побочной диагонали (диагональ, идущая от правого верхнего элемента к левому нижнему).

Для определителя, как и для матрицы, используются такие понятия, как элемент, строка, столбец, главная и побочная диагональ и т.п.

Определитель квадратной матрицы 2-го порядка кратко называют определителем или детерминантом 2-го порядка.

Определитель квадратной матрицы (2.3) обозначается двумя вертикальными черточками:

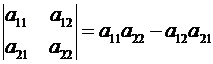. (2.4)

Кроме того, для определителя матрицы (1.3) применяются

обозначения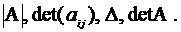

(От французского слова determinant.)

Правило, по которому вычисляется определительматрицы 2-го порядка, схематически можно изобразить следующим образом:

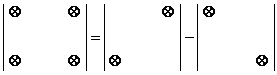или

– +

Пример. Вычислить определитель матрицы .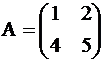

▲ . ▼

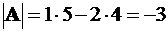Приняв введённое определение определителя 2-го порядка, замечаем, что числители в формулах (2.2) могут быть представлены

теперь в виде

,

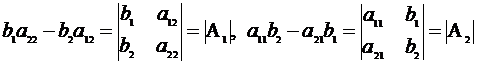где матрицы 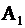и 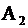получаются из матрицы 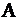заменой первого, соответственно второго, столбца на свободные члены.

Формулы (2.2) принимают теперь следующий вид:

.

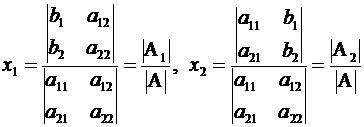Напомним еще раз, что эти формулы применимы лишь в случае, когда .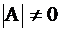

Рассмотрим теперь систему трех линейных уравнений с тремя неизвестными

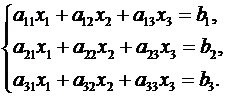(2.5)

Чтобы найтинеизвестное 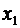, умножим уравнения системы (2.5) соответственно на выражения

,

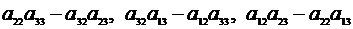и сложим, полученные левые и правые части.

После приведения подобных членов (относительно 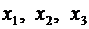) окажется, что коэффициенты при неизвестных 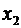и 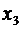равны нулю.

Предполагая, что коэффициентпри неизвестном 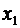отличенот нуля, получим

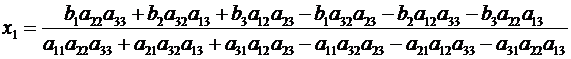. (2.6)

Рассмотрим квадратную матрицу 3-го порядка

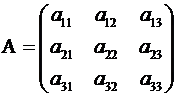. (2.7)

Матрица 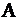составлена из коэффици..ентов при неизвестных .

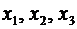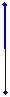
Определение. Определителем квадратной матрицы 3-го порядка (2.7) называется число

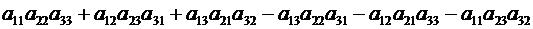
Определитель матрицы (2.7) кратко называют определителем 3-го порядка и обозначают двумя вертикальными чертами или одним из символов .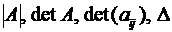

Итак, по определению

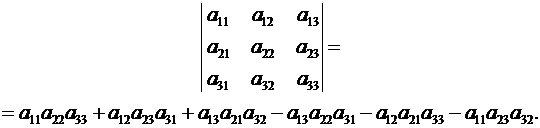(2.8)

Таким образом,

каждый членопределителя 3-го порядка представляет собой произведение трёх его элементов, взятых по одному из каждой строки и каждого столбца.

Эти произведения берутся с определенными знаками.

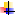Со знаком плюс – три члена, состоящие из элементов главной диагонали и из элементов, расположенных в вершинах равнобедренных треугольников с основаниями, параллельными главной диагонали, и с вершиной в противоположном углу.

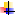Со знаком минус – три члена, расположенные аналогичным образом относительно побочной диагонали.

Схематически это правило (правилоСаррюса или правилотреугольников) может быть изображено следующим образом:

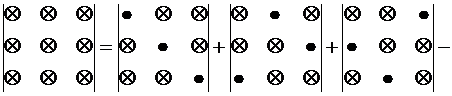
или

+ –

Пьер Фредерик Саррюс – французский математик.

Саррюс поступил на факультет естественных наук, окончив его со специализацией в математике в 1821 году.

С 1826 г. он преподавал в Страсбургском университете, с 1829 г. был профессором, в 1839‒1852 гг. деканом.

В 1858 г. по болезни вышел в отставку.

Пример. Вычислить определитель матрицы .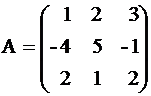

▲

. ▼

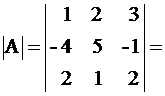
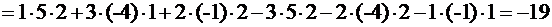Итак, знаменатель в формуле (2.6) представляется в виде определителя .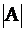

Что касается числителя, то, поскольку он получается из знаменателя заменой чисел 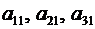соответственно на числа 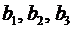– его можно представить в виде определителя

.

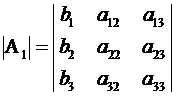Аналогичным образом, если уравнения системы (2.5) умножим последовательно на выражение

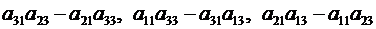
и результаты сложим, найдём формулу для неизвестного .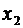

Наконец, умножая уравнения (2.5) последовательно на выражения

,

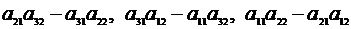найдем формулу для неизвестного .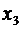

Окончательно будем иметь

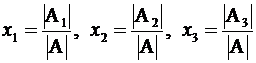, (2.9)

где матрицы 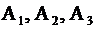получаются из матрицы 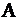заменой соответствующего столбца на свободные члены.

Если квадратная матрица 3-го порядка является треугольной, т.е. имеет вид

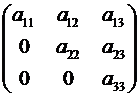или ,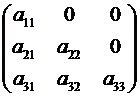

то её определитель равен произведению элементов главной диагонали, т.е.

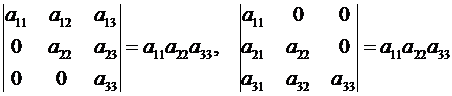. (2.10)

Равенства (2.10) следуют из формулы (2.8).

Свойства определителей

Вычислениеопределителей значительно облегчается, если пользоваться их свойствами.

Будем излагать свойстваопределителейна примереопределителей третьего порядка.