Тема 10. случайные события, случайные величины, элементы математической статистики

Задание 1. Бросают две монеты. Найти вероятность того, что:

1. на обеих монетах появится «герб»,

2. хотя бы на одной монете появится «герб»;

3. ни на одной монете не появится «герб»;

Бросают три монеты. Найти вероятность того, что:

4. на всех монетах появится «герб»;

5. хотя бы на одной монете появится «герб»;

6. только на двух монетах появится «герб»;

7. только на одной монете появится «герб»;

8. ни на одной монете не появится «герб».

Бросают четыре монеты. Найти вероятность того, что:

9. на всех монетах появится «герб»;

10. хотя бы на одной монете появится «герб»;

11. только на одной монете появится «герб»;

12. только на двух монетах появится «герб»;

13. только на трех монетах появится «герб»;

14. ни на одной монете не появится «герб».

Бросают игральную кость. Найти вероятность того, что на верхней грани появится:

15. четное число очков;

16. «1» или «6».

Бросают две игральные кости. Найти вероятность того, что на верхних гранях появятся следующие числа очков:

17. только четные;

18. одно четное, другое нечетное;

19. сумма которых четна;

20. сумма которых нечетна;

21. сумма которых больше, чем их произведение;

22. сумма которых меньше шести;

23. сумма которых больше восьми.

Бросают три игральные кости. Найти вероятность того, что на верхних гранях появятся следующие числа очков

24. только четные;

25. одно четное, остальные нечетные;

26. сумма которых четна;

27. сумма которых нечетна;

28. которые все одинаковы;

29. которые все различны;

30. сумма которых делится на четыре;

31. сумма которых делится на пять.

32. только четные.

Пример. Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять.

Решение. Определим испытание и его результат, то есть элементарное событие. Испытанием является бросание трех игральных костей; результатом – одно из сочетаний очков 1, ..., 6 на верхних гранях трех костей.

Исследуемое событие А – сумма очков на трех костях делится на пять. Вероятность события А вычислим с помощью формулы:

.

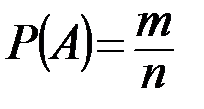Общее количество элементарных событий п можно найти по правилу умножения. На каждой игральной кости 6 граней и все они могут сочетаться со всеми гранями других костей. Итак, получаем .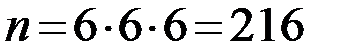

Количество элементарных событий т, входящих в состав события А или благоприятствующих событию А,найдем выписав всевозможные результаты испытаний и оставив из них только те, для которых сумма очков на всех трех костях делится на пять. Можно облегчить работу, выписав всевозможные исходы бросания первых двух костей, сочетая с ними подходящие значения количества очков, выпавших на третьей кости. Имеем:

В результате получаем, что 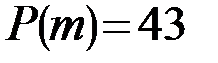, значит, .

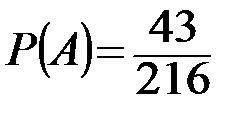Ответ: .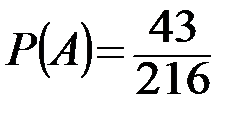

Задание 2.

Варианты 1-8.

В семье n детей. Считая вероятности рождения мальчика и девочки одинаковыми, найти вероятности следующих событий:

а) в семье m мальчиков и k девочек;

б) число мальчиков в семье от m₁ до m_{2 .}

№ варианта	n	m	k	m1	m2

Варианты 9-16.

На заводе работает линия из n однотипных станков. Вероятность поломки одного станка в течение смены р. Найти вероятности следующих событий:

а) в течение одной смены сломается m станков;

б) число сломанных станков в течение одной смены будет в пределах от m₁ до m₂

№ варианта	n	р	m	m1	m2
		0,2
		0,3
		0,1
		0,2
		0,1
		0,2
		0,3
		0,2

Варианты 17-24.

Игральная кость бросается n раз. Найти вероятности следующих событий:

а) «шестерка» выпадет m раз;

б) число выпадений «шестерки» будет в пределах от m₁ до m_{2 .}

№ варианта	n	m	m1	m2

Варианты 25-32.

При передаче сообщения вероятность искажения одного знака р. Переданное сообщение содержит в себе n знаков. Найти вероятности следующих событий:

а) в переданном сообщении искажено m знаков;

б) число искаженных знаков в переданном сообщении от m₁ до m_2.

№ варианта	n	р	m	m1	m2
		0,2
		0,2
		0,1
		0,3
		0,3
		0,4
		0,5
		0,3

Пример.Вероятность выигрыша по одному билету равна 0,2. Имеется шесть билетов. Найти вероятности следующих событий:

а) два билета будут выигрышными;

б) выигрышных билетов будет от двух до четырех.

Решение. Для вычисления искомых вероятностей воспользуемся формулой Бернулли:

.

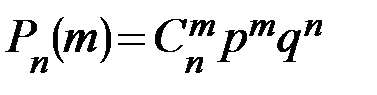По условию задачи , .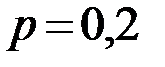

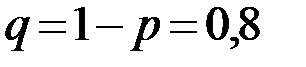а) Рассмотрим случайное событие А: два билета из шести будут выигрышными. Его вероятность: .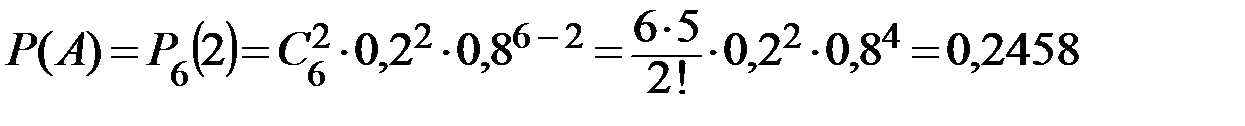

б) Рассмотрим случайное событие В: выигрышных билетов будет от двух до четырех. Это сложное событие состоит из следующих:

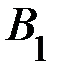: два билета из шести будут выигрышными;

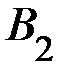: три билета из шести будут выигрышными;

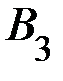: четыре билета из шести будут выигрышными.

Тогда 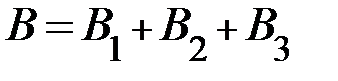и .

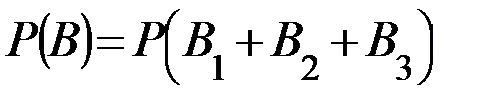Находим по формуле Бернулли соответствующие вероятности:

,

,

.

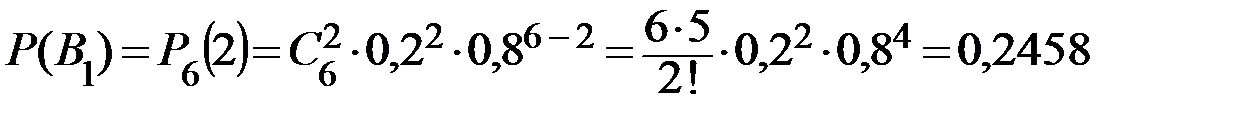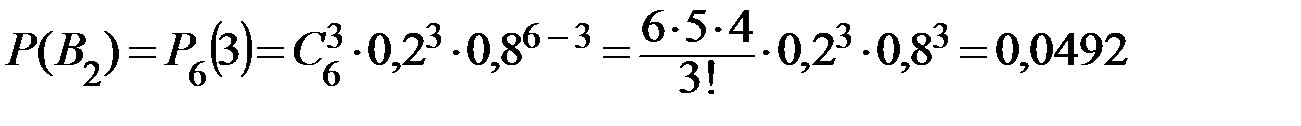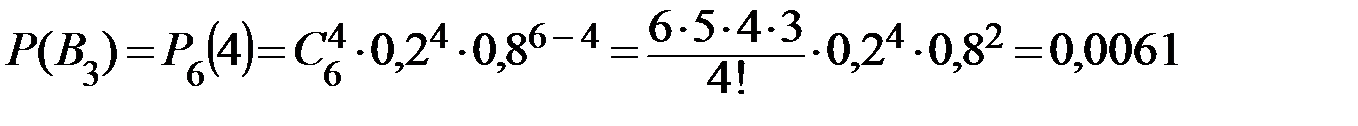Тогда искомая вероятность: .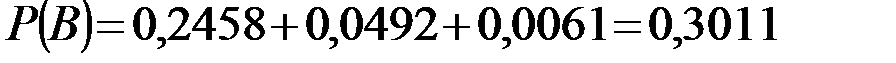

Ответ: .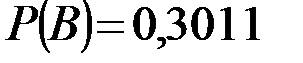

Задание 3. Случайная величина X задана рядом распределения:

X	x1	x2	x3	x4
p	p1	p2	p3	p4

Найти функцию распределения F(x) и построить её график. Вычислить для Х её среднее значение M(X),дисперсию D(X) и среднеквадратическое отклонение .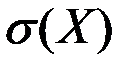

№ варианта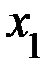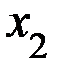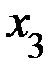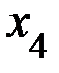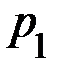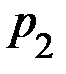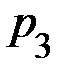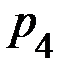
					0,143	0,2	0,49	0,167
					0,143	0,2	0,49	0,167
					0,143	0,2	0,49	0,167
					0,143	0,2	0,49	0,167
					0,125	0,167	0,508	0,2
					0,111	0,143	0,496	0,25
					0,1	0,125	0,442	0,333
					0,143	0,2	0,49	0,167
					0,125	0,167	0,508	0,2
					0,111	0,143	0,496	0,25
					0,1	0,125	0,442	0,333
					0,143	0,2	0,49	0,167
					0,125	0,167	0,508	0,2
					0,111	0,143	0,496	0,25
					0,1	0,125	0,442	0,333
					0,143	0,2	0,49	0,167
					0,125	0,167	0,508	0,2
					0,111	0,143	0,496	0,25
					0,1	0,125	0,442	0,333
					0,143	0,2	0,49	0,167
					0,125	0,167	0,508	0,2
					0,111	0,143	0,496	0,25
					0,1	0,125	0,442	0,333
					0,143	0,2	0,49	0,167
					0,125	0,167	0,508	0,2
					0,111	0,143	0,496	0,25
					0,1	0,125	0,442	0,333
					0,143	0,2	0,49	0,167
					0,125	0,167	0,508	0,2
					0,111	0,143	0,496	0,25
					0,1	0,125	0,442	0,333
					0,143	0,2	0,49	0,167

Пример.

X	3	5	7	11
P	0,14	0,20	0,49	0,17

Решение. Функцию распределения находим по формуле:

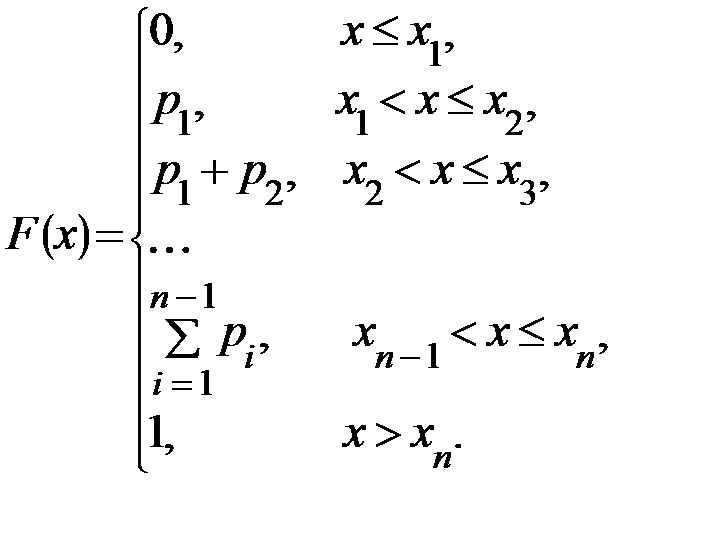
Тогда:

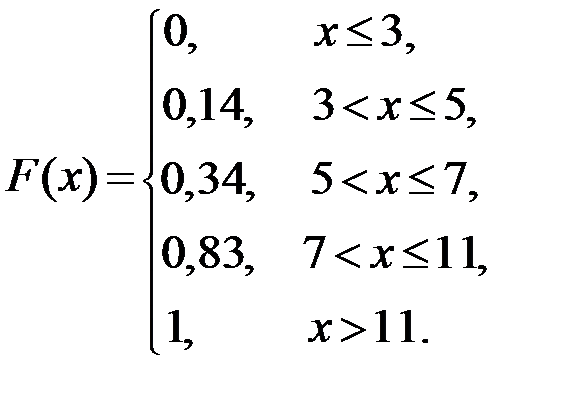
Построим график функции распределения F(x) (см. рисунок).

Среднее значение М(Х) вычисляем по формуле :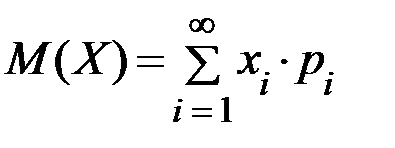

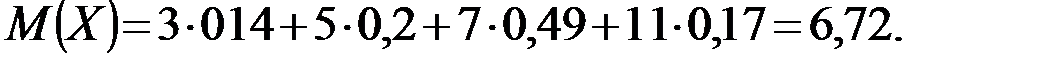
Для нахождения дисперсии воспользуемся формулам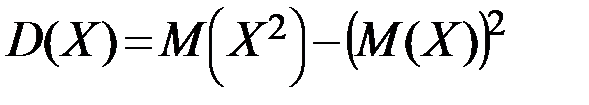и и :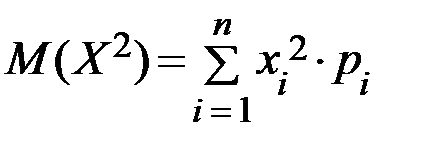

.

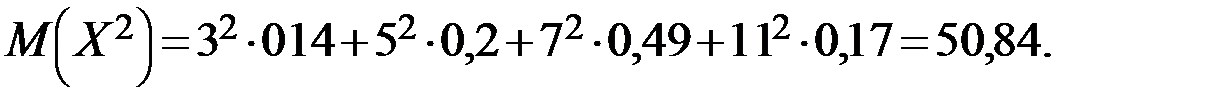
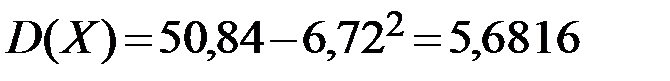Среднеквадратическое отклонение 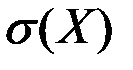находим по формуле :

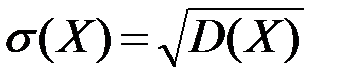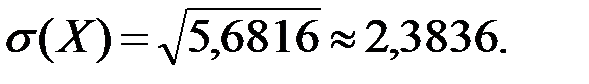
F(x)

0,5

3 5 7 11 х

Рис. График функции распределения.

Ответ:

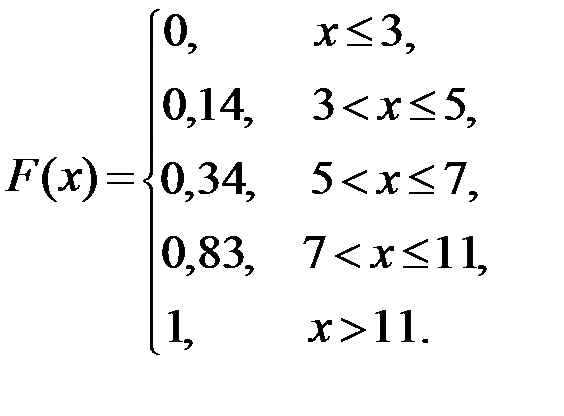
M(X)=6,72, D(X)=5, 6816,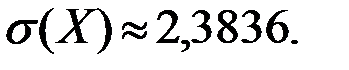

Задание 4. После обработки результатов эксперимента составлена таблица, в первой строке которой указаны группы возможных значений некоторой случайной величины х _i , а во второй строке – численность каждой группы значений m _i . Найти объем выборки n;относительные частоты 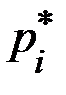, соответствующие каждой отдельной группе значений случайной величины; составить вариационный ряд распределения данной случайной величины. Найти числовые характеристики выборки: среднее арифметическое, выборочную дисперсию и среднеквадратическое отклонение.

Вариант 1.

х i
m i

Вариант 2.

х i
m i

Вариант 3.

х i
m i

Вариант 4.

х i
m i

Вариант 5.

х i
m i

Вариант 6.

х i
m i

Вариант 7.

х i
m i

Вариант 8.

х i
m i

Вариант 9.

х i
m i

Вариант 10.

х i
m i

Вариант 11.

х i
m i

Вариант 12.

х i
m i

Вариант 13.

х i
m i

Вариант 14.

х i
m i

Вариант 15.

х i
m i

Вариант 16.

х i
m i

Вариант 17.

х i
m i

Вариант 18.

х i
m i

Вариант 19.

х i
m i

Вариант 20.

х i
m i

Вариант 21.

х i
m i

Вариант 22.

х i
m i

Вариант 23.

х i
m i

Вариант 24.

х i
m i

Вариант 25.

х i
m i

Вариант 26.

х i
m i

Вариант 27.

х i
m i

Вариант 28.

х i
m i

Вариант 29.

х i
m i

Вариант 30.

х i
m i

Вариант 31.

х i
m i

Вариант 32.

х i
m i

Пример. После обработки результатов эксперимента составлена таблица, в первой строке которой указаны группы возможных значений некоторой случайной величины х _i , а во второй строке – численность каждой группы значений m _i :

х i
m i

Решение. Найдем объем выборки n по формул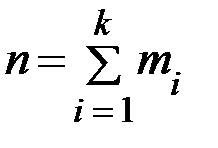е: , где 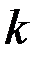– число столбцов в таблице. Тогда n =3+11+14+5=33.

Относительные частоты 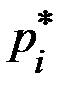, соответствующие каждой отдельной группе значений случайной величины, находим по формулам: 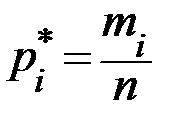. Получаем: , , , .

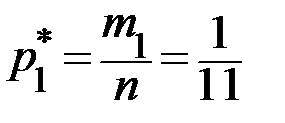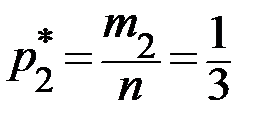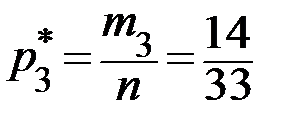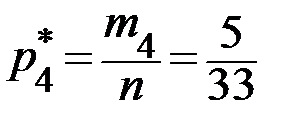Составим вариационный ряд распределения данной случайной величины:

х i

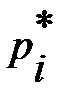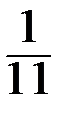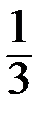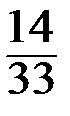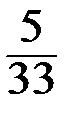Находим числовые характеристики выборки:

а) среднее арифметическое находим по формуле: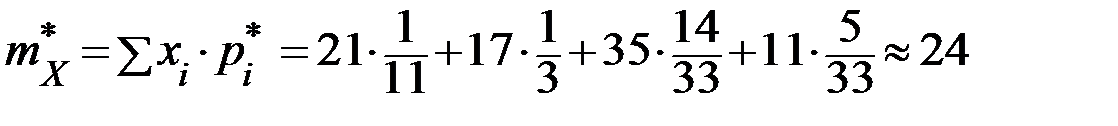

б) выборочная дисперсия находится по формуле: .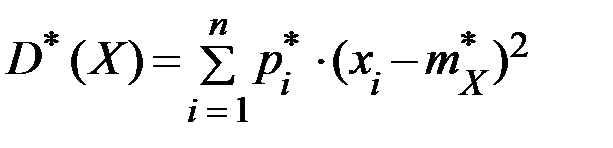

Получаем: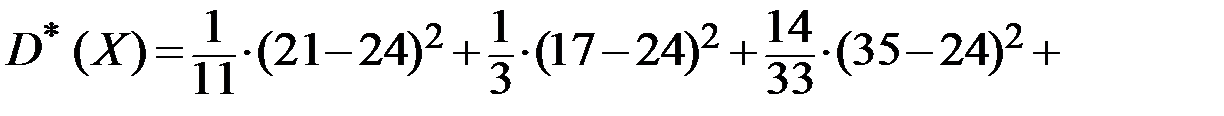

.

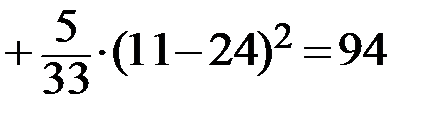в) среднеквадратическое отклонение: .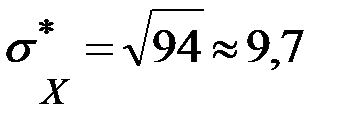

ЛИТЕРАТУРА

1. Баврин, И. И. Высшая математика / И. И. Баврин. М.: Издательский центр «Академия». 2003.

2. Гмурман, В. Е. Теория вероятностей и математическая статистика / В. Е. Гмурман. М.: Высшая школа. 2004.

3. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике / В. Е. Гмурман. М.: Высшая школа, 1997.

4. Данко, П. Е. Высшая математика в примерах и задачах / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. Часть 1, 2. М.: Высшая школа. 2009.

5. Ефимов, Н. В. Краткий курс аналитической геометрии / Н. В. Ефимов. М.: ФИЗМАТЛИТ, Лаборатория Базовых Знаний. 2003.

6. Лунгу, К. Н. Сборник задач по высшей математике / К. Н. Лунгу, Д. Т. Письменный, С. Н. Федин, Ю. А. Шевченко. 1 курс. М.: Айрис-пресс. 2003.

7. Пискунов, Н. С. Дифференциальное и интегральное исчисления / Н. С. Пискунов. М.: «Интеграл – Пресс», т. 1, 2. 2007.

8. Сборник типовых расчётов по высшей математике / Под редакцией В. Б. Миносцева. М.: МГИУ. 2001.