Тема 2. аналитическая геометрия
НА ПЛОСКОСТИ
Задание 1Даны вершины треугольника АВС: 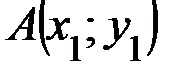 ,
, 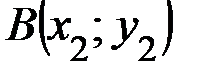 ,
, 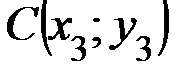 .
.
Найти:
1. Периметр треугольника АВС.
2. Уравнения всех сторон треугольника в общем виде.
3. Уравнение высоты СН.
4. Уравнение медианы АМ.
| № варианта | А | В | С |
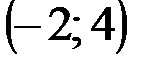 | 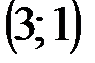 | 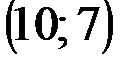 | |
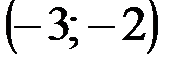 | 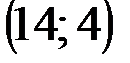 | 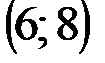 | |
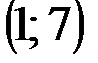 | 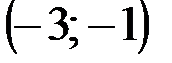 | 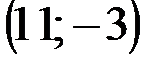 | |
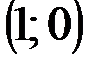 | 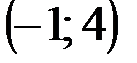 | 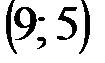 | |
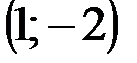 | 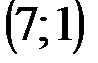 | 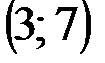 | |
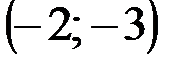 | 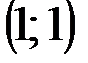 | 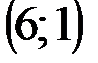 | |
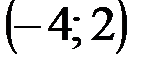 | 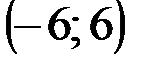 | 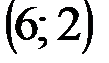 | |
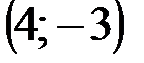 | 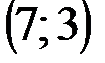 | 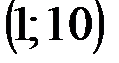 | |
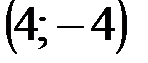 | 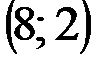 | 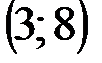 | |
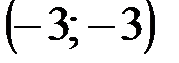 | 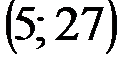 | 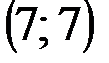 | |
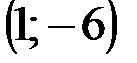 | 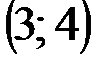 | 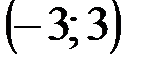 | |
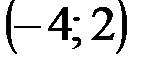 | 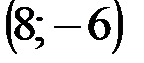 | 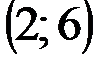 | |
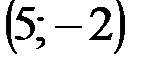 | 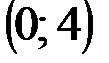 | 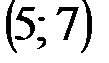 | |
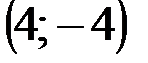 | 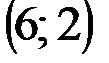 | 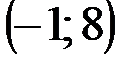 | |
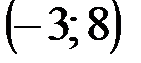 | 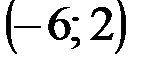 | 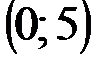 | |
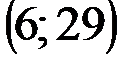 | 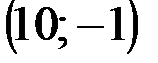 | 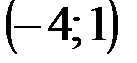 | |
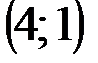 | 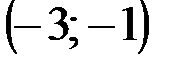 | 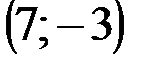 | |
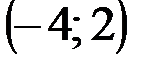 | 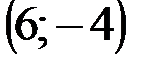 | 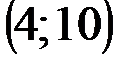 | |
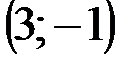 | 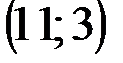 | 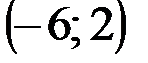 | |
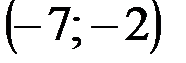 | 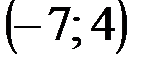 | 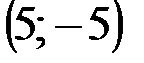 | |
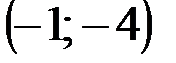 | 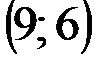 | 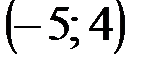 | |
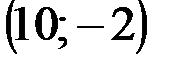 | 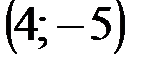 | 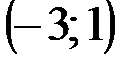 | |
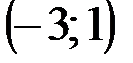 | 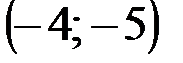 | 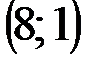 | |
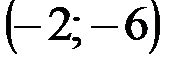 | 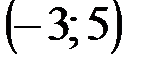 | 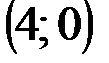 | |
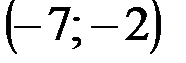 | 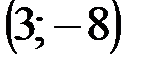 | 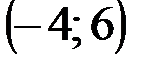 | |
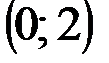 | 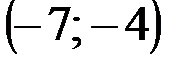 | 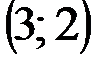 | |
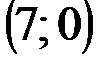 | 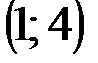 | 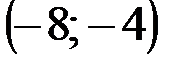 | |
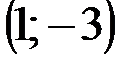 | 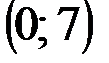 | 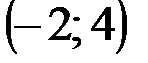 | |
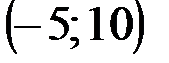 | 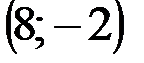 | 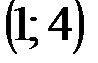 | |
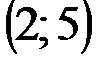 | 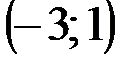 | 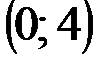 | |
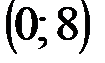 | 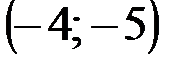 | 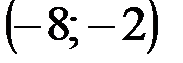 | |
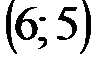 | 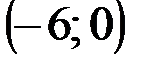 | 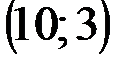 |
Пример. 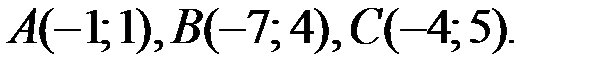
Решение.
1. Вычислим длины всех сторон треугольника, применяя формулу нахождения расстояния между двумя точками 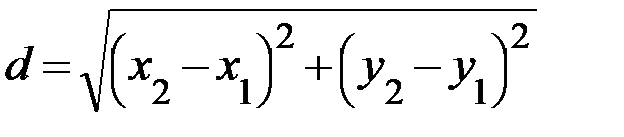 :
:
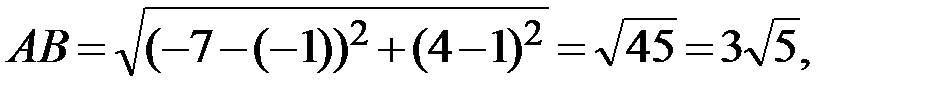
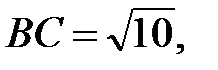
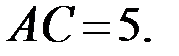
Следовательно, периметр треугольника ABC равен 
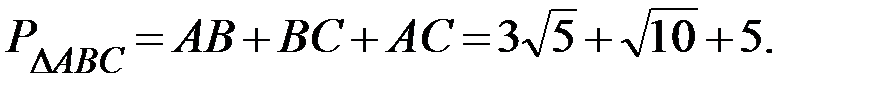
Ответ: 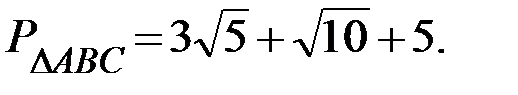
2. Составим общее уравнение прямой AB. Для этого воспользуемся уравнением прямой, проходящей через две точки:
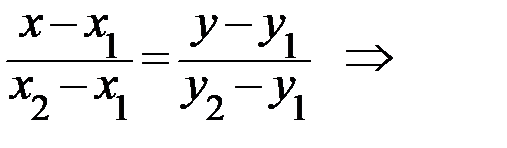
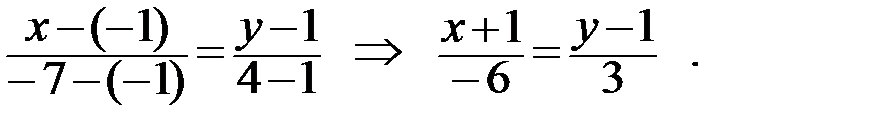
Преобразуем полученное уравнение к общему уравнению прямой Ax+By+C=0. Для этого избавимся от дробей, применив, например, правило пропорции: 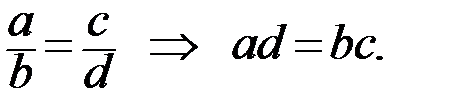 Получаем следующий результат
Получаем следующий результат 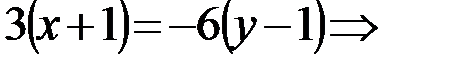
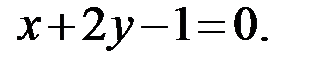
Аналогично находим уравнения сторон BC: 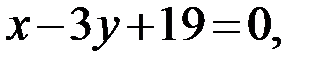 AC:
AC: 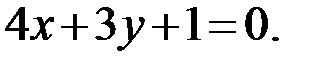
Ответ: AB: 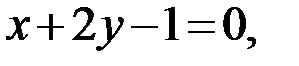 BC:
BC: 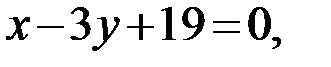 AC:
AC: 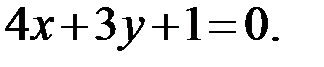
4.Для нахождения уравнения высоты CH воспользуемся уравнением прямой с данным угловым коэффициентом и проходящей через данную точку: 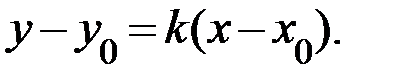 Известно, что условием перпендикулярности двух прямых является следующее равенство:
Известно, что условием перпендикулярности двух прямых является следующее равенство: 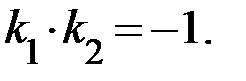 Так как прямые AB и CH перпендикулярны, то
Так как прямые AB и CH перпендикулярны, то 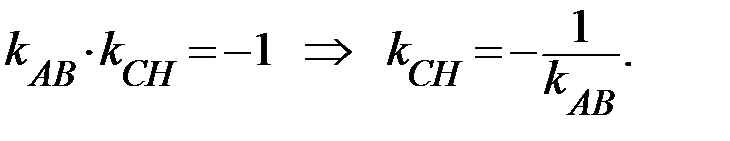
Для нахождения углового коэффициента 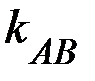 прямой АВ воспользуемся общим уравнением прямой АВ:
прямой АВ воспользуемся общим уравнением прямой АВ: 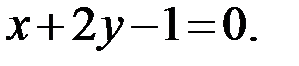 Преобразуем это уравнение к уравнению прямой с угловым коэффициентом: y=kx+b. Для этого из общего уравнения прямой АВ выразим у:
Преобразуем это уравнение к уравнению прямой с угловым коэффициентом: y=kx+b. Для этого из общего уравнения прямой АВ выразим у: 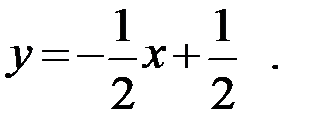 Тогда
Тогда 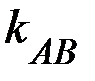 равен коэффициенту перед х в уравнении прямой с угловым коэффициентом, то есть
равен коэффициенту перед х в уравнении прямой с угловым коэффициентом, то есть 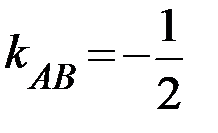 . И тогда
. И тогда 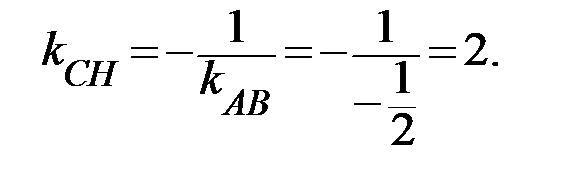
Используя координаты точки С, получаем уравнение высоты СH: 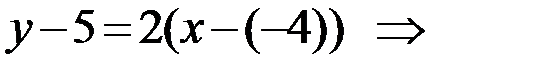
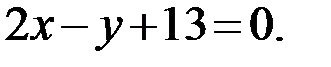
Ответ: CH: 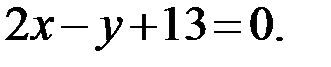
4. Используя формулы для нахождения координат середины отрезка (полусумма соответствующих координат), найдем координаты точки M: 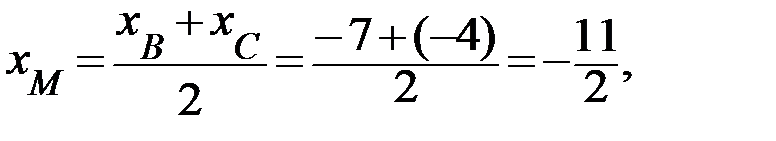
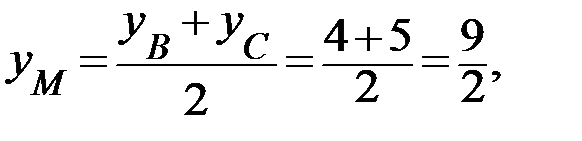 тогда
тогда 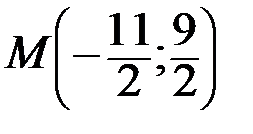 . Используя уравнение прямой, проходящей через две точки A и M, получим уравнение медианы AM:
. Используя уравнение прямой, проходящей через две точки A и M, получим уравнение медианы AM:
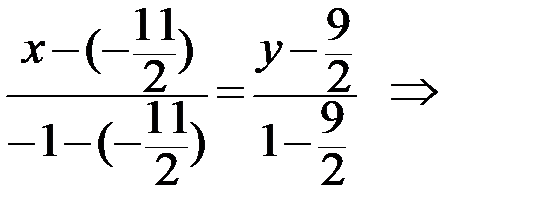
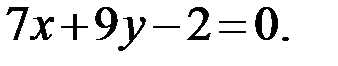
Ответ: AM: 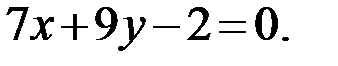
Задание 2. Привести уравнение кривой второго порядка к каноническому виду, определить геометрический образ и построить кривую.
1. 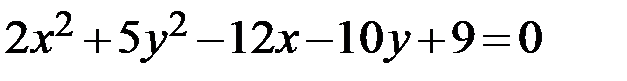
2. 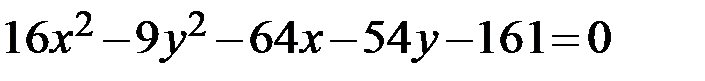
3. 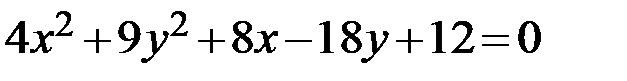
4. 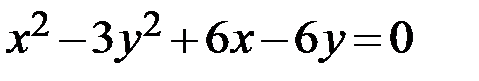
5. 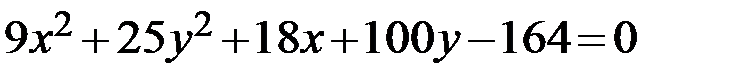
6. 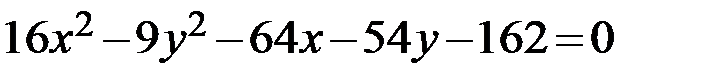
7. 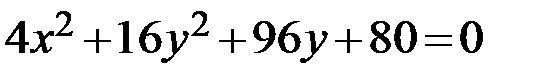
8. 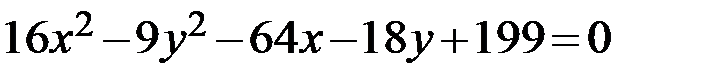
9. 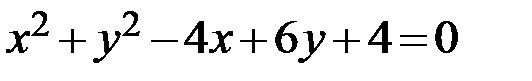
10. 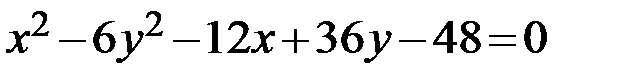
11. 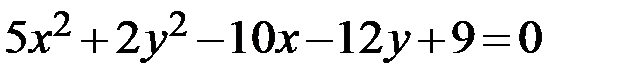
12. 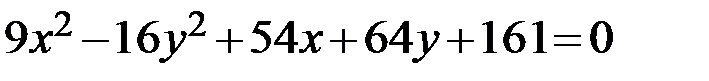
13. 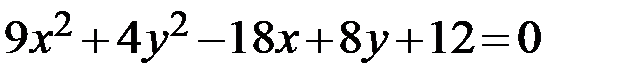
14. 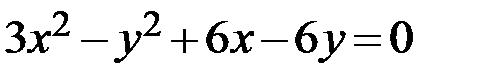
15. 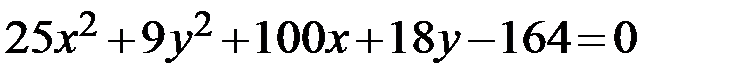
16. 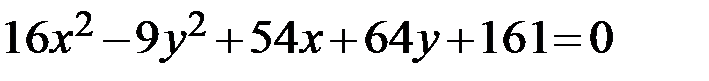
17. 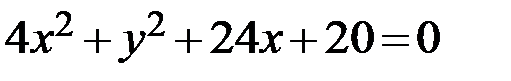
18. 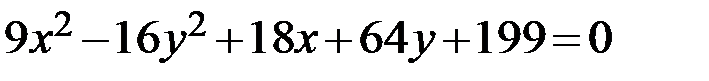
19. 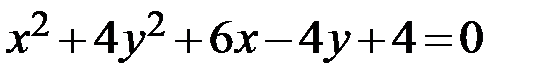
20. 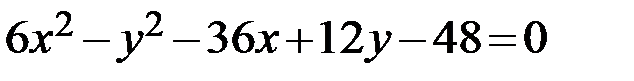
21. 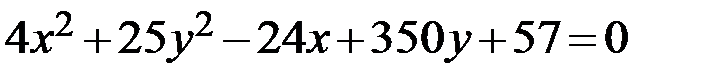
22. 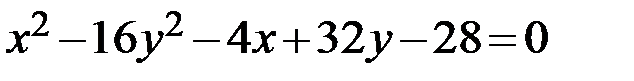
23. 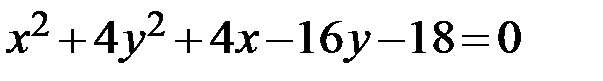
24. 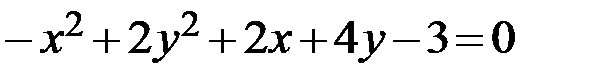
25. 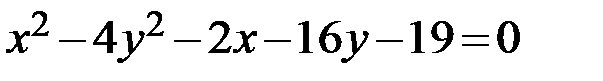
26. 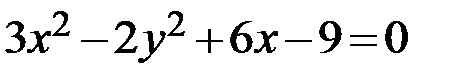
27. 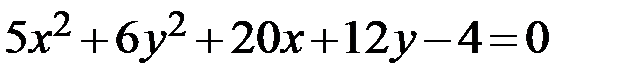
28. 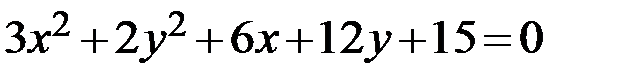
29. 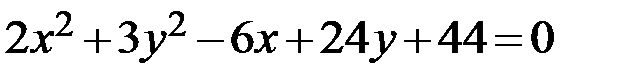
30. 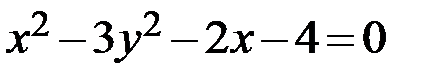
31. 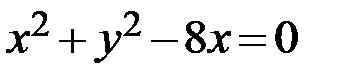
32. 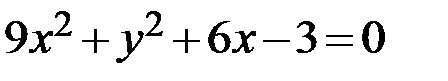
Пример. 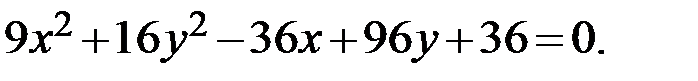
Решение. Сгруппируем слагаемые с одинаковыми неизвестными:
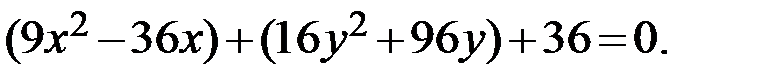
Коэффициенты перед 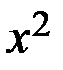 и
и 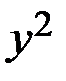 вынесем за скобку:
вынесем за скобку:
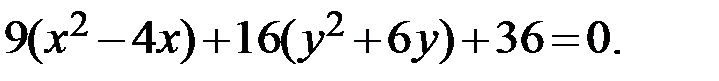
Дополним выражения относительно xи yдо полного квадрата:
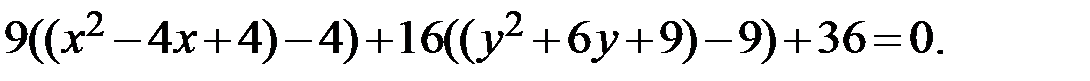
Свернём полный квадрат:
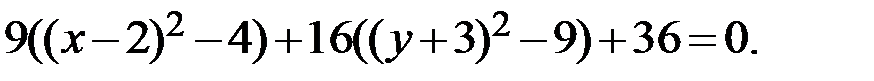
Раскроем внешние скобки:
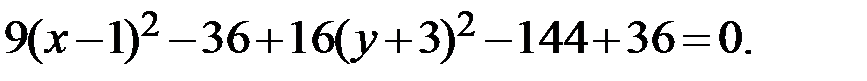
Слагаемые с квадратами оставляем в левой части уравнений, остальные переносим в правую часть:
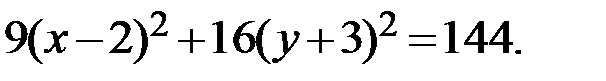
Разделив обе части последнего уравнения на 144, получим:
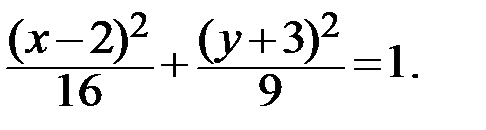
Далее применяем формулы преобразования координат при параллельном сдвиге осей, то есть переходим к новой системе координат 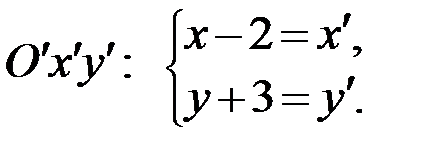
Здесь 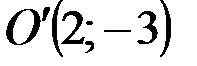 – новое начало координат и
– новое начало координат и 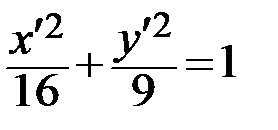 – каноническое уравнение.
– каноническое уравнение.
Полученное уравнение является каноническим уравнением эллипса с центром в точке 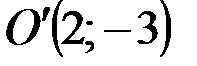 и полуосями
и полуосями 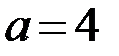 ,
, 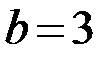 . Рисунок приведён ниже.
. Рисунок приведён ниже.
| –2 |
| –3 |
| –6 |
| x |
| y |
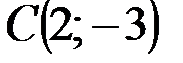  |
 |
 |
Ответ: 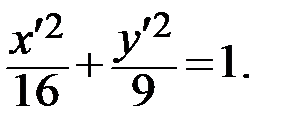 Данное уравнение кривой второго порядка определяет эллипс с центром в точке
Данное уравнение кривой второго порядка определяет эллипс с центром в точке 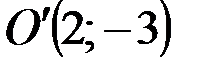 и полуосями
и полуосями 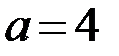 ,
, 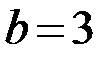 .
.
ТЕМА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
В ПРОСТРАНСТВЕ
Задание 1. Даны координаты точек: 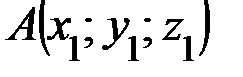 ,
, 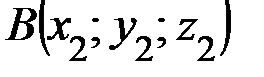 ,
, 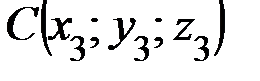 ,
, 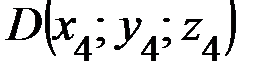 .
.
Найти:
1. Координаты векторов 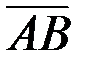 ,
, 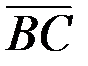 ,
, 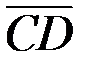 и
и 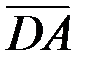 , их длины, записать разложение этих векторов по ортам координатных осей
, их длины, записать разложение этих векторов по ортам координатных осей 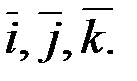
2. Координаты векторов 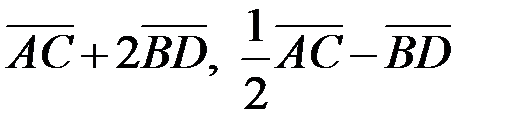 .
.
3. Косинус внутреннего угла АВС.
Задание 2.Даны координаты вершин пирамиды: 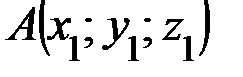 ,
, 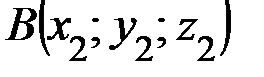 ,
, 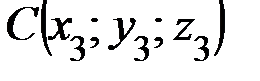 ,
, 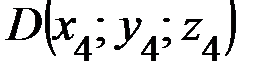 .
.
Найти:
1. Площадь основания АВС пирамиды.
2. Объем пирамиды ABCD.
3. Длину высоты пирамиды DO, опущенную из вершины D на основание АВС.
Задание 3. Даны координаты четырех точек: 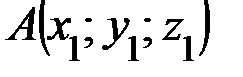 ,
, 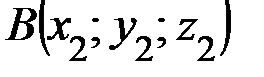 ,
, 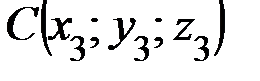 ,
, 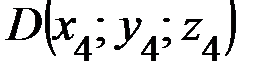 .
.
1. Составить общее уравнение плоскости АВС.
2. Составить канонические и параметрические уравнения прямой АD.
| № варианта | А | В | С | D |
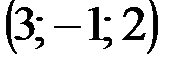 | 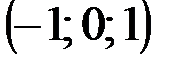 | 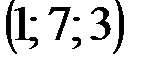 | 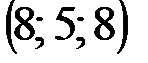 | |
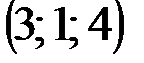 | 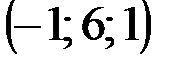 | 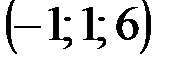 | 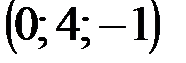 | |
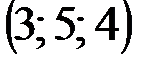 | 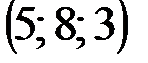 | 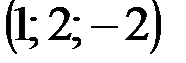 | 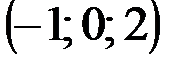 | |
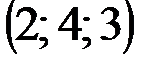 | 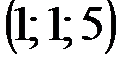 | 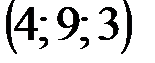 | 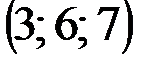 | |
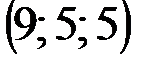 | 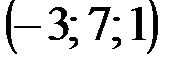 | 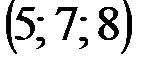 | 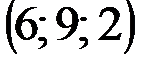 | |
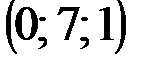 | 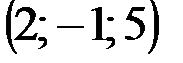 | 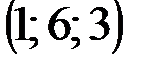 | 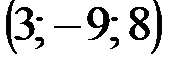 | |
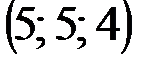 | 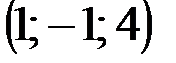 | 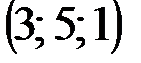 | 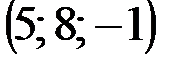 | |
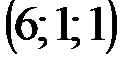 | 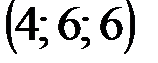 | 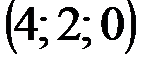 | 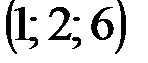 | |
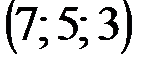 | 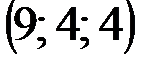 | 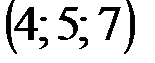 | 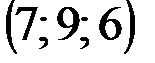 | |
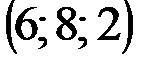 | 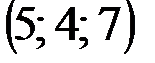 | 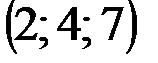 | 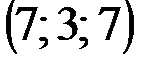 | |
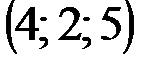 | 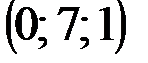 | 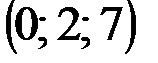 | 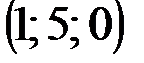 | |
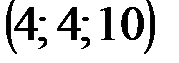 | 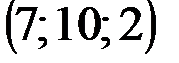 | 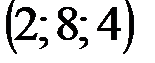 | 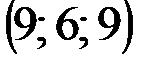 | |
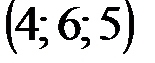 | 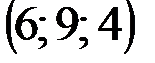 | 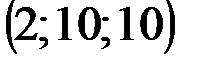 | 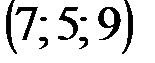 | |
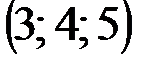 | 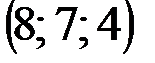 | 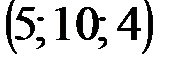 | 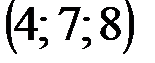 | |
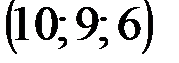 | 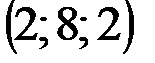 | 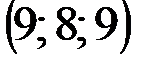 | 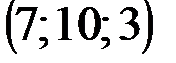 | |
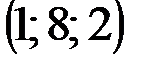 | 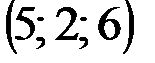 | 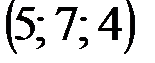 | 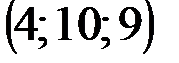 | |
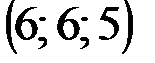 | 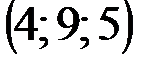 | 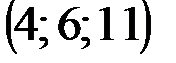 | 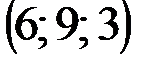 | |
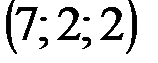 | 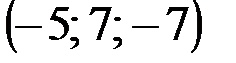 | 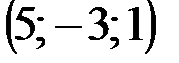 | 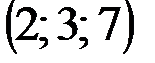 | |
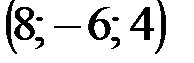 | 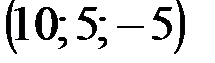 | 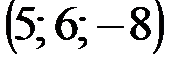 | 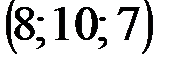 | |
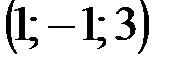 | 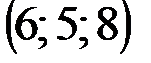 | 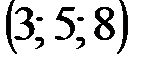 | 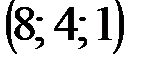 | |
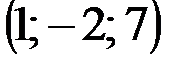 | 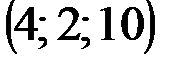 | 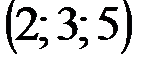 | 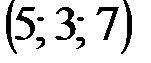 | |
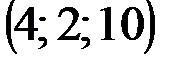 | 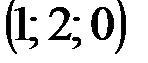 | 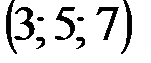 | 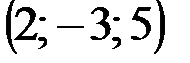 | |
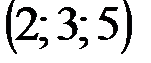 | 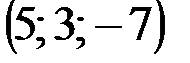 | 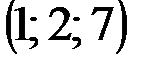 | 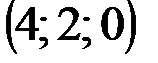 | |
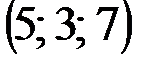 | 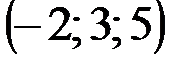 | 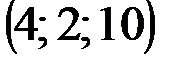 | 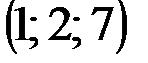 | |
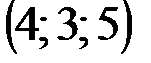 | 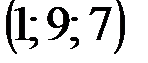 | 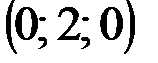 | 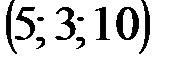 | |
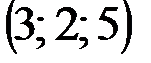 | 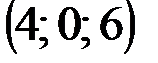 | 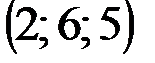 | 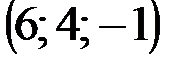 | |
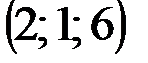 | 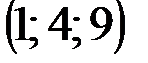 | 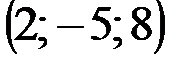 | 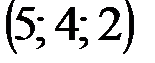 | |
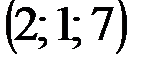 | 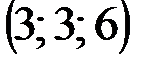 | 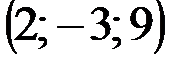 | 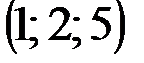 | |
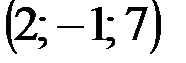 | 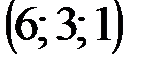 | 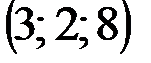 | 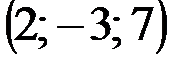 | |
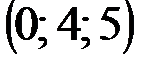 | 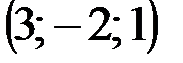 | 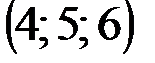 | 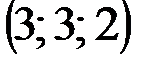 | |
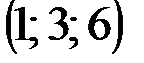 | 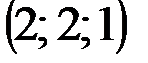 | 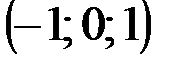 | 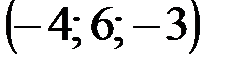 | |
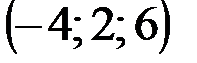 | 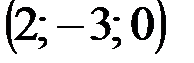 | 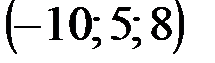 | 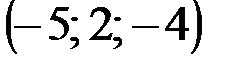 |
Пример(к заданию 1). 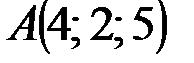 ,
, 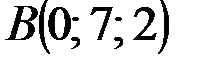 ,
, 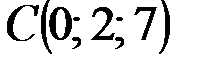 ,
, 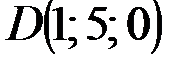 .
.
Решение.
1.Для нахождения координат вектора нужно из координат конца вычесть координаты его начала. Тогда 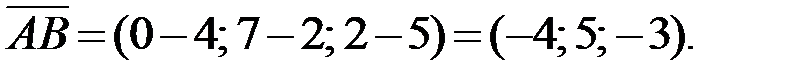 Аналогично находим координаты остальных векторов:
Аналогично находим координаты остальных векторов: 
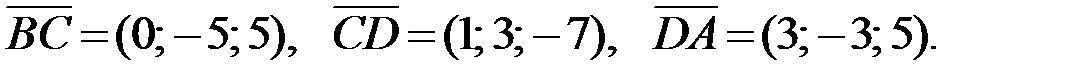
Найдём длины векторов (если 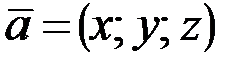 , то
, то 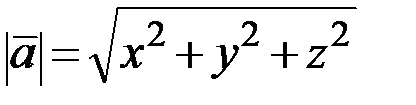 ):
):
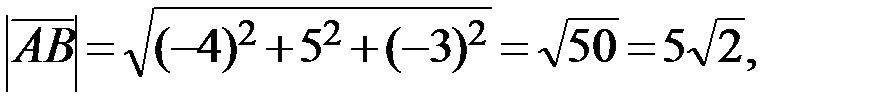
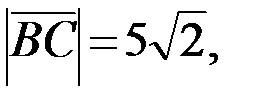
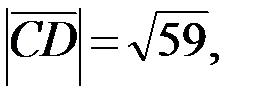
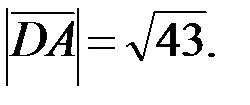
Запишем разложение этих векторов по ортам координатных осей 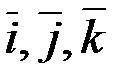 (если
(если 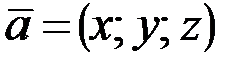 , то
, то 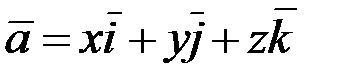 ):
):
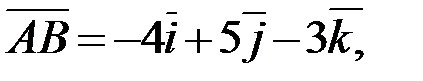
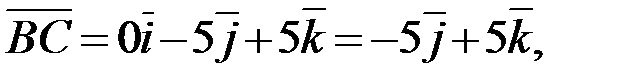
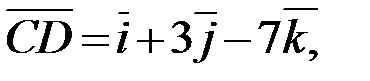
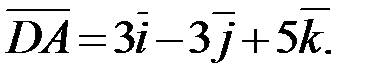
Ответ: 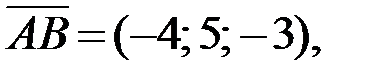
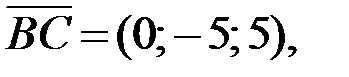
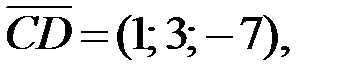
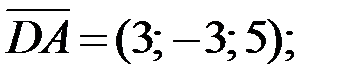
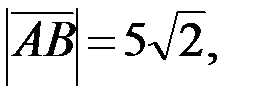
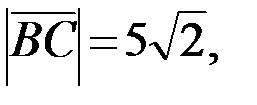
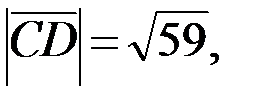
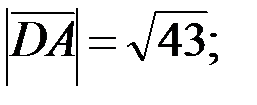
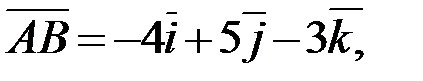
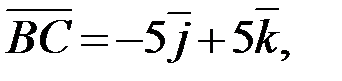
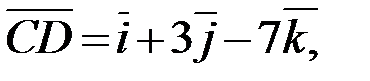
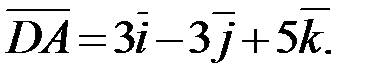
2.Используя правила сложения, вычитания и умножения вектора на число (при сложении векторов складывают соответствующие координаты, при вычитании векторов вычитают соответствующие координаты, при умножении вектора на число каждую координату вектора умножают на это число), получаем:
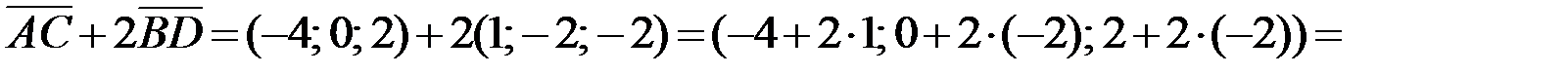
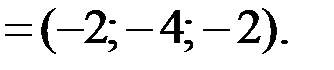
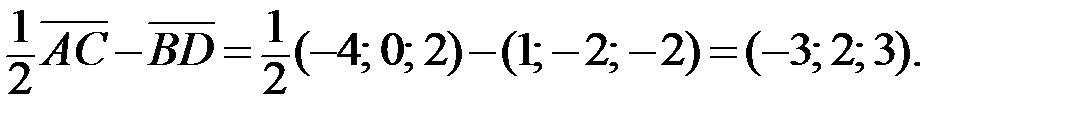
Ответ: 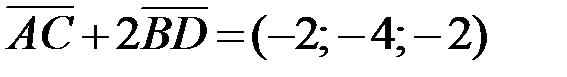 ,
, 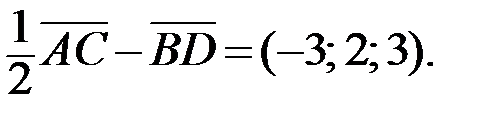
3.Внутренний угол ABC определяется как угол между векторами 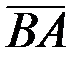 и
и 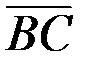 :
: 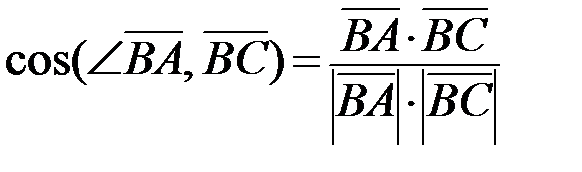 . Найдём координаты этих векторов:
. Найдём координаты этих векторов: 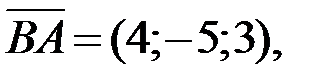
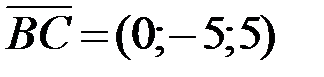 . Далее найдём длины этих векторов:
. Далее найдём длины этих векторов: 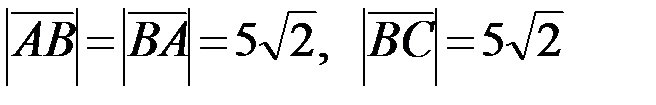 и их скалярное произведение (если
и их скалярное произведение (если 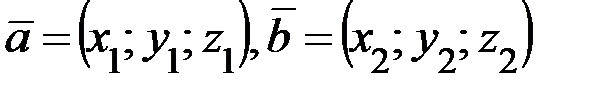 , то
, то 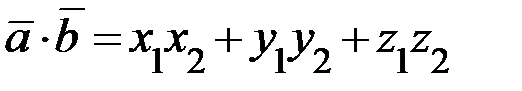 ):
): 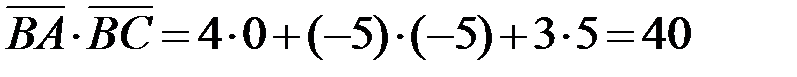 . Тогда косинус внутреннего угла ABC:
. Тогда косинус внутреннего угла ABC:
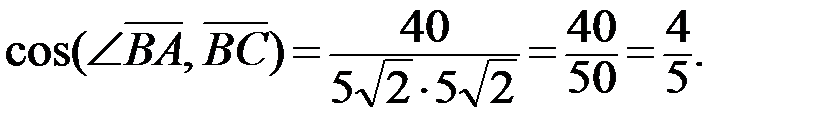
Ответ: 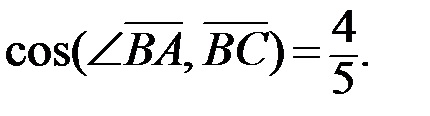
Пример(к заданию 2). 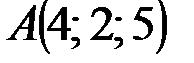 ,
, 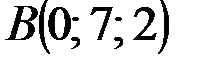 ,
, 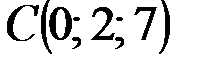 ,
, 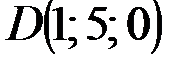 .
.
Решение.
1.Треугольник ABC построен на векторах 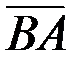 и
и 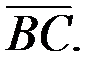 Для вычисления площади основания ABC применяем формулу
Для вычисления площади основания ABC применяем формулу 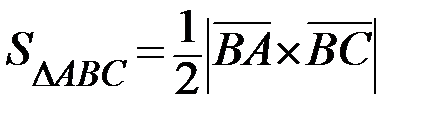 .
.
Найдём векторное произведение векторов 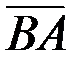 и
и 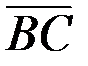 (если
(если 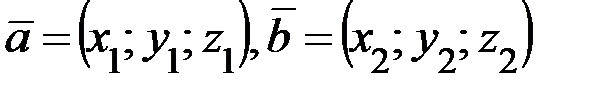 , то
, то 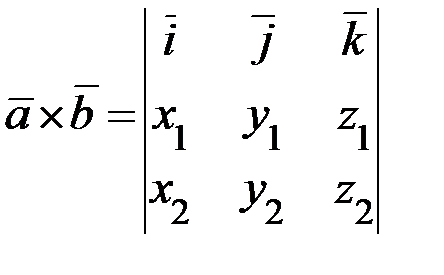 ):
):
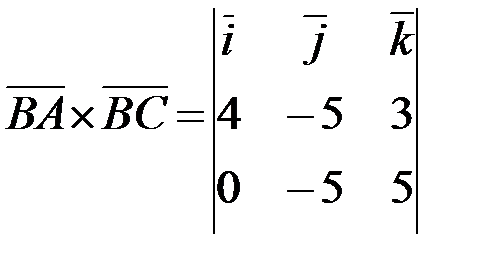 .
.
Раскрываем определитель разложением по первой строке:
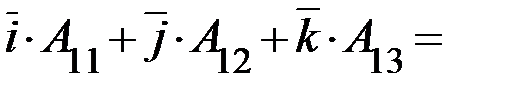
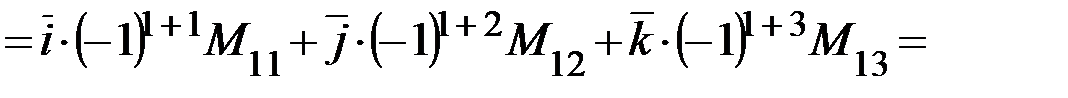
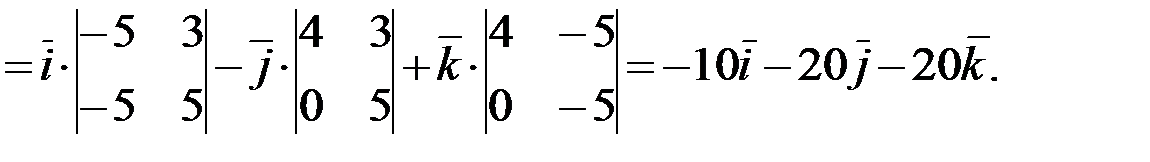
Тогда:
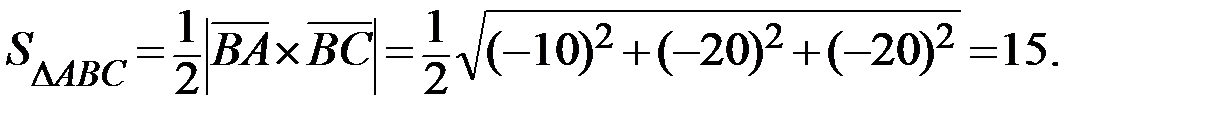
Ответ: 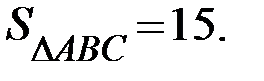
2. Пирамида ABCD построена на векторах 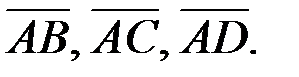 Объём пирамиды ABCD вычисляется как
Объём пирамиды ABCD вычисляется как 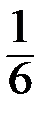 модуля смешанного произведения этих векторов:
модуля смешанного произведения этих векторов: 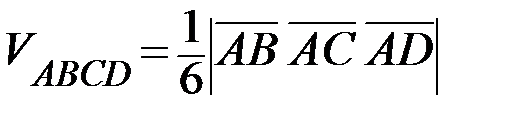 . Так как смешанное произведение векторов равно определителю, составленному из координат этих векторов, то
. Так как смешанное произведение векторов равно определителю, составленному из координат этих векторов, то 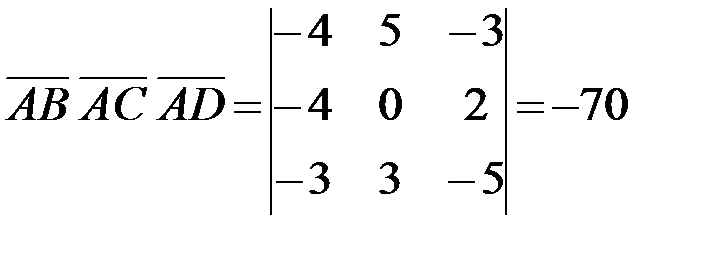 . Тогда
. Тогда 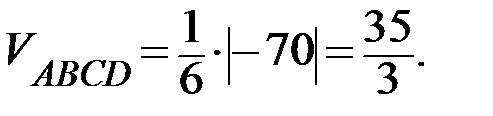
Ответ: 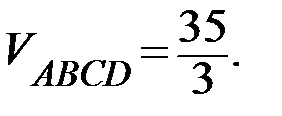
2.Известно, что объём пирамиды равен 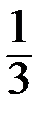 произведения площади основания на высоту:
произведения площади основания на высоту: 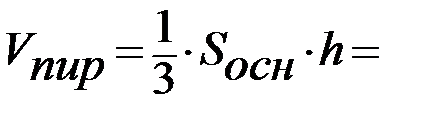
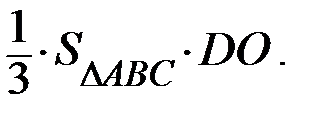 Тогда
Тогда 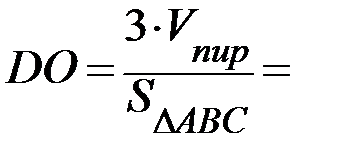
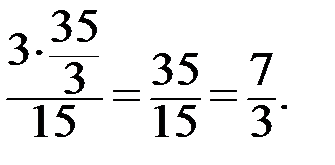
Ответ: 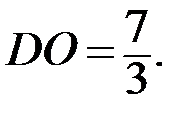
Пример (к заданию 3). 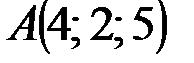 ,
, 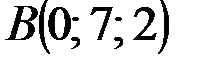 ,
, 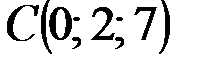 ,
, 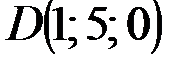 .
.
Решение.
1.Воспользуемся уравнением плоскости, проходящей через три данные точки:
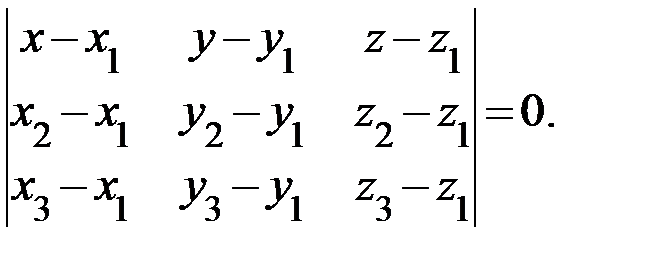
Получаем:
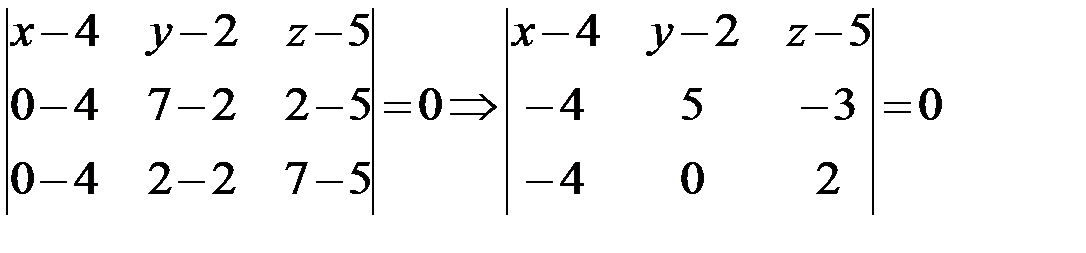 .
.
Раскрываем определитель разложением по первой строке:
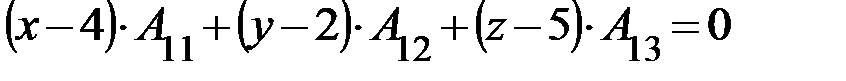
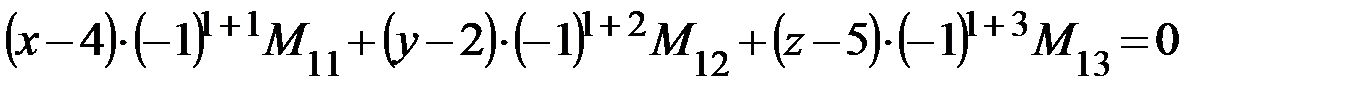
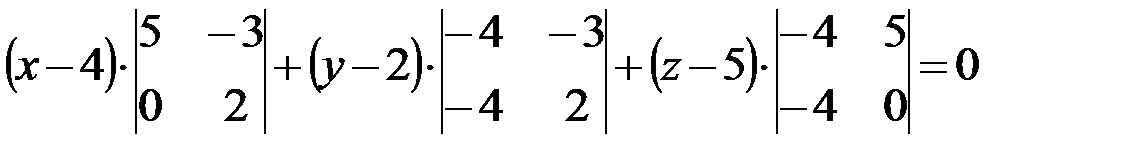
Получаем следующее общее уравнение плоскости:
x+2y+2z–18=0.
Ответ: ABC: x+2y+2z–18=0.
2.Воспользуемся формулами канонических уравнений прямой:
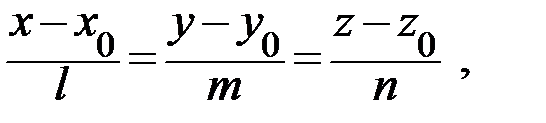
и параметрических
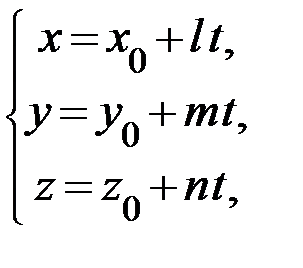
где 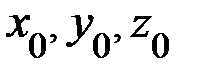 – координаты известной точки прямой, l, m, n – координаты направляющего вектора прямой.
– координаты известной точки прямой, l, m, n – координаты направляющего вектора прямой.
Для составления канонических и параметрических уравнений прямой AD нам понадобится точка, лежащая на этой прямой (можно взять точку A или D), и направляющий вектор этой прямой. В качестве направляющего вектора прямой AD можно взять вектор 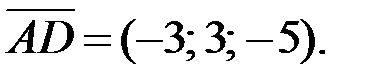 Тогда канонические уравнения прямой AD имеют вид:
Тогда канонические уравнения прямой AD имеют вид:
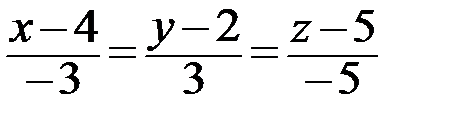
и параметрические уравнения:
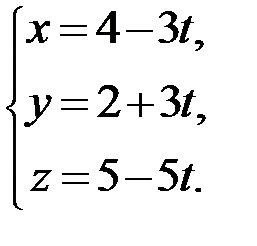
Ответ:
канонические уравнения прямой AD: 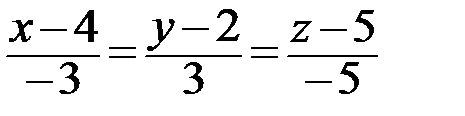 ;
;
параметрические уравнения прямой AD: