ГЛАВА XIII. Аналитическая геометрия.
Аналитическая геометрия на плоскости.
Любая линия на плоскости задается уравнением 
. Для нахождения точек пересечения её с осью Ох надо решить уравнение 
, аналогично с осью Оу: 
. Если какое-либо из уравнений решений не имеет, то точек пересечения с соответствующей осью нет.
Для нахождения точек пересечения двух линий 
и 
необходимо решить систему из уравнений, т.е.
Универсальным способом задания прямой на плоскости является общее уравнение прямой на плоскости: 
, где 
, одновременно не обращаются в ноль. Для описания не вертикальных прямых часто используется уравнение прямой с угловым коэффициентом: 
, 
. Если две прямые заданы уравнениями в этой форме, т.е. 
и 
, то они параллельны, если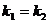 
, и перпендикулярны при 
.
Любое алгебраическое уравнение второй степени относительно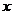 
и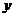 
описывает на плоскости кривую второго порядка.
К основным из них относятся:
1) окружность: 
, 
2) эллипс: 
, 
3) гипербола: 
, или развернутая, когда асимптотами являются оси координат: 
, 
4)парабола: 
или 
, 
.
Аналитическая геометрия в пространстве.
Уравнение прямой, проходящей через точку 
параллельно вектору 
:
.
Уравнение плоскости, проходящей через точку перпендикулярно вектору 
:
Уравнение плоскости, проходящей через три данные точки 
, 
и 
, не лежащие на одной прямой:
Уравнения координатных плоскостей:
плоскость XOY ~ 
; плоскость XOZ ~ 
; плоскость YOZ ~ 
.
ГЛАВА XIV. ТЕОРИЯ ВЕРОЯТНОСТЕЙ.
Случайные события.
Классическое определение вероятности:
Вероятностью события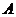 
называется отношения числа благоприятных исходов событию 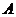к общему числу равновозможных событий, образующих полную группу, т.е.
, при этом очевидно: 
.
События называются несовместными, если наступление одного из них исключает наступление другого.
События называются независимыми, если вероятность наступления одного из них не влияет на вероятность наступления другого.
Теоремы сложения и умножения вероятностей:
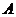– для независимых событий и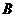 
.
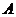– для зависимых событий и .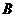
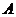– для несовместных событий и .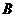
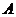– для совместных событий и .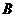
Случайные величины.
Полной характеристикой случайной величины 
является её функция распределения 
. Для дискретной случайной величины более удобной формой задания является ряд распределения:
| |  |  |  |  |
 |  |  | |  |
– возможные значения случайной величины ;
– вероятность того, что случайная величина примет значение 
В ряде задач бывает достаточно иметь не полную информацию о случайной величине, а только её основные числовые характеристики:
– математическое ожидание; 
– дисперсия; 
– среднеквадратическое отклонение.
Формулы для вычисления:
Для непрерывной случайной величины эти характеристики определяются через функцию плотности распределения
; 
Для равномерно распределённой случайной величины функция плотности распределения имеет вид:
Для нормально распределённой случайной величины числовые характеристики являются параметрами плотности распределения:
; 
, 
Для случайной величины распределенной по закону Пуассона:
; 
.
Параметр показательного закона распределения определяется: l=1/ M(X)
Свойства числовых характеристик:
1. 
, 
1. 
,
2. 
2. 
3. 
3. 
независимы