По математике для специальностей инженерно-технического профиля

По математике для специальностей инженерно-технического профиля

Кострома

2002 г

Глава I. Элементы линейной алгебры............................................................... 3

§1.1. Определители.................................................................................................................. 3

§1.2. Матрицы и линейные операции над ними................................................................. 3

Глава II. Векторная алгебра...................................................................................... 4

§2.1 Основные понятия......................................................................................................... 4

§2.2. Операции над векторами.............................................................................................. 4

§ 2.3. Переход к новому базису............................................................................................ 4

ГЛАВА III. КОМПЛЕКСНЫЕ ЧИСЛА................................................................................. 5

§ 3.1. Представление комплексных чисел........................................................................ 5

§ 3.2. Действия над комплексными числами................................................................... 5

ГЛАВА IV. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ.............................................................. 6

ГЛАВА V. ОПЕРАЦИИ МАТЕМАТИЧЕСКОЙ ЛОГИКИ............................................... 6

ГЛАВА VI. КОМБИНАТОРИКА............................................................................................ 6

ГЛАВА VII. ЭЛЕМЕНТАРНАЯ АЛГЕБРА.......................................................................... 7

§ 7.1. Преобразования графиков функций.......................................................................... 7

§ 7.2. Корень уравнения......................................................................................................... 7

ГЛАВА VIII. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ........................................ 7

ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.......................................................................................................................... 8

ГЛАВА X. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ.................................................................... 9

§ 10.1. Неопределенный интеграл........................................................................................ 9

§ 10.2. Определенный интеграл.......................................................................................... 10

§ 10.3. Двойной интеграл..................................................................................................... 10

ГЛАВА XI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ................................................... 10

ГЛАВА XII. ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ.......................................... 11

§ 12.1. Числовые ряды........................................................................................................... 11

§ 12.2. Функциональные ряды............................................................................................ 12

ГЛАВА XIII. Аналитическая геометрия............................................................. 12

§ 13.1. Аналитическая геометрия на плоскости........................................................... 12

§ 13.2. Аналитическая геометрия в пространстве........................................................ 13

ГЛАВА XIV. ТЕОРИЯ ВЕРОЯТНОСТЕЙ.......................................................................... 13

§ 14.1. Случайные события.................................................................................................. 13

§ 14.2. Случайные величины............................................................................................... 13

ГЛАВА XV. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА....................................................... 15

Глава I. Элементы линейной алгебры.

Определители.

Определение: Матрицей называется таблица чисел, в которой m строк и n столбцов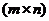

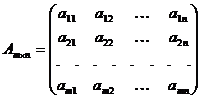, где

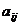– элементы матрицы, 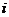– номер строки, 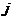– номер столбца

Только для квадратных матриц 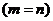введено понятие определителя.

Теорема: Определитель матрицы 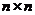или определитель n-го порядка – это число, равное сумме произведений элементов какого-либо столбца (строки) на их алгебраические дополнения. Например для второй строки:

,

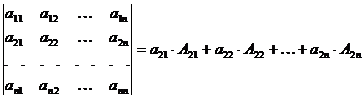где 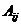– алгебраическое дополнение к элементу ;

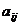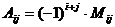
Определение:Минором 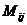элемента 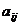называется определитель, получаемый из данного после вычеркивания i-ой строки и j-го столбца.

В частных случаях:

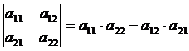
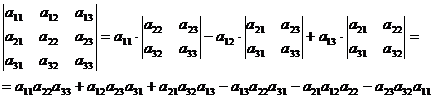
или схематический (метод треугольников):

Матрицы и линейные операции над ними.

, ,

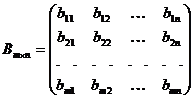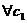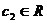, справедливо:

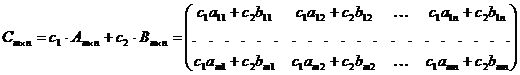
Глава II. Векторная алгебра.

Основные понятия.

Если 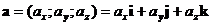, где 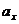; ; 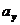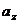– координаты вектора ,

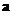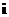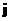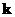, , – вектора базиса; то модуль или длина вектора 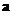определяется по формуле:

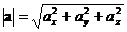
Если вектора 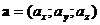и 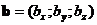коллинеарны, то

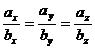
Операции над векторами.

Пусть , .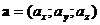

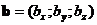Тогда

1)

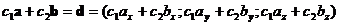
2) Скалярное произведение векторов 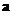и :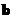

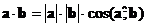
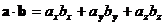
3) В пространстве 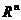последняя формула примет вид: 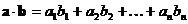, где , .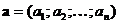

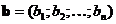Переход к новому базису.

В некотором базисе даны вектора: , , .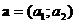

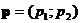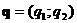Требуется найти координаты вектора 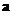в новом базисе, образованном векторам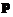и и 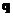, т.е. решить векторное уравнение:

, ,

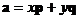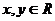которое сводится к системе линейных уравнений:

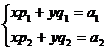
ГЛАВА III. КОМПЛЕКСНЫЕ ЧИСЛА.

Действия над комплексными числами

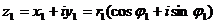
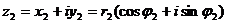
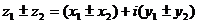
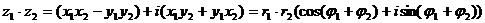
Комплексное число 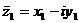называется сопряженным к комплексному числу

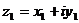
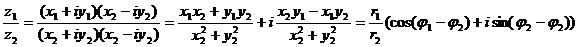
Степени мнимой единицы:

…

…

…

… ,

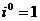
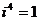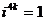
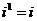
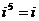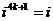
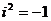
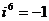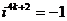
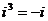
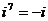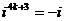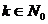
В частных случаях:

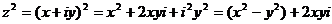
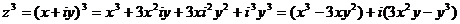
ГЛАВА V. ОПЕРАЦИИ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.

& – знак конъюнкции, логического умножения;

Ú – знак дизъюнкции, логического сложения;

1. , ;

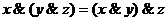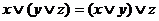2. , ;

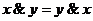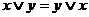3. , ;

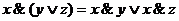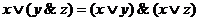4. , ;

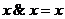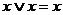5. ;

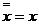6. , , , ;

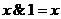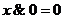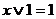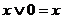7. , ;

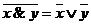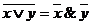8.

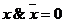
9.

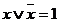
ГЛАВА VI. КОМБИНАТОРИКА.

Сочетания: 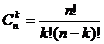(порядок элементов внутри выборки не важен)

Размещения: 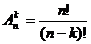(порядок элементов внутри выборки важен)

Перестановки: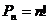

Корень уравнения.

Если уравнение 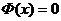имеет единственный корень при 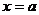, то уравнение 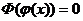так же имеет корень при .

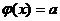Основные неопределенности.

, , , , .

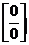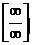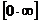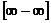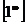Правила дифференцирования.

Если 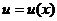, 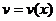– дифференцируемые функции,

то

1.

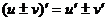
2.

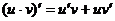
3.

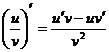
Формулы дифференцирования:

,

,

,

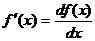
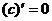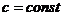
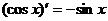
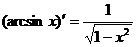
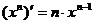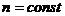
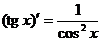
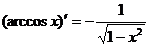
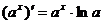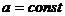
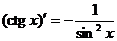
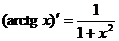
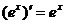
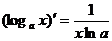
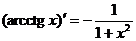
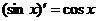
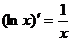
Следствие: ,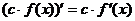

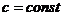
Формула Лапиталя.

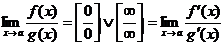
Дифференциал функции.

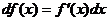
Применение дифференциального исчисления в исследовании функции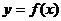

1) Если дифференцируемая функция 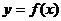возрастает (убывает) на отрезке 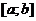, то .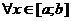

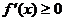
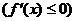2) Если дважды дифференцируемая функция 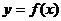выпукла (вогнута) на отрезке 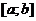, то .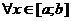

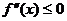
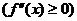Замечание: 1. Частные производные функции нескольких переменных находятся по тем же правилам и формулам, что и для функции одной переменной, полагая, что все переменные, кроме той, по которой производится дифференцирование, являются константами.

2. Градиент функции 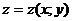определяется по формуле: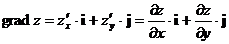

Неопределенный интеграл.

Таблица интегралов.

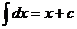
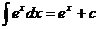
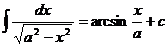
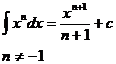
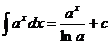
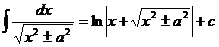
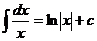
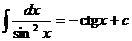
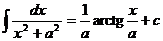
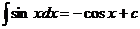
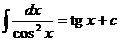
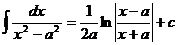
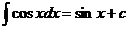
Некоторые тригонометрические формулы, применяемые при интегрировании:

, , ,

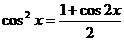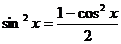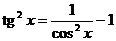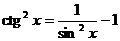
Разложение дроби на простейшие при интегрировании рациональных дробей:

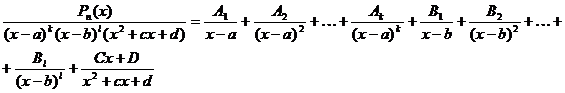
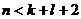, т.е. дробь правильная

Определенный интеграл.

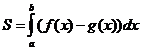
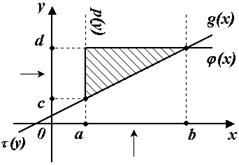
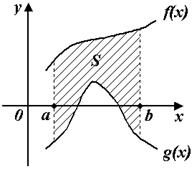§ 10.3. Двойной интеграл.

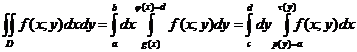
Числовые ряды.

Выражение вида:

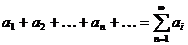, где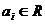

называется числовым рядом. Если 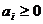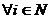, то ряд называется знакопостоянными.

Сумма первых 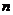членов ряда называется частичной суммой: .

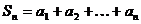Ряд называется сходящимся, если существует 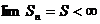, в противном случае – расходящимся. Ряды чаще всего исследуются на сходимость с помощью признаков сходимости.

Для знакопостоянных рядов наиболее применимы следующие:

1. необходимый признак сходимости ряда:

если 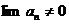, то ряд расходится, при 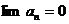– ответ дать нельзя;

2. признак Даламбера:

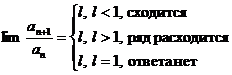
3. признаки сравнения;

4. признак Коши: Если 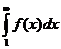сходится, то и ряд сходится; если интеграл расходится, то и ряд расходится. Функция 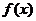строится по формуле 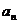– общего члена ряда:

, , … , , …

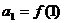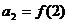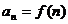Замечание: 1. Ряд вида 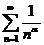называется гармоническим. При 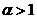ряд сходится, при 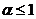– расходится.

2. Ряд, составленный из членов геометрической прогрессии 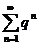сходится при 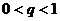, и расходится, если .

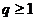Функциональные ряды.

Ряд Тейлора для функции :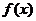

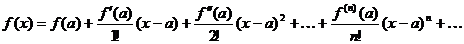
Случайные события.

Классическое определение вероятности:

Вероятностью события 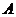называется отношения числа благоприятных исходов событию 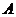к общему числу равновозможных событий, образующих полную группу, т.е.

, при этом очевидно: .

События называются несовместными, если наступление одного из них исключает наступление другого.

События называются независимыми, если вероятность наступления одного из них не влияет на вероятность наступления другого.

Теоремы сложения и умножения вероятностей:

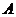– для независимых событий и .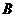

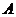– для зависимых событий и .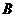

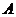– для несовместных событий и .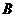

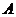– для совместных событий и .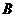

Случайные величины.

Полной характеристикой случайной величины является её функция распределения . Для дискретной случайной величины более удобной формой задания является ряд распределения:

– возможные значения случайной величины ;

– вероятность того, что случайная величина примет значение

В ряде задач бывает достаточно иметь не полную информацию о случайной величине, а только её основные числовые характеристики:

– математическое ожидание; – дисперсия; – среднеквадратическое отклонение.

Формулы для вычисления:

Для непрерывной случайной величины эти характеристики определяются через функцию плотности распределения

;

Для равномерно распределённой случайной величины функция плотности распределения имеет вид:

Для нормально распределённой случайной величины числовые характеристики являются параметрами плотности распределения:

; ,

Для случайной величины распределенной по закону Пуассона:

; .

Параметр показательного закона распределения определяется: l=1/ M(X)

Свойства числовых характеристик:

1. , 1. ,

2. 2.

3. 3.

независимы

по математике для специальностей инженерно-технического профиля

Кострома

2002 г

Глава I. Элементы линейной алгебры............................................................... 3

§1.1. Определители.................................................................................................................. 3

§1.2. Матрицы и линейные операции над ними................................................................. 3

Глава II. Векторная алгебра...................................................................................... 4

§2.1 Основные понятия......................................................................................................... 4

§2.2. Операции над векторами.............................................................................................. 4

§ 2.3. Переход к новому базису............................................................................................ 4

ГЛАВА III. КОМПЛЕКСНЫЕ ЧИСЛА................................................................................. 5

§ 3.1. Представление комплексных чисел........................................................................ 5

§ 3.2. Действия над комплексными числами................................................................... 5

ГЛАВА IV. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ.............................................................. 6

ГЛАВА V. ОПЕРАЦИИ МАТЕМАТИЧЕСКОЙ ЛОГИКИ............................................... 6

ГЛАВА VI. КОМБИНАТОРИКА............................................................................................ 6

ГЛАВА VII. ЭЛЕМЕНТАРНАЯ АЛГЕБРА.......................................................................... 7

§ 7.1. Преобразования графиков функций.......................................................................... 7

§ 7.2. Корень уравнения......................................................................................................... 7

ГЛАВА VIII. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ........................................ 7

ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.......................................................................................................................... 8

ГЛАВА X. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ.................................................................... 9

§ 10.1. Неопределенный интеграл........................................................................................ 9

§ 10.2. Определенный интеграл.......................................................................................... 10

§ 10.3. Двойной интеграл..................................................................................................... 10

ГЛАВА XI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ................................................... 10

ГЛАВА XII. ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ.......................................... 11

§ 12.1. Числовые ряды........................................................................................................... 11

§ 12.2. Функциональные ряды............................................................................................ 12

ГЛАВА XIII. Аналитическая геометрия............................................................. 12

§ 13.1. Аналитическая геометрия на плоскости........................................................... 12

§ 13.2. Аналитическая геометрия в пространстве........................................................ 13

ГЛАВА XIV. ТЕОРИЯ ВЕРОЯТНОСТЕЙ.......................................................................... 13

§ 14.1. Случайные события.................................................................................................. 13

§ 14.2. Случайные величины............................................................................................... 13

ГЛАВА XV. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА....................................................... 15