Алгебра кос (можно как расширение к вопросу36)

Косы - один из простейших геометрических объектов, легко поддающийся «алгебраизации»: косы с одинаковым числом нитей можно умножать. Делается это совсем просто (см. рис. 4): нужно приложить одну косу к другой, склеив соответствующие нити, и удалить ставшие ненужными гвоздики (нижние гвозди первой косы верхние – второй).

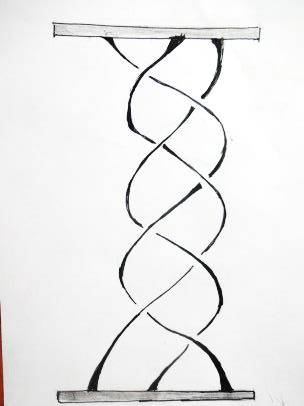К	L	M = K × L
Рис. 4. Умножение кос

Такое умножениеобладает рядом свойств обычного умножения чисел: выполняется ассоциативный закон

К₁(К₂К₃)=(К₁К₂)К_3,

есть аналог единицы – тривиальная коса К₂ = 1, для которой

.

Умножение кос не коммутативно.
Есть и аналог деления:у каждой косы К имеется обратная коса : для нее

.

Рассмотрим данную операцию на рисунке 5.

К	К-1	К × К-1 = 1

Проблему классификации кос можно решать с помощью

основных соотношений теории кос:

Тривиальные соотношения

SjSj- 1 = Sj-1S j = 1 , Sj.1=1 .Sj=S j(j=1, 2,…, n-1).

Соотношения далекой коммутативности

SiS j =SjSiпри i-j 2 (i,j=1,2,…, n-1).

3. Соотношения сплетения SiSi+1SiSi+1 (i=1, 2, …, n-2).

Доказательство.

Любая коса представляется в виде произведения элементарных кос S1,S2,…,Sn-1и обратных к ним,например,

K1=S1S2-1S1S2-1S1S2-1., K3=S2S1S3-1S1-1S3S2-1S1S3S1-1S3-1.

Узел - замкнутая кривая без самопересечения,узел можно описать двумерной диаграммой.

Конечный набор замкнутых непересекающихся ориентированных ломаных в прост­ранстве называетсязацеплением.

Два узла называются эквивалентными, если узел, сжимая, растягивая, двигая в пространстве (без разрывов и склеек), можно превратить в другой.

Главной проблемой теории узлов является поиск инварианта, препятствующего распутыванию.

Теорема.

Любой узел является замыканием некоторой косы.

Возьмём косу, изогнём её дугой и склеим конец с началом, получится узел. Но замыкание разных кос не всегда приводит - к разным узлам. Например, коса из трёх нитей не совпадает с косой из двух нитей, но при замыкании тоже даёт узел "трилистник"(рис.3).

рис.3

рис.4.

Теорема Рейдемейстера

Два узла эквивалентны тогда и только тогда, когда от диаграммы одного узла к диаграмме другого можно перейти с помощью конечного числа двумерных элементарных операций 1, 2, 3 (рис.4).

Можно ли по любой паре диаграмм узнать, эквивалентны узлы или нет, можно ли их распутать?

Оказывается можно, для каждого узла и зацепления можно построить соответствующий ему инвариант. Инварианты позволяют не только различать неодинаковые узлы и отличать узлы от незаузленных петель, но и классифицировать косы. По-разному деформированным вариантам одного и того же узла отвечает один и тот же инвариант; узлы, соответствующие разным инвариантам различны. Но два узла с одним и тем же инвариантом необязательно эквивалентны. Если инвариант узла не равен инварианту тривиального узла, то данный узел не может быть тривиальным и его нельзя распутать. Рассмотрим самые известные инварианты и вычислим их для некоторых зацеплений.

Многочлен Александера.

Этот многочлен был открыт американским математиком Александером в 1928 году. Он строится в соответствии с числом пересечений каждого вида, имеющихся на диаграмме узла. Например, узлу «трилистник» соответствует многочлен Δ_K(t)=t–1–1/t.

Многочлен Конвея

Р_L (х) - это многочлен от переменной х с целыми коэффициентами.

Теорема.

Для каждого узла или зацепления Lполином РL(х) существует и однозначно определяет­ся следующими тремя аксиомами.

Аксиома 1.

Эквивалентным диаграммам L и L’ отвечает один и тот же полином: РL(х)=РL’(х).

Аксиома 2.

Тривиальному узлу отвечает по­лином, равный 1:Ро(х)==1.

Аксиома 3.

Трем зацеплениям L⁺, L-, L°, которые всюду одинаковы, кроме кружочка, где они выгля­дят так, как показано на рисунке 5, отвечают полиномы, связанные соот­ношением

РL+(х)-РL-(х)=х.РL0(х).

рис.5

Теорема.

Для распавшегося зацепления Р_L (х) =О.

Вычислим полиномы Конвея для некоторых узлов и зацеплений.

а) Для двух незацепленных окружностей.

L+- диаграмма тривиального узла с одной двой­ной точкой, L°- диаграмма двух незацепленных окруж­ностей. Из аксиом I и II следует, что РL+(х) = 1.

Если заменить двойную точку диаграммы L+на противоположную, а затем двойную точку уничтожить (аксиома III), то мы полу­чим диаграмму тривиального узла L-и пару незацепленных окруж­ностей L°.

По аксиоме III, получим РL+(х)-РL-(х)=х.РL0(х),1—1=х.РL0(х),РL0(х)=0.

б) Для двух зацепленных окружностей (правое зацепление):

Применяя аксиому III к правой двойной точке, получаем диаграмму L-, эквивалентную паре незацепленных окружностей, и тривиальный узел (с одной двойной точкой) L°.

Используя аксиому I и предыдущий подсчет, получаем РL-(х)=0.

Затем по аксиомам I и II получаем РL0(х)=1.

Подставляя эти значения в соотноше­ние аксиомы III, получим РL+(х)=х.Для левого зацепления полином равен –х

в) Для узла «трилистник»

Р_L(х)=1,т.к. распутывается в тривиальный узел.
Р_L⁰(х) =- х, т.к. распутывается в левое зацепление двух окружностей, значит, Р_L (х) = 1 - х² по аксиоме 3.

г) Для восьмерки.

Р_L (х) = х, так как распутывается в правое зацепление двух окружностей.
Р_L (х) = 1, так как распутывается в тривиальный узел.

Поэтому P_L’ (x) = 2х по аксиоме 3.

д) Для проколотой восьмеркиР_L (х) = х, так как распутывается в правое зацепление двух окружностей.

Пусть зацепление L1 = L⁰.Тогда Р_L1(х)= 1. Р_L1⁰(х) = х, так как распутывается в правостороннее зацепление двух окружностей.

Значит, Р_L1 (х) = х² + 1. В итоге Р_L (х) = х³+ 2х .

Даже небольшое число проведенных вычислений показывает, что полином Конвея — достаточно тонкий инстру­мент, позволяющий различать узлы и зацепления и устанавливать их нетри­виальность. Посчитав, например, по­линомы трилистника, восьмерки, и убедившись, что эти полиномы не равны 0 или 1, мы доказали, что их нельзя распу­тать. Разумеется, эти доказательства верны только в том случае, если уже установлен факт существования и единственности полинома Конвея для каждого узла и зацепления.