Вопрос 19 Геометрические фракталы: триадная кривая Кох.

Геометрические фракталы самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

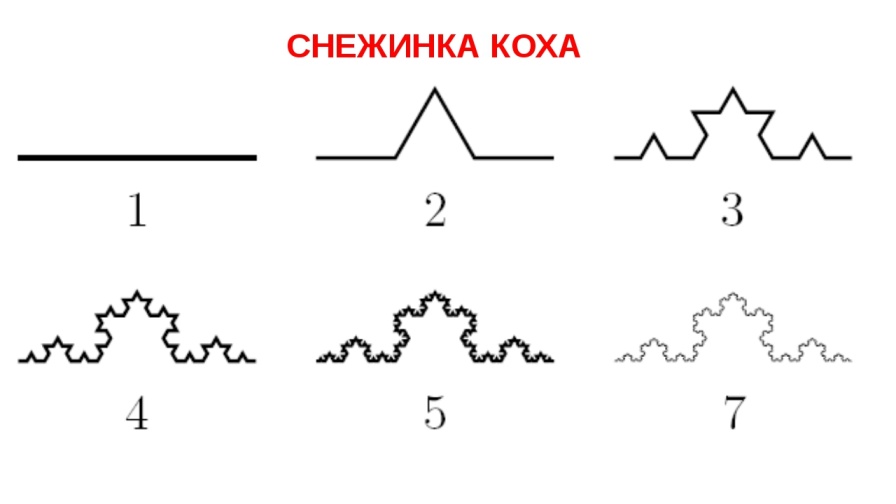
Рассмотрим один из таких фрактальных объектов - триадную кривую Коха. Построение кривой начинается с отрезка единичной длины (рис. 1.6) - это 0-е поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.1 через n=1. В результате такой замены получается следующее поколение кривой Кох. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия - каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n-го поколения при любом конечном n называется предфракталом. На рис. 1.6 представлены пять поколений кривой. При n стремящемся к бесконечности кривая Кох становится фрактальным объектом.

Геометрические фракталы: салфетка Серпинского.

Рассмотрим самоподобную фигуру, придуманную польским математиком В.Серпинским (1882–1969).

Она получается из квадрата последовательным вырезанием серединных квадратов. Проследим построения нового квартала более подробно. Разделим данный квадрат на девять равных квадратов и квадрат, расположенный в середине, вырежем. Получим квадрат с пустотой (рис. 10а). Для оставшихся восьми квадратов вновь повторим указанную процедуру. Разделим каждый из них на девять равных квадратов и серединные квадраты удалим (рис. 10б). Повторяя похожие построения, будем получать все более “дырявую” фигуру (рис. 10в). То, что остается после всех вырезаний, и будет ковром Серпинского.

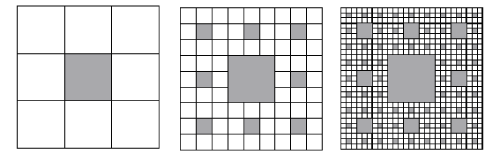
а) б) в)

Рис. 10

Поскольку вырезаемые квадраты располагаются все более часто, то в результате на ковре (салфетке) Серпинского не будет ни одного, даже самого маленького, квадрата без «дырки».

Начиная не с квадрата, а с равностороннего треугольника, и вырезая центральные треугольники, получим еще одну самоподобную фигуру, аналогичную ковру Серпинского. Она носит название «салфетки Серпинского» (рис. 11).

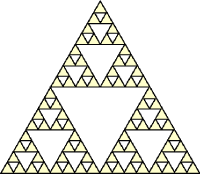
Рис. 11

Фрактал Кантора.

Георг Кантор (1845-1918) явился одним из основателей теории множеств. Он также придумал один из старейших фракталов - множество Кантора (описано им в 1883) (называют иногда пылью). Фрактальные свойства пыли Кантора имеют огромное значение, особенно учитывая тот факт, что многие известные фракталы являются близкими родственниками этого фрактала.

Кантор с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая Пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками.

Способ построения этого множества следующий. Берётся отрезок прямой единичной длины. Затем он делится на три равные части, и вынимается средний отрезок. Это первый шаг итерационной процедуры. На втором шаге подобной процедуре деления на три равные части и последующего удаления середины подвергается каждый из двух оставшихся отрезков. Так продолжая до бесконечности, получим множество Кантора. Нетрудно заметить, что суммарная длина получившихся в пределе отрезков равна нулю, так кам мы исключили в результате длину, равную 1:

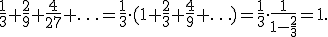
Проведём построение более формально на множестве. Берём отрезок единичной длины 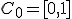. Удаляем из него открытый интервал 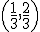, получая 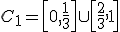. На следующем и всех остальных шагах вы выкидываем среднюю треть (не включая концы) всех отрезков текущего уровня. Т. о. на втором шаге мы имеем 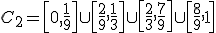. Предельное множество 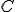, которое представляет собой пересечение множеств 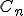, , 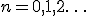и представляет собой пыль Кантора.

Множество Кантора имеет мощность континуума. Для этого необходимо установить взаимно однозначное соответствие между точками из множества Кантора и точками отрезка 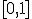. Будем представлять все точки отрезка 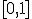в виде двоичной дроби, а точки пыли Кантора в виде троичной дроби. В случае, когда точка имеет два представления, мы будем всегда выбирать то, которое заканчивается всеми единицами в двоичном виде и всеми двойками в троичном. Заметим, что точка попадает в множество Кантора тогда и только тогда, когда в ее троичном представлении присутствуют только нули и двойки, поэтому искомое соответствие осуществляется заменой всех двоек в троичном представлении на единицы. Описанная процедура и определяет ваимно однозначное соответствие между множеством Кантора и отрезком .

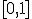Непосредственно с множеством Кантора связана чёртова лестница.

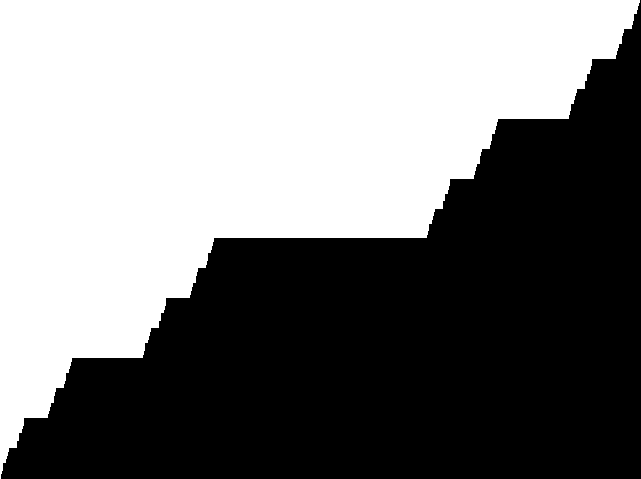
Фрактальная размерность. Примеры вычисления размерности фракталов.

Фрактал – множество с дробной размерностью.

Фрактал – множество, размерность Хайсдорфа-Безиковича которого строго больше топологической размерности.

Типы размерности:

1) Евклидова: минимальное число координат, необходимых для однозначного определения положения точки;

2) Тополог.: размерность любого множества на 1 больше размерности разреза, делящего его на две несвязнае части (тополог.размерность отрезка-1, топол.разм. квадрата-2, плоскости-2);

3) Размерность самоподобия 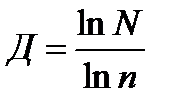. Размерность самоподобия – один из частных случаев фрактальной размерности.

Размерность Хаусдорфа — естественный способ определить размерность подмножества в метрическом пространстве.

Размерность Хаусдорфа согласуется с нашими обычными представлениями о размерности в тех случаях, когда эти обычные представления есть. Например, в трёхмерном евклидовом пространстве хаусдорфова размерность конечного множества равна нулю, размерность гладкой кривой — единице, размерность гладкой поверхности — двум и размерность множества ненулевого объёма — трём. Для более сложных (фрактальных) множеств размерность Хаусдорфа может не быть целым числом.