Современное состояние математики как науки. Математика в системе наук

Современное состояние математики как науки. Математика в системе наук

Математика – это наука о количественных отношениях и пространственных формах действительного мира (Ф.Энгельс, придерживаемся определения до этого времени). В нее входят такие дисциплины, как арифметика, алгебра, геометрия, тригонометрия, высшая математика (аналитическая геометрия, линейная алгебра, математический анализ, дифференциальное и интегральное исчисления и др.). Каждая из них изучает количественные отношения и пространственные формы мира в особом аспекте и действует своими собственными методами.

Период современной математики (XIX – начало XXI вв.) характеризуется следующими основными чертами:

Углубленный анализ накопленного математикой огромного фактического материала и объединение его с новых точек зрения.

Активная разработка проблем обоснования математики: критический пересмотр ее исходных положений (аксиом), построение строгой системы определений и доказательств, критический анализ логических приемов, употребляемых в ходе этих доказательств.

Расширение круга количественных отношений и пространственных форм, изучаемых математикой: исследуются отношения между элементами произвольной группы, векторами, операторами в функциональных пространствах, все разнообразие форм пространств любого числа измерений и т.п.

Сознательное и активное создание математиками принципиально новых математических теорий на основе аксиоматического метода путем правильно выполненного абстрагирования от налагавшихся ранее ограничений, не имеющих внутренней логической необходимости. Наиболее яркие примеры – создание неевклидовых геометрий и многомерных алгебр.

Формирование новых математических дисциплин, таких как дискретная математика, математическая логика, теория алгоритмов, теория информации, теория игр, математическое программирование и др.

Усложнение и углубление традиционных связей с естествознанием и техникой, расширение использования математических методов в биологии, социальных и гуманитарных науках.

Расширение области применения математики вследствие развития ЭВМ и компьютеризации всех сфер общественной жизни.

Математика — это фундаментальная наука, методы которой, активно применяются во многих сферах деятельности.

(((Известный датский физик Нильс Бор говорил, что математика является значительно большим, чем наука – она является языком науки. И, наверное, поэтому до настоящего времени среди философов нет единого мнения о том, является ли математика наукой в общепринятом смысле. Наука — область человеческой деятельности, направленная на выработку и систематизацию объективных знаний о действительности. Основой этой деятельности является сбор фактов, их постоянное обновление и систематизация, критический анализ и, на этой основе, синтез новых знаний или обобщений, которые не только описывают наблюдаемые природные или общественные явления, но и позволяют построить причинно-следственные связи с конечной целью прогнозирования.)))

Потребности науки и техники стимулируют развитие теоретической математики. Так, создание метода наименьших квадратов связано с геодезическими работами; из запросов электротехники возник новый раздел теории вероятностей – теория информации; развитие методов приближенного решения дифференциальных уравнений связано с нуждами астрономии и т.д.

Приложения математики весьма разнообразны. Принципиально область применения математического метода не ограничена: все формы движения материи, а также сознание могут исследоваться математически.

В настоящее время наиболее универсальными математическими методами, широко и успешно применяемыми в разных науках, являются методы математической гипотезы и математического моделирования. Данные методы позволяют спрогнозировать и изучать явления в любой сфере человеческой деятельности, поэтому они используются не только в естествознании, но также и в социально-гуманитарных науках.

Характерные черты математики как науки. Противоречия как движущие силы математики. Источники нового в математике: практика, внутренние потребности самой математики, необходимость обоснования математики.

Отметим следующие характерные черты математической науки:

1) Математика изучает абстрагированные свойства предметов — числа, а не совокупности предметов, геометрические фигуры, а не реальные тела. При этом математика абсолютизирует свои абстракции: возникшие в ходе ее развития математические понятия в дальнейшем закрепляются и рассматриваются как данные. Например, хотя теперь известно, что свойства реального пространства отличны от предполагавшихся Евклидом, построенная им геометрия сохранила свое значение, как одна из возможных моделей реального пространства. Сравнение результатов, полученных в математике, с реальной действительностью является задачей не столько математики, сколько ее приложений.

2) Основным методом получения математических результатов является логический вывод, не опирающийся на экспериментальную проверку.

3) Как следствие этого имеет место непреложность математических выводов. Если приняты исходные посылки, то полученные из них математическим путем результаты непреложны. Если же результаты расходятся с опытом, то следует подвергнуть исследованию принятые посылки.

4) Абстракции, возникающие в математике, развиваются ступенчато — от абстракций, непосредственно обобщающих свойства реальных предметов, к абстракциям столь высокого уровня, как топологические пространства, общие алгебраические системы, алгоритмы и т. д.

5) Математика обладает свойством универсальной применимости. В любой области, где только удается математически поставить задачу, математика дает результат с точностью, соответствующей точности постановки задачи. При этом, чем более отвлеченными от содержания являются используемые в исследовании понятия и методы, тем шире область возможных применений этих методов. Однако эта универсальность не является абсолютной — сама возможность применения математических методов предполагает известный уровень абстрактности данной науки. Кроме того, ошибочность принятых положений не может быть исправлена сколь угодно тонким математическим анализом.

6) Наконец отметим, что математика занимает особое положение в системе наук — её нельзя отнести ни к гуманитарным, ни к естественным наукам. Она дает те основные понятия, которые используются почти во всех науках. Такие понятия, как «множество», «структура», «система», «изоморфизм» и т. д., впервые возникшие в математике, сейчас приобрели статус общенаучных понятий.

Практика является одним из важных источников новых проблем и понятий в математике. Однако прогресс математики невозможен без внутреннего развития самой математики. Стремление к общности результатов, их завершенности независимо от возможных применений — неисчерпаемые источники прогресса математики. На всех этапах ее развития постоянно возникали и возникают проблемы, связанные с упорядочением и переосмысливанием, полученных ранее результатов. Так, упорядочение логических основ математики привело к созданию н развитию таких ее абстрактных областей, как математическая логика, теория алгоритмов, теория множеств. Примером внутреннего развития математической теории может служить также теория случайных процессов, возникшая в 30-х годах нашего столетия из разрозненных фактов и примеров физики, демографии, радиотехники.

Наконец, существует еще немаловажный стимул в развитии математики — любопытство и воображение исследователя. Стремление к познанию окружающего нас мира является характерной чертой человека, это движущая сила прогресса всего человеческого общества. При этом здравый смысл и интуиция играют важную роль в творчестве математиков. Более того, ряд выдающихся математических идей появились, опередив существующие стандарты строгости. Так было, например, с созданием основ анализа бесконечно малых величин, а также с такими фундаментальными понятиями математики, как предел, алгоритм, вероятность, которыми пользовались без строгого их уточнения. Вместе с тем, какой бы полезной ни была математическая идея, рано или поздно возникает необходимость в построении строгого логического фундамента, обеспечивающего формальную непротиворечивость математической теории.

Потребности развития самой математики, "математизация" различных областей науки, проникновение математических методов во многие сферы практической деятельности, прогресс вычислительной техники привели к появлению ряда новых математических дисциплин, например, исследование операций, теория игр, математическая экономика и др.

В основе построения математической теории лежит аксиоматический метод, при котором в фундамент теории кладутся некоторые исходные положения, называемые аксиомами теории, а все остальные предложения теории получаются как логические следствия аксиом. Примером применения аксиоматического подхода в математике является евклидовая геометрия, в которой четко проведена идея получения основного содержания геометрической теории чисто дедуктивным путем из небольшого числа аксиом, истинность которых представлялась наглядно очевидной.

Фрактал Кантора.

Георг Кантор (1845-1918) явился одним из основателей теории множеств. Он также придумал один из старейших фракталов - множество Кантора (описано им в 1883) (называют иногда пылью). Фрактальные свойства пыли Кантора имеют огромное значение, особенно учитывая тот факт, что многие известные фракталы являются близкими родственниками этого фрактала.

Кантор с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая Пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками.

Способ построения этого множества следующий. Берётся отрезок прямой единичной длины. Затем он делится на три равные части, и вынимается средний отрезок. Это первый шаг итерационной процедуры. На втором шаге подобной процедуре деления на три равные части и последующего удаления середины подвергается каждый из двух оставшихся отрезков. Так продолжая до бесконечности, получим множество Кантора. Нетрудно заметить, что суммарная длина получившихся в пределе отрезков равна нулю, так кам мы исключили в результате длину, равную 1:

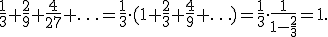
Проведём построение более формально на множестве. Берём отрезок единичной длины 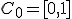. Удаляем из него открытый интервал 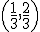, получая 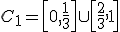. На следующем и всех остальных шагах вы выкидываем среднюю треть (не включая концы) всех отрезков текущего уровня. Т. о. на втором шаге мы имеем 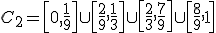. Предельное множество 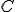, которое представляет собой пересечение множеств 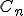, , 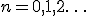и представляет собой пыль Кантора.

Множество Кантора имеет мощность континуума. Для этого необходимо установить взаимно однозначное соответствие между точками из множества Кантора и точками отрезка 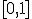. Будем представлять все точки отрезка 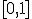в виде двоичной дроби, а точки пыли Кантора в виде троичной дроби. В случае, когда точка имеет два представления, мы будем всегда выбирать то, которое заканчивается всеми единицами в двоичном виде и всеми двойками в троичном. Заметим, что точка попадает в множество Кантора тогда и только тогда, когда в ее троичном представлении присутствуют только нули и двойки, поэтому искомое соответствие осуществляется заменой всех двоек в троичном представлении на единицы. Описанная процедура и определяет ваимно однозначное соответствие между множеством Кантора и отрезком .

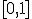Непосредственно с множеством Кантора связана чёртова лестница.

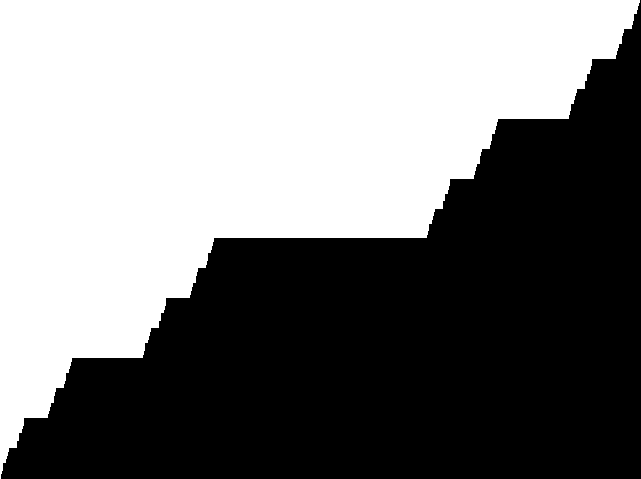
Фрактальная размерность. Примеры вычисления размерности фракталов.

Фрактал – множество с дробной размерностью.

Фрактал – множество, размерность Хайсдорфа-Безиковича которого строго больше топологической размерности.

Типы размерности:

1) Евклидова: минимальное число координат, необходимых для однозначного определения положения точки;

2) Тополог.: размерность любого множества на 1 больше размерности разреза, делящего его на две несвязнае части (тополог.размерность отрезка-1, топол.разм. квадрата-2, плоскости-2);

3) Размерность самоподобия 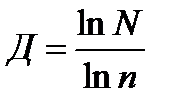. Размерность самоподобия – один из частных случаев фрактальной размерности.

Размерность Хаусдорфа — естественный способ определить размерность подмножества в метрическом пространстве.

Размерность Хаусдорфа согласуется с нашими обычными представлениями о размерности в тех случаях, когда эти обычные представления есть. Например, в трёхмерном евклидовом пространстве хаусдорфова размерность конечного множества равна нулю, размерность гладкой кривой — единице, размерность гладкой поверхности — двум и размерность множества ненулевого объёма — трём. Для более сложных (фрактальных) множеств размерность Хаусдорфа может не быть целым числом.

Основные понятия теории узлов

Модель узла - замкнутая, несамопересекающаяся кривая в пространстве.

Узел – это замкнутая линия в пространстве, гладкая или ломаная, которая может быть как угодно закручена и переплетена.

Под развязыванием узла будем понимать выпрямление этого отрезка путем деформации его в трехмерном пространстве.

тривиальный узел (окружность)

Изображение узла называется диаграммой узла.

Зацеплением называется конечный набор замкнутых непересекающихся ориентированных ломаных в пространстве.

Два узла называются изотопными (эквивалентными), если от одного к другому можно перейти последовательно выполняя преобразования, которые называются элементарными изотопиями.

Два узла изотопны, если один узел можно перевязать в другой, не разрезая его и не допуская самопересечений.

Вопрос. Полином Конвея

Наряду с обычными зацеплениями можно рассматривать ориентированные зацепления, то есть зацепления, на каждой компоненте которых задана ориентация – направление обхода. Для них точно так же определяются плоские диаграммы (с добавлением стрелочек, указывающих ориентацию компонент), а также движения Рейдемейстера (с согласованными ориентациями до и после движения).

Перейдем теперь к построению инвариантов ориентированных зацеплений. Рассмотрим три диаграммы ориентированных зацеплений, которые совпадают в некоторой малой окружности, а внутри нее отличаются так, как показано на рис. 4 сверху. Обозначим такие тройки диаграмм через L, L, L0 .

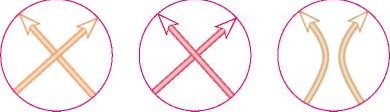
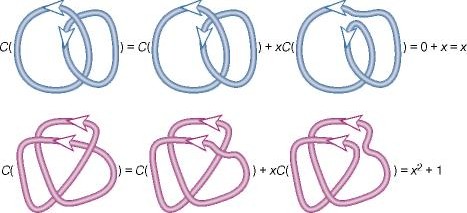
Рис. 4 Вычисление полинома Конвея

Можно показать, что существует единственный инвариант узла Cсо значениями в полиномах от одной переменной x, равный единице на тривиальном узле, нулю на тривиальном зацеплении из двух или более компоненты для каждой тройки диаграмм соотношению L, L, L0удовлетворяющийC( L)−C( L) =C( L0 ), называемому соотношением типа Конвея. Такой инвариант называется полиномом Конвея.

Полином Конвея удобен для вычисления. Пусть дана диаграмма Lзацепления с nперекрестками. Тогда, изменяя типы некоторых перекрестков (с прохода на переход и наоборот), можно превратить эту диаграмму в тривиальную. Это делается так. Рассмотрим проекцию одной из компонент зацепления и будем прокладывать веревку вдоль нее начиная с некоторой точки. В каждой вершине будем располагать второй виток веревки выше первого (то есть будем класть веревку каждый раз поверх себя). В итоге получим узел, который, очевидно, будет тривиальным. Далее расположим различные компоненты зацепления одна под другой. Получим диаграмму тривиального зацепления. Теперь у нас есть точный алгоритм вычисления полинома Конвея: мы выбираем диаграмму L' тривиального зацепления, получаемую из диаграммы Lзаменой некоторых типов перекрестков. Далее мы поочередно изменяем тип перекрестка в каждом из них и записываем соответствующее соотношение типа Конвея (в котором начальная и измененная диаграммы играют роль L₊, L_-, а роль диаграммы L0играет диаграмма с n−1перекрестком). В итоге мы получаем, что значение полинома Конвея C(L) равно значению полинома C(L'), то есть нулю или единице в зависимости от числа компонент, плюс сумма значений (со знаками плюс или минус) полинома Конвея на диаграммах с n−1 перекрестком.Таким образом, мы свели вычисление значения полинома Конвея на диаграмме с nперекрестками к вычислению на диаграммах с n−1 перекрестком. Продолжая в этом направлении, мы сведем это вычисление к диаграммам с 0 перекрестков, которые являются тривиальными узлами или зацеплениями.

Проиллюстрируем приведенный алгоритм на зацеплении Хопфа, а затем на правом трилистнике (см.рис. 4 внизу).

К сожалению, на левом трилистнике значение полинома Конвея такжеравно 1õ2 , то трилистник. Между тем существует много других инвариантов I(гораздо более мощных, чем полином Конвея), равных единице на тривиальном узле и основанных на соотношениях (также называемых соотношениями типа Конвея) вида aI( L₊) +bI( L_-) =cI( L0 ), где a,b, c– некоторые функции от одной или двух переменных. В случае полинома Конвея a= 1, b= −1, c= x. В частности, такие инварианты позволяют отличить левый трилистник от правого. Приведем список наиболее известных из этих инвариантов:

полином Джонса от одной переменной

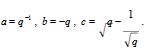
полином HOMFLY от двух переменных a= x, b= −t, c= 1. Наиболее сильный из этих инвариантов – полином Джонса от двух переменных λ, q, в котором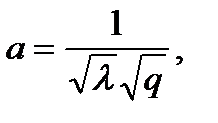

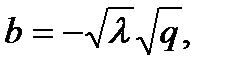
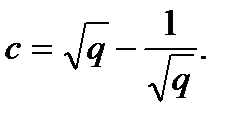
Примеры вычисления полинома Конвея.

ИЛИ:

Основные понятия и факты теории кос

Теория кос – это реальная и живая наука, возникшая в 20-ых годах прошлого века тогда еще молодым немецким алгебраистом Э. Артином по заказу ткацкой фабрики: он выполнял, как бы сказали сегодня, хоздоговорную работу для этого предприятия.

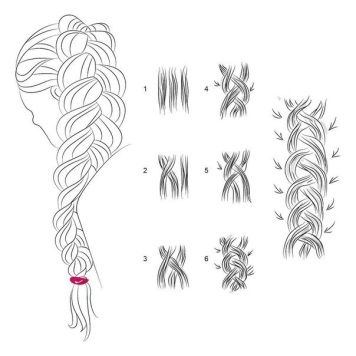
Приведем примеры кос (рис. 1).

К1	К2	К3	К4
«Девичья коса»	Тривиальная коса	Крашеная коса	Циклическая коса
Диаграммы – проекция косы на плоскость
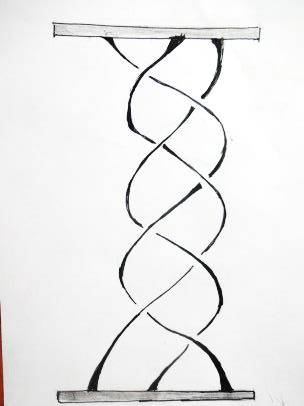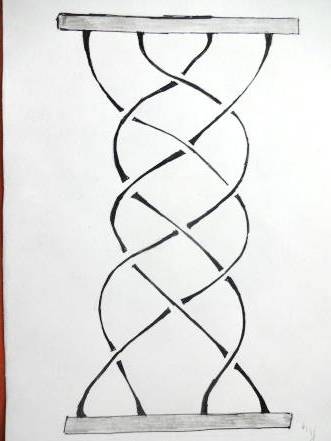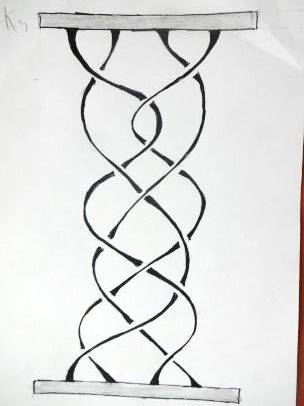Рис. 1. Примеры кос из трех и четырех нитей

Косу можно себе представлять так: в верхний и нижний край вертикальной доски вбито по n гвоздиков (n может равняться 1, 2, 3, …) – каждый из гвоздиков верхнего основания соединен нитью с одним из гвоздиков нижнего; нити попарно не пересекаются и все время должны опускаться вниз (нить не имеет права, повернувшись, начать подниматься вверх: фигуры на рисунке 2, например, косами не являются).

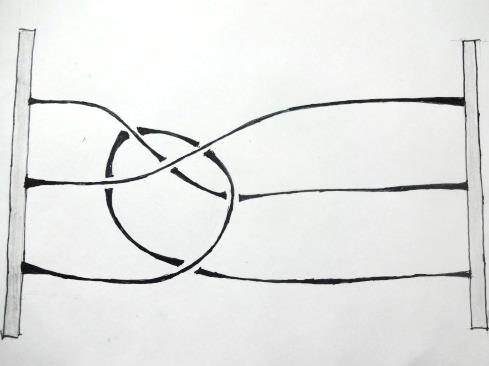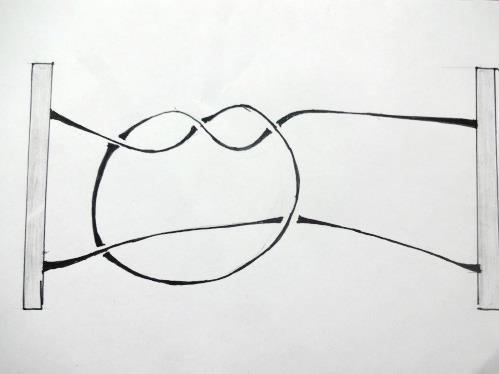Рис. 2. Эти фигуры не являются косами: их нити имеют восходящий характер

Две косы считаются эквивалентными (т. е. одинаковыми), если одну можно превратить в точную копию другой, двигая нити (без разрывов и склеиваний) так, чтобы каждая точка каждой нити перемещалась только в горизонтальной плоскости. Такое движение показано на рисунке 3.

Рис. 3. Геометрическое доказательство тривиальности косы

Коса К тривиальна, ибо она легко превращается (см. рис. 3) в косу из четырех вертикальных нитей).

На рисунке 1 вверху у начала каждой нити указан ее порядковый номер. Внизу снова указан номер каждой нити – но здесь номера не обязаны идти по порядку: каждой косе соответствует перестановка номеров ее нитей. Так, косами К₁, К₃, К₄ на рисунке 1 отвечают перестановки:

, , .
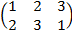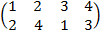Среди кос на рисунке 1 выделяется крашеная коса К₃: так она называется вовсе не потому, что нарисовали ее нити разными цветами: крашеной называется любая коса, которой отвечает тождественная перестановка , т. е. коса, сохраняющая порядок номеров нитей.

Тривиальная коса, все нити которой вертикальные прямые является частным случаем крашеной косы.

Среди кос следует выделить, кроме крашеных, в известном смысле противоположные им - циклические косы: это косы, переставляющие все номера нитей по единому циклу, как это делает коса К₄: 1®2® 4 ®3 ®1.

Тривиальные соотношения

SjSj- 1 = Sj-1S j = 1 , Sj.1=1 .Sj=S j(j=1, 2,…, n-1).

Доказательство.

Любая коса представляется в виде произведения элементарных кос S1,S2,…,Sn-1и обратных к ним,например,

K1=S1S2-1S1S2-1S1S2-1., K3=S2S1S3-1S1-1S3S2-1S1S3S1-1S3-1.

Узел - замкнутая кривая без самопересечения,узел можно описать двумерной диаграммой.

Конечный набор замкнутых непересекающихся ориентированных ломаных в прост­ранстве называетсязацеплением.

Два узла называются эквивалентными, если узел, сжимая, растягивая, двигая в пространстве (без разрывов и склеек), можно превратить в другой.

Главной проблемой теории узлов является поиск инварианта, препятствующего распутыванию.

Теорема.

Теорема Рейдемейстера

Два узла эквивалентны тогда и только тогда, когда от диаграммы одного узла к диаграмме другого можно перейти с помощью конечного числа двумерных элементарных операций 1, 2, 3 (рис.4).

Можно ли по любой паре диаграмм узнать, эквивалентны узлы или нет, можно ли их распутать?

Оказывается можно, для каждого узла и зацепления можно построить соответствующий ему инвариант. Инварианты позволяют не только различать неодинаковые узлы и отличать узлы от незаузленных петель, но и классифицировать косы. По-разному деформированным вариантам одного и того же узла отвечает один и тот же инвариант; узлы, соответствующие разным инвариантам различны. Но два узла с одним и тем же инвариантом необязательно эквивалентны. Если инвариант узла не равен инварианту тривиального узла, то данный узел не может быть тривиальным и его нельзя распутать. Рассмотрим самые известные инварианты и вычислим их для некоторых зацеплений.

Многочлен Александера.

Этот многочлен был открыт американским математиком Александером в 1928 году. Он строится в соответствии с числом пересечений каждого вида, имеющихся на диаграмме узла. Например, узлу «трилистник» соответствует многочлен Δ_K(t)=t–1–1/t.

Многочлен Конвея

Р_L (х) - это многочлен от переменной х с целыми коэффициентами.

Теорема.

Для каждого узла или зацепления Lполином РL(х) существует и однозначно определяет­ся следующими тремя аксиомами.

Аксиома 1.

Эквивалентным диаграммам L и L’ отвечает один и тот же полином: РL(х)=РL’(х).

Аксиома 2.

Тривиальному узлу отвечает по­лином, равный 1:Ро(х)==1.

Аксиома 3.

Трем зацеплениям L⁺, L-, L°, которые всюду одинаковы, кроме кружочка, где они выгля­дят так, как показано на рисунке 5, отвечают полиномы, связанные соот­ношением

РL+(х)-РL-(х)=х.РL0(х).

рис.5

Теорема.

Для распавшегося зацепления Р_L (х) =О.

Вычислим полиномы Конвея для некоторых узлов и зацеплений.

а) Для двух незацепленных окружностей.

L+- диаграмма тривиального узла с одной двой­ной точкой, L°- диаграмма двух незацепленных окруж­ностей. Из аксиом I и II следует, что РL+(х) = 1.

Если заменить двойную точку диаграммы L+на противоположную, а затем двойную точку уничтожить (аксиома III), то мы полу­чим диаграмму тривиального узла L-и пару незацепленных окруж­ностей L°.

По аксиоме III, получим РL+(х)-РL-(х)=х.РL0(х),1—1=х.РL0(х),РL0(х)=0.

б) Для двух зацепленных окружностей (правое зацепление):

Применяя аксиому III к правой двойной точке, получаем диаграмму L-, эквивалентную паре незацепленных окружностей, и тривиальный узел (с одной двойной точкой) L°.

Используя аксиому I и предыдущий подсчет, получаем РL-(х)=0.

Затем по аксиомам I и II получаем РL0(х)=1.

Подставляя эти значения в соотноше­ние аксиомы III, получим РL+(х)=х.Для левого зацепления полином равен –х

в) Для узла «трилистник»

Р_L(х)=1,т.к. распутывается в тривиальный узел.
Р_L⁰(х) =- х, т.к. распутывается в левое зацепление двух окружностей, значит, Р_L (х) = 1 - х² по аксиоме 3.

г) Для восьмерки.

Р_L (х) = х, так как распутывается в правое зацепление двух окружностей.
Р_L (х) = 1, так как распутывается в тривиальный узел.

Поэтому P_L’ (x) = 2х по аксиоме 3.

д) Для проколотой восьмеркиР_L (х) = х, так как распутывается в правое зацепление двух окружностей.

Пусть зацепление L1 = L⁰.Тогда Р_L1(х)= 1. Р_L1⁰(х) = х, так как распутывается в правостороннее зацепление двух окружностей.

Значит, Р_L1 (х) = х² + 1. В итоге Р_L (х) = х³+ 2х .

Даже небольшое число проведенных вычислений показывает, что полином Конвея — достаточно тонкий инстру­мент, позволяющий различать узлы и зацепления и устанавливать их нетри­виальность. Посчитав, например, по­линомы трилистника, восьмерки, и убедившись, что эти полиномы не равны 0 или 1, мы доказали, что их нельзя распу­тать. Разумеется, эти доказательства верны только в том случае, если уже установлен факт существования и единственности полинома Конвея для каждого узла и зацепления.

Алгебра кос

Узлы и косы можно рассматривать как алгебраические объекты: их можно умножать. Возьмем две косы a и bc одинаковым числом нитей и соединим нижние концы нитей первой косы с верхними концами второй косы; полученную косу, сжатую в два раза в вертикальном направлении, называют произведением этих двух кос и обозначают ab.

Умножение ассоциативно, т.е. для любых трех кос a, b, c косы (a∙b) ∙c и a∙ (b∙c) эквивалентны. Тривиальная коса играет роль единицы. Чтобы получить обратную косу (т.е. a^-1), нужно зеркально отразить косу a относительно горизонтальной плоскости. Умножение кос некоммутативно.

Иными словами, косы образуют группу. Эта группа некоммутативна.

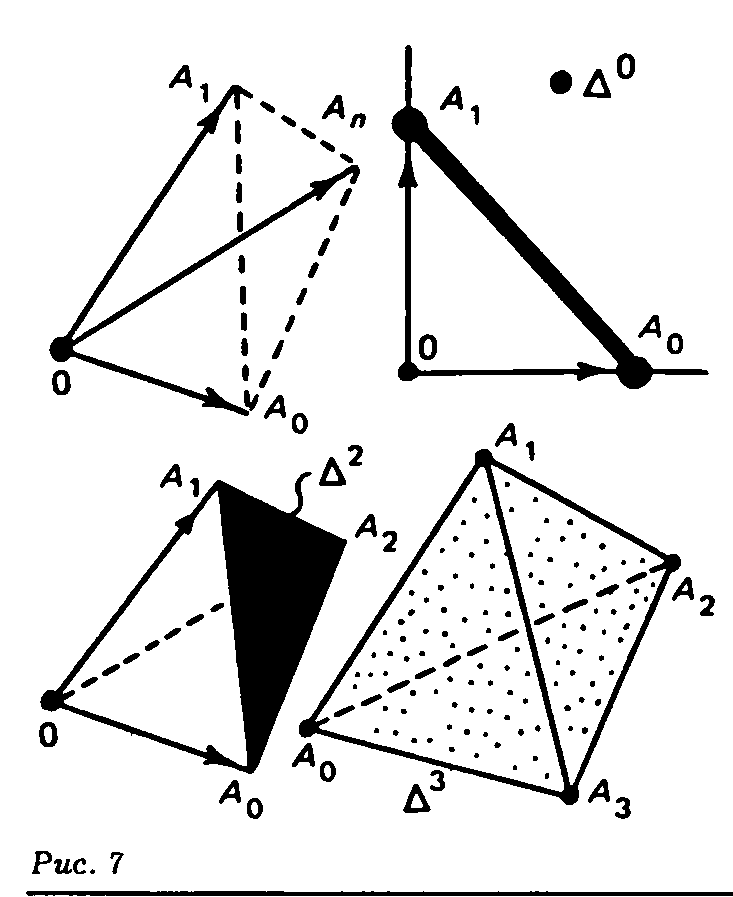
Прямолинейные и топологические симплексы. Примеры.

Симплекс 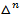является выпуклой линейной оболочкой точек . Поэтому он иногда называется прямолинейным( или евклидовым) симплексом.

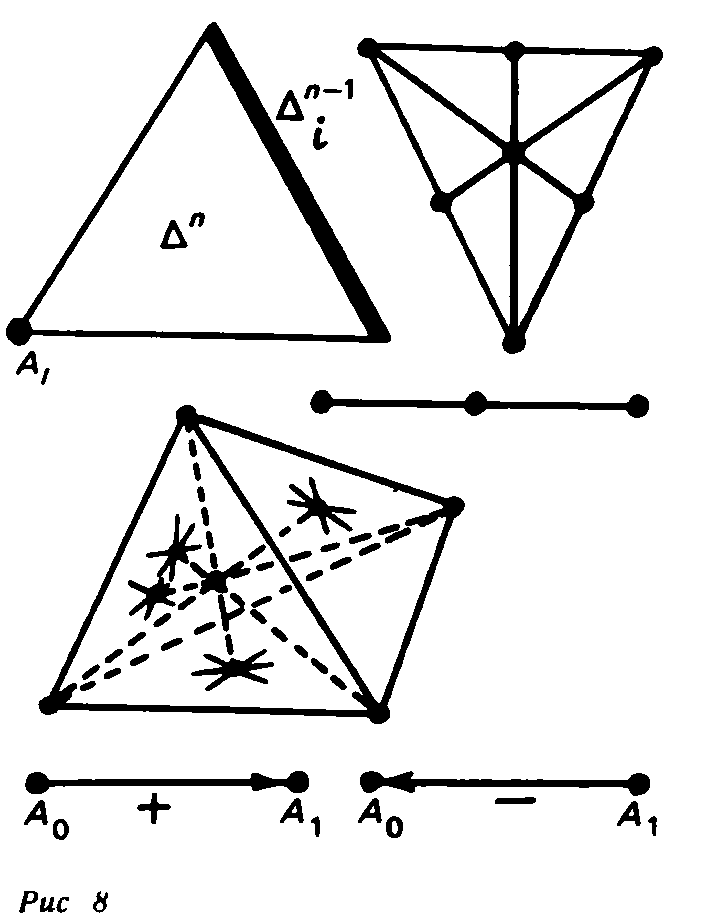
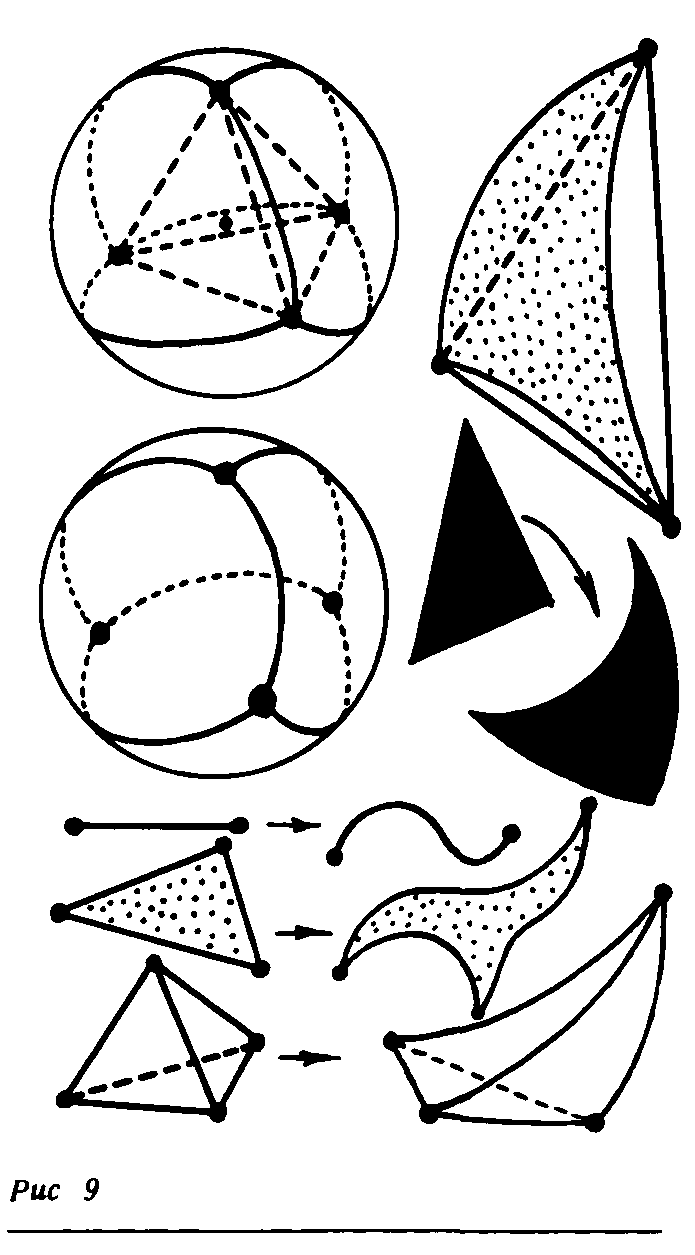
Вопрос 38. Международное сравнительное мониторинговое исследование качества математического и естественнонаучного образования TIMSS.

Международное мониторинговое исследование качества школьного математического и естественнонаучного образования TIMSS(англ. TIMSS — Trends in Mathematics and Science Study) — это программа, организованная Международной ассоциацией по оценке учебных достижений IEA. Данное исследование позволяет сравнить уровень и качество математического и естественнонаучного образования учащихся 4-х классов начальной школы и учащихся 8-х классов в различных странах мира, а также выявить различия в национальных системах образования.

Исследование проводится циклично — один раз в четыре года, и к настоящему времени было проведено шесть раз: в 1995, 1999, 2003, 2007, 2011 и 2015 годах.

При этом трижды с 1995 года (последний раз в 2015 году) проводилось «расширенное» исследование (Advanced TIMSS), включающее в себя изучение достижений обучающихся последнего класса школы (в России это 11-й, в США — 12-й и т. д.)

Краткая информация об исследовании TIMSS

Основной целью международного исследования TIMSS является сравнительная оценка качества математического и естественнонаучного образования в начальной и основной школе. Каждые четыре года оцениваются образовательные достижения учащихся 4 и 8 классов, включающие не только их знания и умения, но и отношения к предметам, интересы и мотивации к обучению. Исследование спланировано таким образом, что его результаты позволяют отслеживать тенденции в математическом и естественнонаучном образовании участвующих стран каждые 4 года, когда учащиеся 4 классов становятся учащимися 8 класса. Таким образом, осуществляется мониторинг учебных достижений учащихся начальной и основной школы, а также изменений, происходящих в математическом и естественнонаучном образовании при переходе из начальной в основную школу.

Дополнительно изучаются особенности содержания школьного математического и естественнонаучного образования в странах-участницах исследования, особенности учебного процесса, а также факторы, связанные с характеристиками образовательных учреждений, учителей, учащихся и их семей. Для этого дополнительно к международному тестированию проводится анкетирование учащихся, учителей и администрации школ, участвовавших в исследовании. Полученные данные позволяют выявить факторы, влияющие на результаты тестирования, и объяснить состояние математического и естественнонаучного образования в странах-участницах исследования.

В проведении исследования и разработке его инструментария принимают участие многие научно-исследовательские центры и профессиональные организации мира.

В России данное исследование осуществляется Центром оценки качества образования Института содержания и методов обучения Российской академии образования(ИСМО РАО) при активном участии Министерства образования и науки РФ и органов управления образованием регионов.

Характеристика инструментария исследования

В качестве основы для разработки инструментария исследования TIMSS используется специальный рамочный документ «TIMSS Assessment Frameworks and Specifications», в котором определены общие подходы к оценке образовательных достижений по математике и естествознанию, разработке тестов и тестовых заданий, описано проверяемое содержание по математике и естествознанию, а также виды познавательной деятельности, которые должны продемонстрировать учащиеся при выполнении заданий, перечислены основные факторы, характеризующие учащихся, учителей и образовательные учреждения, для анализа которых собирается информация в процессе анкетирования, приведены примеры заданий.

Инструментарий международного исследования TIMSS включает:

тесты достижений;

анкеты (для учащихся, учителей, администрации образовательного учреждения, экспертов в области образования, наблюдателей за качеством исследования);

методическое обеспечение (руководство для национальных координаторов по организации и проведению исследования, руководство по формированию выборки, руководство для школьных координаторов, руководство по проведению тестирования, руководства по проверке заданий со свободными ответами, руководство по вводу данных и др.);

программное обеспечение (по отбору классов и учащихся, по вводу данных).

Международные тесты разрабатываются на основе следующих принципов:

адекватный охват проверяемого содержания и видов учебно-познавательной деятельности;

максимальное соответствие содержания международных тестов изучаемому материалу в большинстве стран-участниц;

обеспечение связи тестов;

значимость проверяемого содержания с точки зрения развития математического и естественнонаучного образования;

соответствие возрастным особенностям учащихся, для оценки достижений которых разрабатывался тест;

соответствие требованиям, предъявляемым к массовым исследованиям.

Для оценки математической и естественнонаучной подготовки учащихся в тесты (в каждый вариант) включаются задания и по математике, и по естествознанию. Используются задания разного типа (с выбором ответа, с кратким и полным развернутым ответом, практические задания).

Вопрос 39. Международное исследование образовательных достижений PISA

Международная программа по оценке образовательных достижений учащихся PISA (Programme for International Student Assessment) является мониторинговым исследованием качест