Главный момент относительно центра
– векторная сумма моментов всех сил, приложенных к телу относительно того же центра.
14) Теорема Шаля:
Плоскую фигуру можно переместить из одного положения в любое другое положение на плоскости одним поворотом этой фигуры вокруг некоторого неподвижного центра. Этот центр на неподвижной плоскости, совпадает см.ц.с. и называется мгновенным центром вращений (ось вращений). При движении плоской фигуры м.ц.с. непрерывно изменяет свое положение. Геометрическое место м.ц.с., отмеченных на неподвижной плоскости, называется неподвижной центроидой. Геометрическое место м.ц.с., отмеченных на плоскости фигуры, называется подвижной центроидой (колесо катится по прямой: неподвижная центроида – прямая, подвижная – окружность). При движении плоской фигуры подвижная центроида катится без скольжения по неподвижной центроиде (теорема Пуансо).
Теорема Вариньона
– если плоская система сил приводится к равнодействующей, то ее момент относительно какой-либо точки равен алгебраической (т.е. с учетом знака) сумме моментов всех сил относительно той же точки.
16-17) Условия равновесия пространственной системы сил:
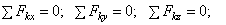 или
или 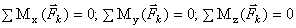 .
.
18)Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю.
19) 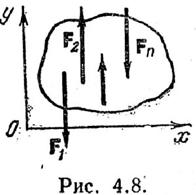
Необходимым и достаточным условием равновесия системы сил является равенство нулю главного вектора и главного момента. Для плоской системы сил эти условия получают вид Fo=åFk=0, МОz=åМoz(Fk)=0, (5.15), где О– произвольная точка в плоскости действия сил. Получим: Fox=åFkx=F1x+F2x+…+Fnx=0, Pox=åFky=F1y+F2y+…+Fny=0, МОz=åMOz(Fk)=Moz(F1)+Moz(F2)+…+Moz(Fn)=0, т. е. для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на две координатные оси и алгебраическая сумма моментов всех сил относительно произвольной точки равнялись нулю. Второй формой уравнения равновесия является равенство нулю алгебраических сумм моментов всех сил относительно любых трех точек, не лежащих на одной прямой;
20)Системы, внутренние силы в которых от заданной нагрузки можно определить из уравнений их равновесия (уравнений статики), называются статически определимыми системами.
Система статически н е о п р е д е л и м а, если число реакций ее связей и внутренних сил превышает число независимых уравнений равновесия, которые могут быть составлены для этой системы.
Разность числа неизвестных сил и числа независимых уравнений равновесия называют с т е п е н ь ю с т а т и ч е с к о й н е о п р е д е л и м о с т и системы.
Уравнения равновесия дополняют уравнениями перемещений. Их составляют, рассматривая систему в деформированном состоянии и устанавливая соотношения между перемещениями ее сечений или узлов.
| 21) |
Для записи условия равновесия системы, состоящей из твёрдых тел, систему разделяют на отдельные части, и записывают уравнения равновесия как для всей системы, так и для её частей[1]. При этом возможны несколько эквивалентных вариантов записи условий равновесия в зависимости от выбора частей системы, для которых записываются уравнения.
22) Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
xc = (∑ Gixi) / ∑ Gi;
(1) yc = (∑ Giyi) / ∑ Gi;
zc = (∑ Gizi) / ∑ Gi.
23)Кинематика изучает движение тел, без учета причин, которыми обусловлено это движение.
Основными задачами кинематики являются:
1. Описание с помощью формул, таблиц и графиков совершаемых телом движений.
2. Определение кинематических величин, характеризующих это движение.
Для описания движений в кинематике вводится ряд специальных понятий (материальная точка, абсолютно твердое тело, система отсчета, траектория и т.д.) и величин (путь, перемещение, скорость, ускорение и т.д.)
Механическим движением называют изменение положения тела относительно других тел в пространстве с течением времени.
Тело, относительно которого рассматривается движение других тел, называется телом отсчета.
Систему координат и прибор для отсчета времени, связанные с телом отсчета, называют системой отсчета.
Тело, деформациями которого в данных условиях движения можно пренебречь, называют абсолютно твердым телом.
Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой.
Линию, описываемую материальной точкой при своем движении, называют траекторией.
Любое движение твердого тела можно разделить на два вида движения: поступательное и вращательное.
Поступательным называют такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе.
Вращательным называют такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. (Ось вращения может находиться и вне тела).
24) 3. Векторный способ.
Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторого начала в данную точку (рис. 2). В этом случае для описания движения необходимо задать:
а) начало отсчета радиус-вектора r;
б) начало отсчета времени t;
в) закон движения точки r(t).
Поскольку задание одной векторной величины r эквивалентно заданию трех ее проекций x, y, z на оси координат, от векторного способа легко перейти к координатному. Если ввести единичные векторы i, j, k( i= j = k= 1), направленные соответственно вдоль осей x, y и z (рис. 2), то, очевидно, закон движения может быть представлен в виде*)
r(t) = x(t)i+y(t)j+z(t)k. (1)
Преимущество векторной формы записи перед координатной в компактности (вместо трех величин оперируют с одной) и часто в большей наглядности.
Координатный способ.
Это наиболее универсальный и исчерпывающий способ описания движения. Он предполагает задание:
а) системы координат (не обязательно декартовой) q1, q2, q3;
б) начало отсчета времени t;
в) закона движения точки, т.е. функций q1(t), q2(t), q3(t).
Говоря о координатах точки, мы всегда будем иметь в виду (если не оговорено противное) ее декартовы координаты.
26)Естественный способ.
Этим способом пользуются, если известна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве. При естественном способе необходимо задать (рис. 1):
а) траекторию движения (относительно какой-либо системы координат);
б) произвольную точку на ней нуль, от которого отсчитывают расстояние S до движущейся частицы вдоль траектории;
в) положительное направление отсчета S (при смещении точки М в противоположном направлении S отрицательно);
г) начало отсчета времени t;
д) функцию S(t), которая называется законом движения**) точки.
27)Скоростью точки в данный момент времени называется вектор v, равный первой производной от ее радиуса-вектораr по времени:
v = dr/dt = 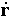 ;
;
(Производную по времени принято в механике обозначать точкой над дифференцируемой величиной).
Вектор скорости, характеризующий изменение с течением времени модуля и направления радиуса-вектора точки, направлен по касательной к траектории точки в сторону ее движения.
При прямолинейном движении вектор скорости v все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь по величине; при криволинейном движении кроме модуля все время изменяется и направление вектора скорости точки.
В качестве единиц измерения скорости применяют обычно м/с или км/ч.
Ускорением точки в данный момент времени называется вектор a, равный первой производной от вектора скорости v или второй производной от ее радиуса-вектораr по времени:
a = dv/dt = dr2/dt2 ;илиa = 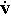 =
= 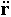 .
.
Ускорение точки, как векторная величина, характеризует изменение с течением времени модуля и направления вектора скорости точки.
Рассмотрим, как располагается вектор a по отношению к траектории точки.
При прямолинейном движении вектор a направлен вдоль прямой, по которой движется точка. Если траекторией является пространственная кривая, то вектор a направлен в сторону вогнутости траектории и лежит в соприкасающейся плоскости. Так называют плоскость, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении dr = vdt движущейся точки (подробнее это понятие изложено при задании движения точки естественным способом). Для пространственной кривой в каждой ее точке будет, вообще говоря, своя соприкасающаяся плоскость. Для плоской кривой соприкасающаяся плоскость совпадает с плоскостью этой кривой и является общей для всех ее точек.
В качестве единицы измерения ускорения применяется обычно м/с2.
28)Определение скорости точки
Проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени:
vx = dx / dt; vy = dy / dt; vz = dz / dt;
или
vx = 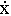 ; vy =
; vy = 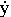 ; vz =
; vz = 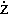 ,
,
где точка над координатой означает символ дифференцирования по времени.
Модуль и направляющие косинусы (косинусы углов, которые образует вектор v с координатными осями Ox, Oy, Oz) вектора v выражаются через его проекции по следующим формулам:
v =( vx2 + vy2 + vz2) 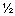 ; cos(v,Ox) = vx / v; cos(v,Oy) = vy / v; cos(v,Oz) = vz / v.
; cos(v,Ox) = vx / v; cos(v,Oy) = vy / v; cos(v,Oz) = vz / v.
Определение ускорения точки
Проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени:
ax = dvx / dt = d2x / dt2; ay = dvy / dt = d2y / dt2; az = dvz / dt = d2z / dt2;
или
ax = 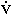 x=
x= 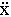 ; ay =
; ay = 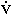 y=
y= 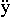 ; az =
; az = 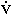 z=
z= 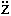 ;
;
Модуль и направляющие косинусы вектора ускорения a выражаются через его проекции по следующим формулам:
a =( va2 + ay2 + az2) 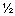 ; cos(a,Ox) = ax / a; cos(a,Oy) = ay / a; cos(a,Oz) = az / a.
; cos(a,Ox) = ax / a; cos(a,Oy) = ay / a; cos(a,Oz) = az / a.
29) Вектор ускорения a точки лежит в соприкасающейся плоскости P 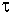 n и определяется двумя проекциями
n и определяется двумя проекциями 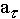 и an (ab = 0):
и an (ab = 0):
проекция ускорения точки на касательную равна первой производной от алгебраической скорости или второй производной от криволинейной координаты точки по времени:
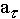 = d
= d 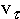 / dt = d2s /dt2или
/ dt = d2s /dt2или 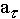 =
= 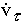 =
= 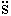 .
.
проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой:
an = v2 / 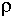 .
.
Величины 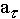 и an соответственно называют касательным и нормальным ускорениями точки.
и an соответственно называют касательным и нормальным ускорениями точки.
30. определение скорости и ускорения точки при координатном задания её движения.
Определение ускорения при координатном способе задания движения
Вектор ускорения точки 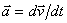 в проекции на оси получаем:
в проекции на оси получаем:
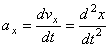 ,
, 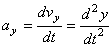 ,
, 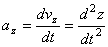
или
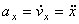 ,
, 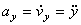 ,
, 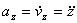 ,
,
т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул
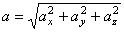 ;
;
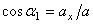 ,
, 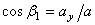 ,
, 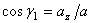 ,
,
где 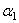 ,
, 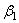 ,
, 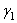 - углы, образуемые вектором ускорения с координатными осями.
- углы, образуемые вектором ускорения с координатными осями.
Определение скорости точки при координатном способе задания движения
Вектор скорости точки 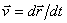 , учитывая, что
, учитывая, что 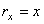 ,
, 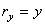 ,
, 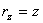 , найдем:
, найдем:
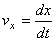 ,
, 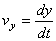 ,
, 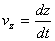 .
.
Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
Зная проекции скорости, найдем ее модуль и направление (т.е. углы 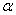 ,
, 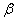 ,
, 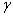 , которые вектор
, которые вектор 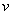 образует с координатными осями) по формулам
образует с координатными осями) по формулам
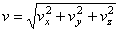 ;
;
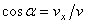 ,
, 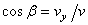 ,
, 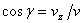 .
.
Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени.
Направлен вектор скорости по касательной к траектории, которая нам наперед известна.
31.Равномерное и равнопеременное движения точки.
Равноме́рное движе́ние — механическое движение, при котором тело за любые равные отрезки времени проходит равные перемещения. Равномерное движение материальной точки — это движение, при котором скорость точки остаётся неизменной. Перемещение, пройденное точкой за время 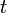 , задаётся в этом случае формулой
, задаётся в этом случае формулой 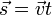 .
.
Прямолинейное равномерное движение — это движение, при котором тело (точка) за любые равные и бесконечно малые промежутки времени проходит одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости на время:
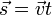 .
.
Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты 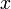 точки от времени является линейной:
точки от времени является линейной:
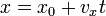 ,
,
где 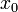 — начальная координата точки,
— начальная координата точки, 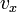 — проекция вектора скорости на координатную ось.
— проекция вектора скорости на координатную ось.
Точка, рассматриваемая в инерциальной системе отсчёта, находится в состоянии равномерного прямолинейного движения, если векторная сумма всех сил, приложенных к точке, равна нулю.
Если вектор at=const (касательное ускорение постоянно как по модулю, так и по направлению), то an=0. Такое движение называется равнопеременным и прямолинейным.
Если же постоянным остается только числовое значение касательного уравнения
at = dv/dt = f'(t) = const,
то an≠0 и такое движение точки называется равнопеременным криволинейным.
При |at|>0 движение точки называется равноускоренным, а при |at|<0 –равнозамедленным.
Уравнение равнопеременного движения независимо от его траектории имеет вид
(1)s = s0 + v0t + att2 / 2.
Здесь s0 – расстояние точки от исходного положения в момент начала отсчета; v0 – начальная скорость и at – касательное ускорение – величины численно постоянные, a s и t – переменные.
Числовое значение скорости точки в любой момент времени определяется из уравнения
(2)v = v0 + att.
Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s0, v0, at и три переменные: s, v, t.
Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).
Если неизвестные входят в оба основных уравнения, например, неизвестны at и t, то для удобства решения таких задач выведены вспомогательные формулы:
после исключения at из (1) и (2)
(3)s = s0 + (v + v0)t / 2;
после исключения t из (1) и (2)
(4)s = s0 + (v2 - v02) / (2at).
В частном случае, когда начальные величины s0=0 и v0=0 (равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:
(5)s = att2 / 2;
(6)v = att;
(7)s = vt / 2;
(8)s = v2 / (2at).
Уравнения (5) и (6) являются основными, а уравнения (7) и (8) – вспомогательными.
Равноускоренное движение из состояния покоя, происходящее под действием только силы тяжести, называется свободным падением. К этому движению применимы формулы (5)–(8), причем
at = g = 9,81 м/сек2 ≈ 9,8 м/сек2.
32. Поступательное движение твердого тела.
Поступательное движение — РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ точки - движение, при к-ром касат. ускорение wтточки (в случае прямолинейного движения полное ускорение w)постоянно. Закон Р. д. точки и закон изменения её скорости u при этом движении даются равенствами:
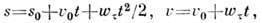
где s - измеренное вдоль дуги траектории расстояние точки от выбранного на траектории начала отсчёта, t - время, s0 - значение s в нач. момент времени t = = 0. 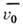 - нач. скорость точки. Когда знаки u и w одинаковы, Р. д. является ускоренным, а когда разные - замедленным.
- нач. скорость точки. Когда знаки u и w одинаковы, Р. д. является ускоренным, а когда разные - замедленным.
При поступат. Р. д. твёрдого тела всё сказанное относится к каждой точке тела; при равномерном вращении вокруг неподвижной оси угл. ускорение e тела постоянно, а закон вращения и закон изменения угл. скорости w тела даются равенствами
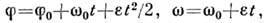
где f - угол поворота тела, f0 - значение f в нач. момент времени t = 0, w0 - нач. угл. скорость тела. Когда знаки w и e совпадают, вращение является ускоренным, а когда не совпадают - замедленным.
33.Вращательное движение твердого тела. Угловая скорость и угловое ускорение тела.
