Классификация задач нелинейнойоптимизации и методовихрешения.

С точки зрения наличия или отсутствия ограничений ЗНО подразделяются на задачи условной и безусловной оптимизации.

Классическая задача условной нелинейной оптимизации формулируется следующим образом.

Найти такие значения переменных 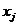, , 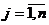которые удовлетворяли бы ограничениям

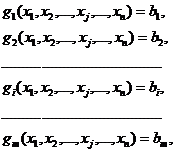(1)

и обращали бы в минимум или максимум целевую функцию

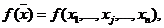(2)

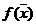где и 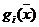, 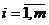– непрерывные, дважды дифференцируемые функции,

b_i– некоторые константы.

В общем случае для задачи нелинейной оптимизации характерно то, что в ограничениях вида (1) присутствует условие ³ либо £ вместо требования строгого равенства.

Cточки зрениячисла переменных (аргументов целевой функции) ЗНО подразделяются на задачи одномерной и многомерной оптимизации.

С точки зрения числа экстремумов целевой функции ЗНО подразделяются на одноэкстремальные и многоэкстремальные. В первом случае ЗНО относятся к так называемым задачам выпуклой оптимизации, поскольку целевая функция

f(x) удовлетворяет условию выпуклости

"x_i, x_j: f(ax_i + (1–a)x_j) £af(x_i) + (1–a)f(x_j), 0 £a< 1,

где x_i, x_j– произвольные значения аргумента из области определения функции f(x).

Для того чтобы установить, является ли целевая функция выпуклой в окрестности данной точки, пользуются критерием Сильвестра, согласно которому, если все главные миноры матрицы вторых частных производных целевой функции в данной точке больше нуля, то данная целевая функция – выпукла.^* Примером задачи выпуклой оптимизации является задача квадратичной оптимизации, целевая функция которой представляет собой квадратичную функцию, а ограничения заданы в виде линейных неравенств.

Для одноэкстремальных задач, в противоположность многоэкстремальным, локальный минимум совпадает с глобальным. При этом для задач выпуклой

оптимизации характерным является наличие правила, следуя которому, за опре-

делённое число шагов можно достичь оптимального решения путём

__________________________________________________________________________

* – Напомним, что минором r-го порядка квадратной матрицы порядка n (r £ n) называется определитель, составленный из элементов, находящихся на пересечении каких-либо r строк и r столбцов матрицы, а главными минорами матрицы называются миноры, образованные первыми её r строками r столбцами.

упорядочения перебора вариантов решений.

В то же время, для задач невыпуклой оптимизации такого правила нет, поэтому в этом случае имеет место неупорядоченный перебор подозреваемых на экстремум вариантов решений. При этом каждый из вариантов, подозреваемый на локальный экстремум, должен рассматриваться как вариант, подозреваемый на глобальный экстремум.

Что касается методов решения ЗНО, то с точки зренияхарактера получения решения они подразделяются на прямые (аналитические) методы и приближённые (численные), основанные на итерационных поисковых алгоритмах (или просто поисковые).

Примером прямого метода является метод неопределённых множителей Лагранжа, который предполагает сведение задачи условной оптимизации с ограничениями равенствами к задаче безусловной оптимизации, а также классический метод поиска экстремума функции (еслиречьидёт о задаче безусловной оптимизации), который предполагает вычисление производной целевой функции и решение уравнения f‘(x) = 0 (в случае одномерной оптимизации) или вычисление частных производных целевойфункции по каждой переменной и решение системы уравнений 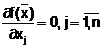(в случае многомерной оптимизации)^*.

Однако этот классический подход не всегда оказывается приемлемым, поскольку найти корни уравнения, получившегося в результате вычисления производной целевой функции, часто не представляется возможным из-за вида самой этой функции. Поэтому подавляющее большинство методов решения ЗНО относятся к категории поисковых, идея которых состоит в том, что произвольно выбирается начальная точка (вектор начальных значений искомых переменных), а затем в соответствии с некоторым правилом определяется направление и величина шага движения к следующей точке и т.д. до тех пор, пока не будет найдено оптимальное решение с заданной точностью приближения. Примером поисковых методов являются градиентные методы, наиболее распространённым из которых является метод наискорейшего спуска, часто применяемый для минимизации выпуклых функций многих переменных.

С точки зрениявычисленияпроизводныхфункцииметоды решения ЗНО подразделяются методы, которые предполагают вычисление производных, и методы, не предусматривающие вычисление производных. Прямые методы всегда предполагают вычисление производных, в то время как поисковые методы могут основываться на их вычислении, а могут и не основываться. Для последнего случая представителями этих методов являются градиентные и так называемые релаксационные методы соответственно.

______________________________________________________________________________________________

* –Следует заметить, чторавенство нулю частныхпроизводныхцелевойфункции в даннойточке (называемойстационарнойточкой) являетсятольконеобходимым, но не достаточнымусловиемсуществованияэкстремума в этойточке, или, иначе, не всякаястационарная точка являетсяточкойэкстремума. Для выяснения характера стационарной точки определяется матрица вторых частных производных целевой функции в данной точке (матрица Гессе) и рассчитываются её главные миноры от первого до n-го порядка. Если матрица Гессе положительно определённая (все её главные миноры положительны), то в данной точке находится минимум функции, а если матрица Гессе отрицательно определённая (когда знаки главных миноров чередуются при том, что главный минор первого порядка отрицательный), то в данной точке находится максимум функции. В противном случае полученная стационарная точка является седловойточкой. Важно также отметить, что сказанное касается только непрерывных гладких функций, т.е. таких, у которых нет точек перегиба (в случае функции одной переменной), в которых производная равна нулю. В тоже время, и такие точки могут быть точками экстремума функции.

При этом среди методов, которые предполагают вычисление производных, есть такие, которые используют только первые производные, а также те, которые используют вторые производные. К числу первых относятся градиентные методы, а представителем вторых является метод Ньютона.

Что касается релаксационных методов, не использующих вычисление производных, то их общая идея состоит в том, что в процессе поиска оптимального решения ищется минимум целевой функции по одной переменной, в то время как другие переменные фиксируются (остаются постоянными); затем отыскивается минимум функции по другой переменной при фиксировании остальных, в том числе и нового значения той переменной, по которой на предыдущем шаге искался минимум, и т.д.

В свою очередь поисковые методы с точки зрения присутствия элемента случайности в алгоритме поиска разделяются на детерминированные методы и методы случайного поиска.