Векторное представление синусоидальных токов и напряжений.

Формулировка закона Ома

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого проводника и обратно пропорциональна его сопротивлению:

I = U / R; [A = В / Ом]

Ом установил, что сопротивление прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.

R = ρl / S,
где ρ - удельное сопротивление, l - длина проводника, S - площадь поперечного сечения проводника.

1. Законы Кирхгофа

1-й закон для узла: Алгебраическая сумма токов в узле равна нулю

2-й закон для контуров:Алгебраическая сумма ЭДС в замкнутом контуре равняется алгебраической сумме падений напряжений на всех участках контура.

8. Энергетический баланс в электрической цепи постоянного тока.

В любой электрической цепи должен соблюдаться энергетический баланс - баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

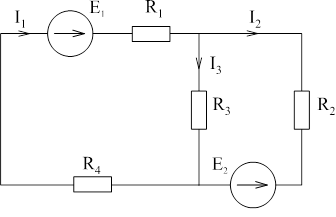
В левой части равенства слагаемое берется со знаком "+" если Е и I совпадают по направлению и со знаком "-" если не совпадают.

Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.

Например:

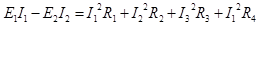
8. Основные понятия переменного тока.

Переменными называют токи и напряжения, изменяющиеся во времени, по величине и направлению. Их величина в любой момент времени называется мгновенным значением. Обозначаются мгновенные значения малыми буквами: i, u, e, p.
Токи, значения которых повторяются через равные промежутки времени, называются периодическими. Наименьший промежуток времени, через который наблюдаются их повторения, называется периодом и обозначается буквой Т. Величина, обратная периоду, называется частотой, т.е.
f=1/T

Максимальное значение переменного тока или напряжения называется амплитудой. Оно обозначается большими буквам с индексом ''m'' (например, Im). Существует также понятие, действующего значения переменного тока (I). Количественно оно равно

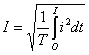
Емкость в цепи синусоидального тока

Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

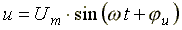
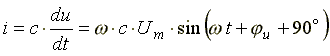(6,13)

Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90^o.

Выражение (6.13) в комплексной форме записи имеет вид:

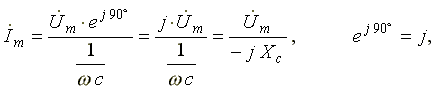(6.14)

где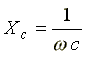- емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

Если комплексное сопротивление индуктивности положительно

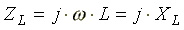, то комплексное сопротивление емкости отрицательно

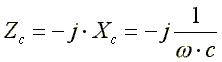
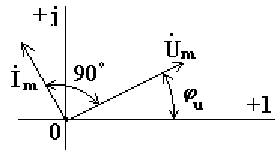
На рис. 6.7 изображена векторная диаграмма цепи с емкостью.
Вектор тока опережает вектор напряжения на 90^o

(6.7)

Треугольник напряжений

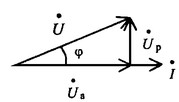
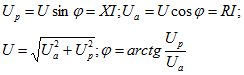
Треугольники токов, сопротивлений и мощностей строятся аналогично

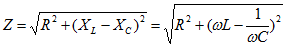
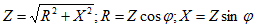
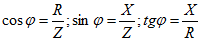
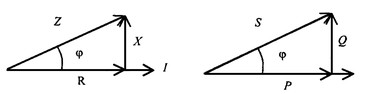
Полная мощность S = UI;
активная мощность
реактивная мощность где

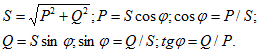
В треугольниках напряжений, токов, сопротивлений и мощностей угол 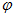сохраняет свое значение.
При параллельном соединении ветвей их проводимости складываются в комплексной форме:

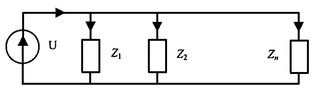
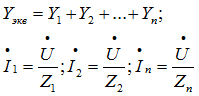
Общий ток, согласно первому закону Кирхгофа:

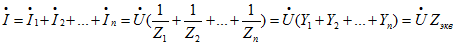
14. Мощности в цепи синусоидального тока. Треугольник мощностей.

http://toe-kgeu.ru/toe1/286-toe1

Определения линейных и фазных величин в трёхфазных цепях.

Основные понятия магнитных цепей.

http://toe-kgeu.ru/toe3/393-toe3

Формулировка закона Ома

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого проводника и обратно пропорциональна его сопротивлению:

I = U / R; [A = В / Ом]

Ом установил, что сопротивление прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.

R = ρl / S,
где ρ - удельное сопротивление, l - длина проводника, S - площадь поперечного сечения проводника.

1. Законы Кирхгофа

1-й закон для узла: Алгебраическая сумма токов в узле равна нулю

2-й закон для контуров:Алгебраическая сумма ЭДС в замкнутом контуре равняется алгебраической сумме падений напряжений на всех участках контура.

8. Энергетический баланс в электрической цепи постоянного тока.

В любой электрической цепи должен соблюдаться энергетический баланс - баланс мощностей: алгебраическая сумма мощностей всех источников равна арифметической сумме мощностей всех приемников энергии.

В левой части равенства слагаемое берется со знаком "+" если Е и I совпадают по направлению и со знаком "-" если не совпадают.

Если направления ЭДС и тока I в источнике противоположны, то физически это означает, что данный источник работает в режиме потребителя.

Например:

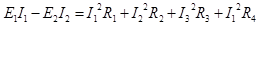
8. Основные понятия переменного тока.

Переменными называют токи и напряжения, изменяющиеся во времени, по величине и направлению. Их величина в любой момент времени называется мгновенным значением. Обозначаются мгновенные значения малыми буквами: i, u, e, p.
Токи, значения которых повторяются через равные промежутки времени, называются периодическими. Наименьший промежуток времени, через который наблюдаются их повторения, называется периодом и обозначается буквой Т. Величина, обратная периоду, называется частотой, т.е.
f=1/T

Максимальное значение переменного тока или напряжения называется амплитудой. Оно обозначается большими буквам с индексом ''m'' (например, Im). Существует также понятие, действующего значения переменного тока (I). Количественно оно равно

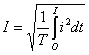
Векторное представление синусоидальных токов и напряжений.

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂ (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами.При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

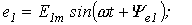
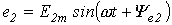
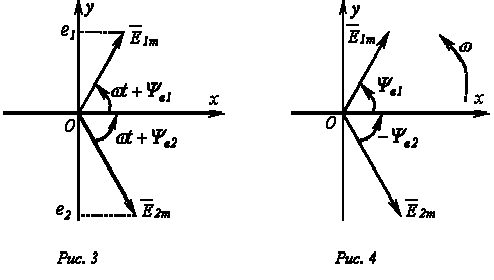
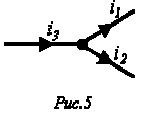Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей: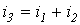

Каждый из этих токов синусоидален и может быть представлен уравнением

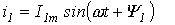и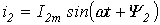
Результирующий ток также будет синусоидален:

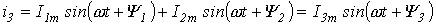
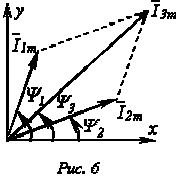
Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов : .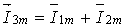

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: 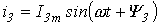.