Частица в одномерной бесконечной прямоугольной яме. Квантование состояний.

Пространственно ограниченное квантовое движение- одномерное движение чатицы, находящейся в силовом поле, энергия взаимодействия с которым имеет вид бесконечно глубокой потенциальной ямы с вертикальными стенками. Находясь внутри ямы, частица движется свободно на участке , а на краях силовое поле возвращает ее обратно в яму.

Потенциальная яма , где - ширина ямы, а энергия отсчитывается от ее дна. Никакая частица не может выйти из этой ямы. Если частица классическая, то на участке она движется с неизменным импульсом и энергией. Достигая стенок ямы, частица испытывает упругий удар и меняет направление на противоположное. Частота таких колебаний частицы зависит от скорости частицы и ширины ямы . В зависимости от скорости, если

1) , то положим равной 0; 2) : частица движется между стенками, и график плотности распределения вероятности будет выглядеть в виде прямой (см. рисунок).

Для реальной частицы: запишем уравнение Шредингера, учитывая что внутри ямы U=0: . За пределы ямы частица не проникает, поэтому волновая функция вне ямы равна 0, следовательно, на границах ямы . С учетом граничных условий волновая функция должна представлять собой стоячую волну. Решение ищем в виде . . . По второму граничному условию: . , где n - квантовое число. Для определения constC используем условие нормировки: , т. к. вероятность обнаружения частицы внутри ямы равна 1, следовательно . Как видно, волновые функции обращаются в ноль на границах ямы. Внутри ямы они представляют собой отрезки синусоиды. Основное условие, котрое должно выполняться,- на ширине ямы должно укладываться целое количество для каждой синусоиды. Количество этих половинок определяется значением целого числа n. Анализ графиков показывает, что вероятность нахождения квантовой частицы в потенциальной яме зависит от координаты x. Так в случае n=1 наибольшая вероятность существует для центра ямы и т.д. Получили, что если у классической частицы плотность вероятности внутри потенциальной ямы всюду одинакова, то у квантовой частицы она является функцией координат. Рассмотрим Е: из граничных условий , то , где , т. е. есть множество значений энергии, которые частица не принимает. Таким образом, энергия дискретна, т. е. квантована. Чем меньше , тем выше ; состояния частицы дискретны. Энергия пробегает ряд значений, не равных 0. Разрешенные энергии частицы называются энергетическими уровнями, они появляются, если частица ограничена в пространстве. Разность энергий двух соседних уровней . С увеличением n соседние уровни удаляются друг от друга. Величина энергетического зазора между уровнями зависит также от массы частицы m и ширины ямы l. Чем меньше эти величины, тем больше расстояние между уровнями. С увеличением ширины ямы или массы частицы уровни сгущаются и их дискретность все менее заметна. В пределе беск широкой ямы или частицы с беск большой массы получаем классический непрерывный спектр энергии.

Изобразим волновую функцию на фоне уравнений при .

- основное состояние (основной энергетический уровень).

У классической частицы этот график выглядит в виде прямой, параллельной оси Ох.

Минимальное значение энергии . Состояние частицы с такой энергией называется основным состоянием. То, что квантовая частица не может иметь энергию, равную нулю согласуется с принципом неопределенности. Волновая функция и энергия состояния квантовой частицы в потенциальной яме однозначно определяются величиной целого числа n, которое определяется квантовым числом системы.

Образование молекул. Ковалентная и ионная связь.

Молекулярные структуры существуют благодаря химическим связям, которые обеспечиваются электронами валентных оболочек.

Связи образуются за счёт частичной или полной передачи валентных электронов.

1. Ковалентная связь

Обусловлена обменом парой электронов с противоположным спином.

Начинаем сближать эти две ямы. Электрон может попадать из одной ямы в другую. В конце концов он перестанет различать эти две ямы и будет принадлежать двум ямам.

ψ₁₂=ψ₁±ψ₂

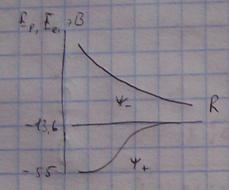
ψ₊=ψ₁+ψ₂

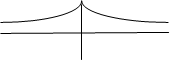
ψ_-=ψ₁-ψ₂

	ψ+

Симметричная функция

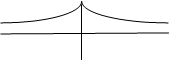Состояние, стягивающее систему.

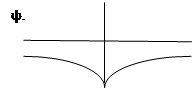Антисимметричная функция

Состояние, разваливающее систему.

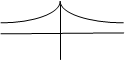
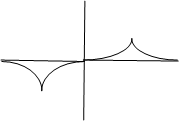
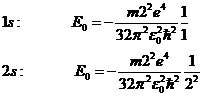
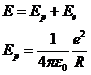
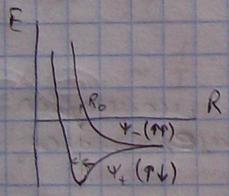F=grad(v)

( ) – направление спинов

Состояние ψ₊ характеризуется minэнергии и является связывающим.

Молекула водорода образуется только в случае, если 2 электрона направлены с разнонаправленными спинами. В противном случае молекула не образуется.

Ковалентная связь является обменным взаимодействием.

Ионная связь.

Для ионной связи характерна полная передача электронов одного атома другому.

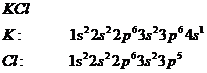
По мере объединения атомов молекулы исходного атомарного уровня расщепляются.

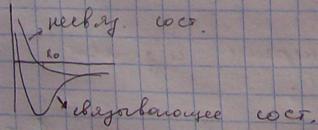
По мере сближения атомов снимается (?) вырождение состояний