Теоремы умножения вероятностей.

Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

Также можно записать:

Доказательство этой теоремы непосредственно вытекает из определения условной вероятности.

Если события независимые, то , и теорема умножения вероятностей принимает вид:

В случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились.

Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события.

Если в результате испытания может появиться п событий, независимых в совокупности, то вероятность появления хотя бы одного из них равна

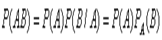
Здесь событие А обозначает наступление хотя бы одного из событий A_i, а q_i – вероятность противоположных событий .

Теорема о вероятности хотя бы одного события.

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий А₁ , А₂ , ..., А_n , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

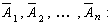
Р (A) = 1 — q₁q₂ ... q_n.(*)

Доказательство

Ч а с т н ы й с л у ч а й. Если события А₁ , А₂ , ..., А_n имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий

P (A) = l — qⁿ. (**)

Формула полной вероятности.

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

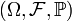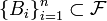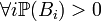
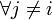
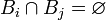
Пусть дано вероятностное пространство , и полная группа попарно несовместных событий , таких что 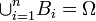. Пусть 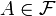— интересующее нас событие. Тогда

.

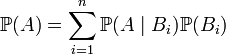Формула полной вероятности также имеет следующую интерпретацию. Пусть 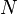— случайная величина, имеющая распределение

.

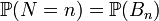Тогда

,

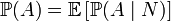т.е. априорная вероятность события равна среднему его апостериорной вероятности.

Теорема Байеса.

Теорема Байеса (или формула Байеса) — одна из основных теорем теории вероятностей, которая позволяет определить вероятность того, что произошло какое-либо событие (гипотеза) при наличии лишь косвенных тому подтверждений (данных), которые могут быть неточны. Названа в честь её автора, преп. Томаса Байеса (посвящённая ей работа «AnEssaytowardssolving a ProblemintheDoctrineofChances» впервые опубликована в 1763 году,[1] через 2 года после смерти автора). Полученную по формуле вероятность можно далее уточнять, принимая во внимание данные новых наблюдений.

Психологические эксперименты[2] показали, что люди при оценках вероятности игнорируют различие априорных вероятностей (ошибка обоснования оценки (англ.)русск.), и потому результаты по формуле Байеса и правильные результаты могут сильно отличаться от ожидаемых.

Формула Байеса:

,

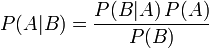где

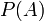— априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

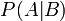— вероятность гипотезы A при наступлении события B (апостериорная вероятность);

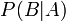— вероятность наступления события B при истинности гипотезы A;

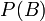— полная вероятность наступления события B.