Одноканальная СМО с ожиданием

Пусть СМО имеет только один канал (n=1), на который поступает пуассоновский поток заявок П_вх с интенсивностью 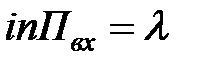. Поток обслуживания простейший и имеет интенсивность m. Заявка, поступившая на вход в момент, когда канал занят обслуживанием не покидает систему, а становится в очередь и ожидает обслуживания. Далее предполагаем, что в данной системе нет ограничений на длину очереди и на время ожидания в очереди. Таким образом, длина очереди станет бесконечной, как и число состояний СМО.

Такая система представляет собой предельный случай системы, при m®¥.

Если l>m, т.е. среднее число заявок, поступивших в систему за единицу времени, больше среднего числа обслуживаемых заявок за то же время при непрерывно работающем канале, то очевидно, что очередь неограниченно растёт. В этом случае предельный режим не устанавливается и предельных вероятностей состояний не существует.

Если l=m, и при условии, что входящий поток заявок П_вх и поток обслуживаний П_об регулярные, то очереди вообще не будет и канал будет обслуживать заявки непрерывно. Но как только или входящий поток заявок П_вх или поток обслуживаний П_об перестаёт быть регулярным и приобретают элементы случайности, очередь начинает расти до бесконечности.

Итак, если l≥m, т.е. СМО с ожиданием без ограничений на очередь перегружена, то есть нагрузка на систему 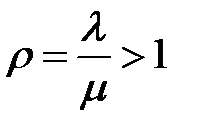, то предельный режим не устанавливается и предельных вероятностей состояний не существует.

Только, если l<m, или нагрузка на систему 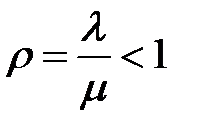, то предельный режим устанавливается и предельные вероятности состояний существуют.

Таблица 8.9 - Параметры одноканальной СМО с ожиданием

№ п/п	Параметры	Обозначения, значения, формулы
1.	Число каналов обслуживания	n=1
2.	Максимальная длина очереди (максимальное число мест в очереди)	m®¥
3.	Интенсивность входящего простейшего потока заявок Пвх	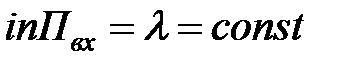, (l не зависит от времени t)
4.	Производительность каждого канала – интенсивность простейшего «потока обслуживаний» Поб (среднее число заявок, обслуживаемое одним каналом за единицу времени при непрерывной его работе без простоя)	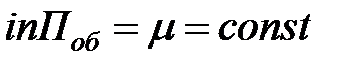, (m не зависит от времени t)
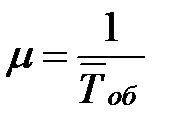5.	Соотношения между l и m	l<m или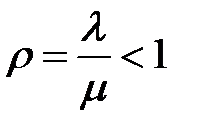

Таблица 8.10 - Предельные характеристики эффективности функционирования одноканальной СМО с ожиданием

№ п/п	Предельные характеристики	Обозначения, формулы
1.	Среднее время обслуживания одной заявки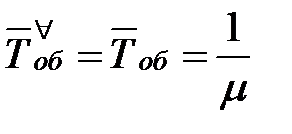
2.	Приведённая интенсивность входящего потока - трафик (показатель нагрузки СМО)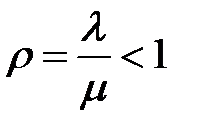
3.	Вероятности состояний СМО рk, k=0, 1, …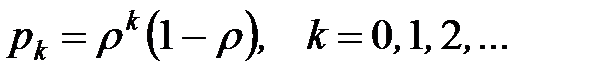
4.	Вероятность отказа ротк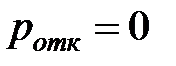
5.	Вероятность того, что поступившая заявка будет принята в систему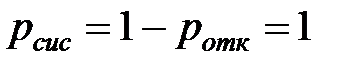
6.	Относительная пропускная способность СМО (средняя доля обслуженных заявок среди поступивших)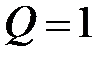
7.	Абсолютная пропускная способность СМО (среднее число обслуживаемых заявок за единицу времени)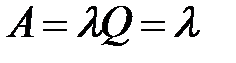
8.	Интенсивность выходящего потока обслуженных заявок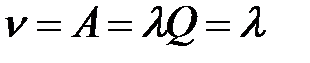

Продолжение таблицы 8.10

№ п/п	Предельные характеристики	Обозначения, формулы
9.	Среднее число заявок в очереди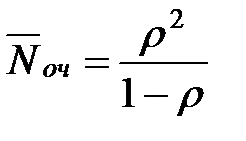
10.	Среднее число заявок под обслуживанием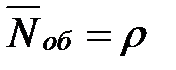
11.	Среднее число заявок в системе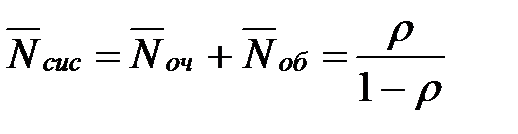
12.	Среднее время ожидания заявки в очереди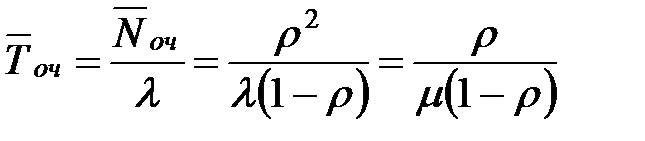
13.	Среднее время пребывания заявки в системе (как в очереди, так и под обслуживанием)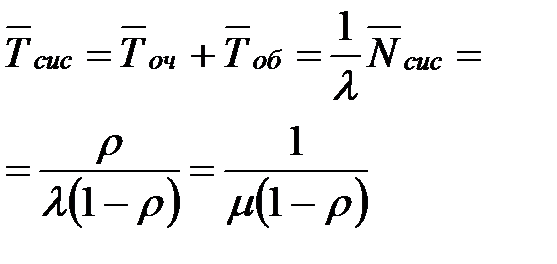

Задача 8.4

Железнодорожную станцию дачного посёлка обслуживает касса с одним окном. В выходные дни, когда население активно пользуется железной дорогой, интенсивность потока пассажиров составляет 0,4 (чел./мин) кассир затрачивает на обслуживание пассажира в среднем 2 мин.

Определить вероятности состояний СМО и основные характеристики эффективности функционирования данной железнодорожной кассы:

· Среднее число пассажиров у кассы;

· Среднее число пассажиров в очереди;

· Среднее время, затрачиваемое пассажиром на приобретение билета;

· Среднее время, ожидания пассажира в очереди.

Решение:

В условиях задачи математической моделью железнодорожной кассы является одноканальная СМО с ожиданием без ограничений на длину очереди и на время ожидания, имеющая своими параметрами:

число каналов n=1;

интенсивность входящего потока 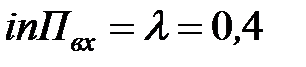(чел./мин);

среднее время обслуживания 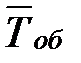=2 мин;

интенсивность потока обслуживаний 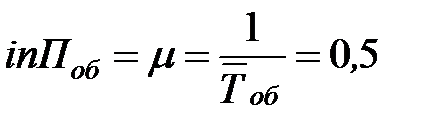(чел./мин);

показатель нагрузки СМО 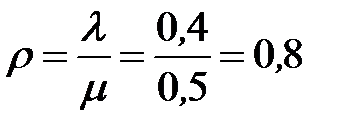(эрланга).

Так как l=0,4<m=0,5, или нагрузка на систему r=0,8<1, то предельный режим устанавливается и предельные вероятности состояний существуют.

Определим вероятности состояний СМО:

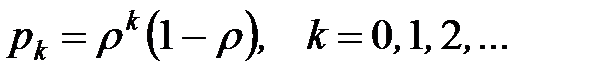
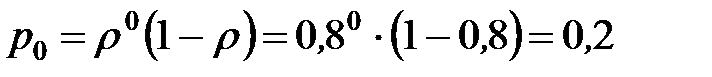- вероятность того, что у кассы нет ни одного человека, или, что кассир свободен;

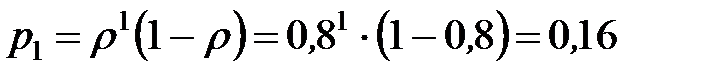- вероятность того, что у кассы один пассажир;

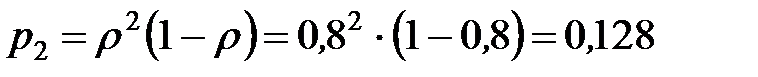- вероятность того, что у кассы два пассажира;

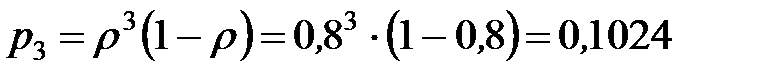- вероятность того, что у кассы три пассажира и т.д.

Определим среднее число заявок в системе:

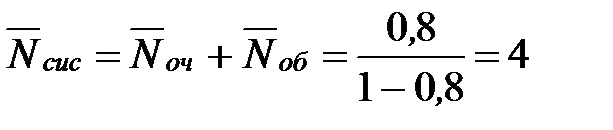- то есть в установившемся предельном режиме среднее число пассажиров у кассы 4 человека – это среднее число пассажиров под обслуживанием и в очереди.

Определим среднее число заявок в очереди:

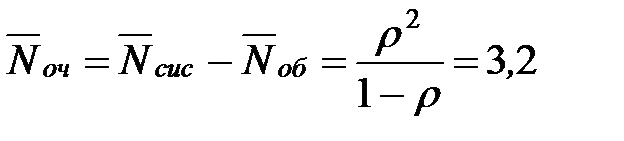- то есть в установившемся предельном режиме среднее число пассажиров находящихся в очереди равно 3 человека.

Определим среднее время пребывания заявки в системе (как в очереди, так и под обслуживанием):

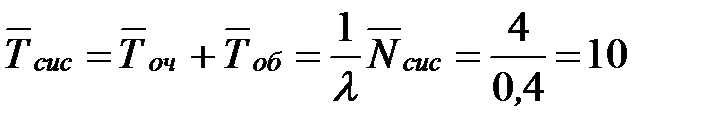- то есть в установившемся предельном режиме среднее время, которое затрачивает пассажир на приобретение билета, складывающееся из среднего времени обслуживания и среднего времени пребывания в очереди составляет 10 минут.

Определим среднее время ожидания заявки в очереди:

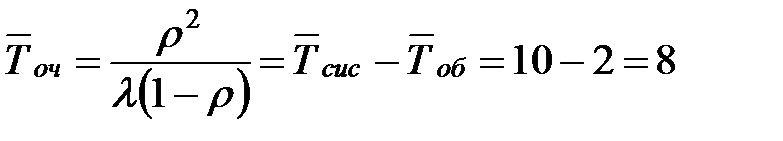- то есть в установившемся предельном режиме среднее время пребывания пассажира в очереди составляет 8 минут, что в четыре раза превышает времени его обслуживания.

Таким образом, чтобы успеть на выбранную электричку, пассажир должен учесть не только время, которое он затрачивает на дорогу до станции, но и подсчитанное время, затрачиваемое на приобретение билета.

Контрольные вопросы

1. Чему равна абсолютная пропускная способность для одноканальной СМО с ожиданием?

2. Чему равна относительная пропускная способность для одноканальной СМО с ожиданием?

3. Что собой представляет среднее число заявок в системе для одноканальной СМО с ожиданием?

4. Чему равна интенсивность выходящего потока заявок для одноканальной СМО с ожиданием?

5. Чему равно среднее число заявок под обслуживанием для одноканальной СМО с ожиданием?

6. Когда существует предельный режим функционирования для одноканальной СМО с ожиданием?

7. Чему равно среднее время пребывания заявки в системе для одноканальной СМО с ожиданием?