Нечёткая логика и нейронные сети
Нечёткая логика и нейронные сети
Введение
Нечёткая логика (англ. fuzzy logic) — раздел математики, являющийся обобщением классической логики и теории множеств, базирующийся на понятии нечёткого множества, впервые введённого Лотфи Заде в 1965 году как объекта с функцией принадлежности элемента к множеству, принимающей любые значения в интервале [0,1] , а не только 0 или 1. На основе этого понятия вводятся различные логические операции над нечёткими множествами и формулируется понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества.
Предметом нечёткой логики считается исследование рассуждений в условиях нечёткости, размытости, сходных с рассуждениями в обычном смысле, и их применение в вычислительных системах.
Направления исследований нечёткой логики
В настоящее время существует, по крайней мере, два основных направления научных исследований в области нечёткой логики:
• нечёткая логика в широком смысле (теория приближенных вычислений);
• нечёткая логика в узком смысле (символическая нечёткая логика).
Символическая нечёткая логика
Символическая нечёткая логика основывается на понятии t-нормы. После выбора некоторой t-нормы (а её можно ввести несколькими разными способами) появляется возможность определить основные операции над пропозициональными переменными: конъюнкцию, дизъюнкцию, импликацию, отрицание и другие.
Нетрудно доказать теорему о том, что дистрибутивность, присутствующая в классической логике, выполняется только в случае, когда в качестве t-нормы выбирается t-норма Гёделя.
Кроме того, в силу определенных причин, в качестве импликации чаще всего выбирают операцию, называемую residium (она, вообще говоря, также зависит от выбора t-нормы).
Определение основных операций, перечисленных выше, приводит к формальному определению базисной нечёткой логики, которая имеет много общего с классической булевозначной логикой (точнее, с исчислением высказываний).
Существуют три основных базисных нечётких логики: логика Лукасевича, логика Гёделя и вероятностная логика (англ. product logic). Интересно, что объединение любых двух из трёх перечисленных выше логик приводит к классической булевозначной логике.
Характеристическая функция
Для пространства рассуждения 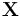 и данной функции принадлежности
и данной функции принадлежности 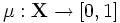 нечёткое множество определяется как
нечёткое множество определяется как
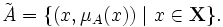
Функция принадлежности 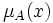 количественно градуирует приналежность элементов фундаментальногомножества пространства рассуждения
количественно градуирует приналежность элементов фундаментальногомножества пространства рассуждения 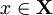 нечёткому множеству
нечёткому множеству 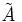 . Значение
. Значение 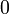 означает, что элемент не включен в нечёткое множество,
означает, что элемент не включен в нечёткое множество, 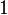 описывает полностью включенный элемент. Значения между
описывает полностью включенный элемент. Значения между 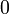 и
и 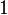 характеризуют нечётко включенные элементы.
характеризуют нечётко включенные элементы.
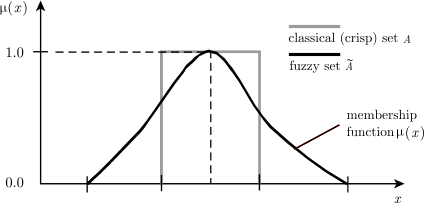
Нечёткое множество и классическое, четкое (crisp) множество
Примеры нечетких множеств
1. Пусть Е = {0, 1, 2, . . ., 10}, М = [0, 1]. Нечеткое множество «Несколько» можно определить следующим образом:
«Несколько» = 0,5/3 + 0,8/4 + 1/5 + 1/6 + 0,8/7 + 0,5/8; его характеристики: высота = 1, носитель = {3, 4, 5, 6, 7, 8}, точки перехода — {3, 8}.
2. Пусть Е = {0, 1, 2, 3,…, n,…}. Нечеткое множество «Малый» можно определить:

3. Пусть Е = {1, 2, 3, . . ., 100} и соответствует понятию «Возраст», тогда нечеткое множество «Молодой» может быть определено с помощью

Нечеткое множество «Молодой» на универсальном множестве Е' = {ИВАНОВ, ПЕТРОВ, СИДОРОВ,...} задается с помощью функции принадлежности μМолодой (x) на Е = {1, 2, 3, . . ., 100} (возраст), называемой по отношению к Е' функцией совместимости, при этом:

где х — возраст СИДОРОВА.
4. Пусть Е = {ЗАПОРОЖЕЦ, ЖИГУЛИ, МЕРСЕДЕС,… } – множество марок автомобилей, а Е' = [0, ∞] — универсальное множество «Стоимость», тогда на Е' мы можем определить нечеткие множества типа:

Рис. 1.1. Примеры функций принадлежности
«Для бедных», «Для среднего класса», «Престижные», с функциями принадлежности вида рис. 1.1.
Имея эти функции и зная стоимости автомобилей из Е в данный момент времени, мы тем самым определим на Е' нечеткие множества с этими же названиями.
Так, например, нечеткое множество «Для бедных», заданное на универсальном множестве Е = { ЗАПОРОЖЕЦ, ЖИГУЛИ, МЕРСЕДЕС,...}, выглядит так, как показано на рис. 1.2.

Рис. 1.2. Пример задания нечеткого множества
Аналогично можно определить нечеткое множество «Скоростные», «Средние», «Тихоходные» и т. д.
5. Пусть Е — множество целых чисел:
Е= {-8, -5, -3, 0, 1, 2, 4, 6, 9}.
Тогда нечеткое подмножество чисел, по абсолютной величине близких к нулю, можно определить, например, так:
А ={0/-8 + 0,5/-5 + 0,6/-3 +1/0 + 0,9/1 + 0,8/2 + 0,6/4 + 0,3/6 + 0/9}.
Логические операции
Включение.Пусть А и В — нечеткие множества на универсальном множестве Е. Говорят, что А содержится в В, если 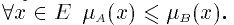
Обозначение: А⊂ В.
Иногда используют термин доминирование, т.е. в случае, когда А⊂ В,говорят, что В доминирует А.
Равенство.А и В равны, если 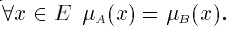
Обозначение: А = В.
Дополнение.Пусть М = [0, 1], А и В – нечеткие множества, заданные на Е. А и В дополняют друг друга, если 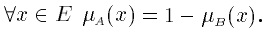
Обозначение: 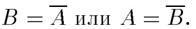
Очевидно, что 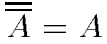 (дополнение определено для М = [0, 1], но очевидно, что его можно определить для любого упорядоченногоМ).
(дополнение определено для М = [0, 1], но очевидно, что его можно определить для любого упорядоченногоМ).
Пересечение. А ⋂ В— наибольшее нечеткое подмножество, содержащееся одновременно в Аи В:
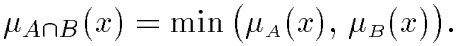
Объединение.A∪В — наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:
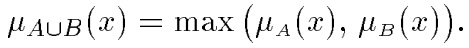
Разность. 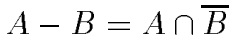 с функцией принадлежности:
с функцией принадлежности:
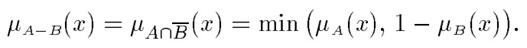
Дизъюнктивная сумма
А⊕ В = (A - B) ∪ (B - A) = (A ⋂ ̅B) ∪ ( ̅A ⋂ B)
с функцией принадлежности:
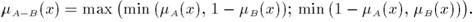
Примеры.Пусть
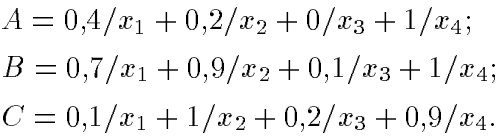
Здесь:
1) А ⊂ В, т. е. А содержится в B или Bдоминирует А С несравнимони с A, ни с В, т.е. пары {А, С} и {А, С} — пары недоминируемых нечетких множеств.
2) A≠ B ≠ C
3) ̅A = 0,6/x1 + 0,8/x2 + 1/x3 + 0/x4; ̅B = 0,3/x1 + 0,1/x2 + 0,9/x3 +0/x4.
4) А ⋂ В = 0,4/x1+ 0,2/x2+ 0/x3+ 1/х4.
5) A ∪ В = 0,7/x1+ 0,9/x2+ 0,1/x3+ 1/x4.
6) А - В = А⋂ ̅В =0,3/x1+ 0,l/x2+ 0/x3+ 0/x4;
В- А= ̅А⋂ В=0,6/x1+ 0,8/x2+ 0,l/x3+ 0/x4.
7) А ⊕ В = 0,6/x1+ 0,8/x2+ 0,1/x3+ 0/x4.
Наглядное представление логических операций над нечеткими множествами. Для нечетких множеств можно строить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значения μА(х), на оси абсцисс в произвольном порядке расположены элементы Е (мы уже использовали такое представление в примерах нечетких множеств). Если Е по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые логические операции над нечеткими множествами (см. рис. 1.3).
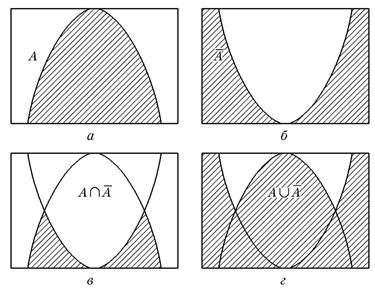
Рис. 1.3. Графическая интерпретация логических операций:
α— нечеткое множество А; б — нечеткое множество̅А, в — А⋂ ̅А; г—A ∪ ̅А
На рис. 1.3α заштрихованная часть соответствует нечеткому множеству А и, если говорить точно, изображает область значений А и всех нечетких множеств, содержащихся в А. На рис. 1.3б, в, гданы ̅А, А ⋂ ̅A,A U ̅А.
Свойства операций∪ и⋂
Пусть А, В, С — нечеткие множества, тогда выполняются следующие свойства:
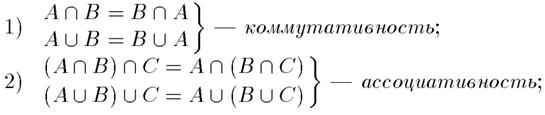

В отличие от четких множеств, для нечетких множеств в общем
случае:
A⋂̅A ≠∅, A ∪ ̅A ≠ E
(что, в частности, проиллюстрировано выше в примере наглядного представления нечетких множеств).
Замечание. Введенные выше операции над нечеткими множествами основаны на использовании операций maxи min. В теории нечетких множеств разрабатываются вопросы построения обобщенных, параметризованных операторов пересечения, объединения и дополнения, позволяющих учесть разнообразные смысловые оттенки соответствующих им связок «и», «или», «не».
Треугольные нормы и конормы
Один из подходов к операторам пересечения и объединения заключается в их определении в классе треугольных норм и конорм.
Треугольной нормой(t-нормой) называется бинарная операция (двуместная действительная функция)
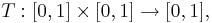
удовлетворяющая следующим условиям:
1. Ограниченность: 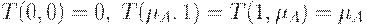 .
.
2. Монотонность: 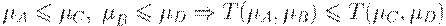 .
.
3. Коммутативность: 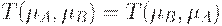 .
.
4. Ассоциативность: 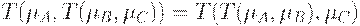 .
.
Примеры треугольных норм
min(μA,μB)
произведение μA·μB
max(0, μA+μB - 1).
Треугольной конормой (сокращенно 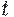 -конормой) называется двухместная действительная функция
-конормой) называется двухместная действительная функция
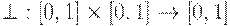 ,
,
удовлетворяющая следующим условиям:
1. Ограниченность: 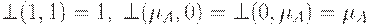 .
.
2. Монотонность: 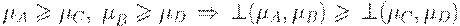 .
.
3. Коммутативность:  .
.
4. Ассоциативность:  .
.
Треугольная конорма 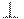 является архимедовой, если она непрерывна
является архимедовой, если она непрерывна
и для любого нечеткого множества 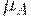 выполнено неравенство
выполнено неравенство 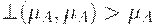 .
.
Она называется строгой, если функция 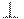 строго убывает по обоим аргументам.
строго убывает по обоим аргументам.
Примеры t-конорм
max(μA,μB)
μA+μB-μA·μB
min(1, μA+μB).
Примерами треугольных конорм являются следующие операторы:
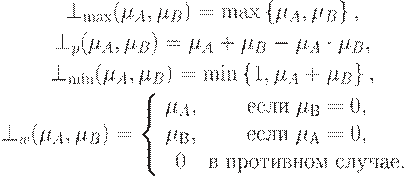
Треугольная норма T и треугольная конорма S называются дополнительными бинарными операциями, если
T(a,b) + S(1 − a,1 − b) = 1
для 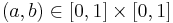 .
.
Наибольшей популярностью в теории Заде пользуются три пары дополнительных треугольных норм и конорм.
1) Пересечение и объединение по Заде:
TZ(a,b) = min{a,b}, SZ(a,b) = max{a,b}.
2) Пересечение и объединение по Лукасевичу:
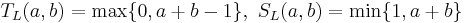 .
.
3) Вероятностное пересечение и объединение:
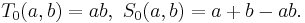
Операторы дополнения
В теории нечетких множеств оператор дополнения не является единственным.
Помимо общеизвестного
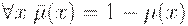 ,
,
существует целый набор операторов дополнения нечеткого множества.
Пусть задано некоторое отображение
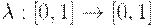 .
.
Это отображение будет называться оператором отрицания в теории нечетких множеств, если выполняются следующие условия:
(1) 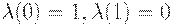
(2) 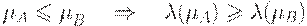
Если кроме этого выполняются условия:
(3) 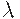 — строго убывающая функция
— строго убывающая функция
(4) 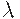 — непрерывная функция
— непрерывная функция
то она называется строгим отрицанием.
Функция 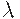 называется сильным отрицанием или инволюцией, если наряду с условиями (1) и (2) для нее справедливо:
называется сильным отрицанием или инволюцией, если наряду с условиями (1) и (2) для нее справедливо:
(5) 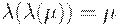 .
.
Приведем примеры функции отрицания:
Классическое отрицание: 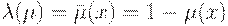 .
.
Квадратичное отрицание: 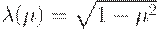 .
.
Отрицание Сугено: 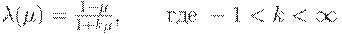 .
.
Дополнение порогового типа: 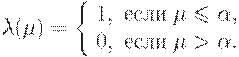 .
.
Будем называть любое значение 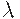 , для которого
, для которого 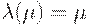 , равновесной точкой. Для любого непрерывного отрицания существует единственная равновесная точка.
, равновесной точкой. Для любого непрерывного отрицания существует единственная равновесная точка.
Нечеткие числа
Нечеткие числа— нечеткие переменные, определенные на числовой оси, т.е. нечеткое число определяется как нечеткое множество А на множестве действительных чисел ℝ с функцией принадлежности μА(х) ϵ [0, 1], где х — действительное число, т.е. х ϵ ℝ.
Нечеткое число А нормально, если тах μА(x) = 1; выпуклое, если для любых х ≤у ≤ z выполняется
μА(х)≥ μА(у) ˄ μA(z).
Множество α-уровня нечеткого числа А определяется как
Аα= {x/μα(x) ≥ α}.
Подмножество SA⊂ ℝ называется носителем нечеткого числа А, если
SA={ x/μA(x)> 0 }.
Нечеткое число А унимодально, если условие μА(х) = 1 справедливо только для одной точки действительной оси.
Выпуклое нечеткое число А называется нечетким нулем, если
μА(0) = sup (μA(x)).
Нечеткое число А положительно, если ∀x ϵ SA, х> 0 и отрицательно, если ∀х ϵ SA, х< 0.
Нечеткие числа (L-R)-Tипа
Нечеткие числа (L-R)-типа — это разновидность нечетких чисел специального вида, т.е. задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними.
Функции принадлежности нечетких чисел (L-R)-типa задаются с помощью невозрастающих на множестве неотрицательных действительных чисел функций действительного переменного L(x) и R(x), удовлетворяющих свойствам:
а) L(-x) = L(x), R(-x) = R(x);
б) L(0) = R(0).
Очевидно, что к классу (L-R)-функций относятся функции, графики которых имеют вид, приведенный на рис. 1.7.

Рис. 1.7. Возможный вид (L-R)-функций
Примерами аналитического задания (L-R)-функций могут быть

и т. д.
Пусть L(у)и R(у)— функции (L-R)-типа (конкретные). Унимодальное нечеткое число А с модой а (т. е. μА(а) = 1) с помощью L(у)и R(у) задается следующим образом:

где а — мода; α > 0, β > 0 — левый и правый коэффициенты нечеткости.
Таким образом, при заданных L(у)и R(у) нечеткое число (унимодальное) задается тройкой А = (а, α, β).
Толерантное нечеткое число задается, соответственно, четверкой параметров А = (a1, а2, α, β), где а1 иа2 — границы толерантности, т.е. в промежутке [a1, а2] значение функции принадлежности равно 1.
Примеры графиков функций принадлежности нечетких чисел (L-R)-типа приведены на рис. 1.8.

Рис. 1.8. Примеры графиков функций принадлежности нечетких чисел (L-R)-типа
Отметим, что в конкретных ситуациях функции L(у),R(у),а также параметры а, β нечетких чисел (а, α, β) и (a1, а2, α, β) должны подбираться таким образом, чтобы результат операции (сложения, вычитания, деления и т.д.) был точно или приблизительно равен нечеткому числу с теми же L(у)и R(у),а параметры α' и β'результата не выходили за рамки ограничений на эти параметры для исходных нечетких чисел, особенно если результат в дальнейшем будет участвовать в операциях.
Замечание. Решение задач математического моделирования сложных систем с применением аппарата нечетких множеств требует выполнения большого объема операций над разного рода лингвистическими и другими нечеткими переменными. Для удобства исполнения операций, а также для ввода-вывода и хранения данных, желательно работать с функциями принадлежности стандартного вида.
Нечеткие множества, которыми приходится оперировать в большинстве задач, являются, как правило, унимодальными и нормальными. Одним из возможных методов аппроксимации унимодальных нечетких множеств является аппроксимация с помощью функций (L-R)-типа.
Примеры (L-R)-представлений некоторых лингвистических переменных приведены в табл. 1.2.
Таблица 1.2. Возможное (L-R)-представление некоторых лингвистических переменных

Нечеткие отношения
Нечеткие отношения играют фундаментальную роль в теории нечетких систем. Аппарат теории нечетких отношений используется при построении теории нечетких автоматов, при моделировании структуры сложных систем, при анализе процессов принятия решений.
Основные определения
Теория нечетких отношений находит также приложение в задачах, в которых традиционно применяется теория обычных (четких) отношений. Как правило, аппарат теории четких отношений используется при качественном анализе взаимосвязей между объектами исследуемой системы, когда связи носят дихотомический характер и могут быть проинтерпретированы в терминах "связь присутствует", "связь отсутствует", либо когда методы количественного анализа взаимосвязей по каким-либо причинам неприменимы и взаимосвязи искусственно приводятся к дихотомическому виду. Например, когда величина связи между объектами принимает значения из ранговой шкалы, выбор порога на силу связи позволяет преобразовать связь к требуемому виду. Однако, подобный подход, позволяя проводить качественный анализ систем, приводит к потере информации о силе связей между объектами либо требует проведения вычислений при разных порогах на силу связей. Этого недостатка лишены методы анализа данных, основанные на теории нечетких отношений, которые позволяют проводить качественный анализ систем с учетом различия в силе связей между объектами системы.
Обычное неразмытое 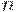 -арное отношение
-арное отношение 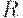 определяется как подмножество декартова произведения
определяется как подмножество декартова произведения 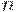 множеств
множеств

Подобно нечеткому множеству, нечеткое отношение можно задать с помощью его функции принадлежности

где в общем случае будем считать, что  — это полная дистрибутивная решетка. Таким образом,
— это полная дистрибутивная решетка. Таким образом,  — это частично упорядоченное множество, в котором любое непустое подмножество имеет наибольшую нижнюю и наименьшую верхнюю грани иоперации пересечения и объединения в
— это частично упорядоченное множество, в котором любое непустое подмножество имеет наибольшую нижнюю и наименьшую верхнюю грани иоперации пересечения и объединения в  удовлетворяют законам дистрибутивности. Все операции над нечеткими отношениями определяются с помощью этих операций из
удовлетворяют законам дистрибутивности. Все операции над нечеткими отношениями определяются с помощью этих операций из  . Например, если в качестве
. Например, если в качестве  взять ограниченное множество вещественных чисел, то операциями пересечения и объединения в
взять ограниченное множество вещественных чисел, то операциями пересечения и объединения в  будут, соответственно, операции
будут, соответственно, операции  и
и  , и этиоперации будут определять и операции над нечеткими отношениями.
, и этиоперации будут определять и операции над нечеткими отношениями.
Далее мы ограничимся рассмотрением лишь бинарных нечетких отношений, являющихся отображением на отрезок  , т.е.
, т.е.  .
.
Если множества  и
и  конечны, нечеткое отношение
конечны, нечеткое отношение 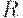 между
между  и
и  можно представить с помощью его матрицы отношения, первой строке и первому столбцу которой ставятся в соответствие элементы множеств
можно представить с помощью его матрицы отношения, первой строке и первому столбцу которой ставятся в соответствие элементы множеств  и
и  , а на пересечении строки
, а на пересечении строки  и столбца
и столбца  помещается элемент
помещается элемент  (см. табл.2.1).
(см. табл.2.1).
| Таблица 2.1. | ||||
 |  |  |  | |
 | 0,5 | 0,8 | ||
 | 0,7 | 0,6 | 0,3 | |
 | 0,7 | 0,4 |
В случае, когда множества  и
и  совпадают, нечеткое отношение
совпадают, нечеткое отношение 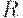 называют нечетким отношением на множестве X.
называют нечетким отношением на множестве X.
В случае конечных или счетных универсальных множеств очевидна интерпретация нечеткого отношения в виде взвешенного графа, в котором каждая пара вершин  из
из  соединяется ребром с весом
соединяется ребром с весом  .
.
Пример. Пусть  и
и  , тогда нечеткий граф, изображенный на рис рис. 2.1, задает некотороенечеткое отношение
, тогда нечеткий граф, изображенный на рис рис. 2.1, задает некотороенечеткое отношение  .
.

Рис. 2.1.
Свойства нечетких отношений
Различные типы нечетких отношений определяются с помощью свойств, аналогичных свойствам обычных отношений, причем для нечетких отношений можно указать различные способы обобщения этих свойств.
1. Рефлексивность:

2. Слабая рефлексивность:

3. Сильная рефлексивность:

4. Антирефлексивность:

5. Слабая антирефлексивность:

6. Сильная антирефлексивность:

7. Симметричность:

8. Антисимметричность:

9. Асимметричность:

10. Сильная линейность:

11. Слабая линейность:

12. Транзитивность:

Проекции нечетких отношений
Важную роль в теории нечетких множеств играет понятие проекции нечеткого отношения. Дадим определение проекции бинарного нечеткого отношения.
Пусть 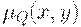 — функция принадлежности нечеткого отношения в
— функция принадлежности нечеткого отношения в 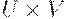 . Проекции
. Проекции 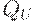 и
и 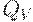 отношения
отношения 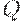 на
на 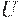 и
и 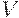 — есть множества в
— есть множества в 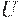 и
и  с функцией принадлежности вида
с функцией принадлежности вида
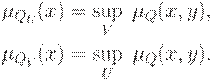
Условной проекцией нечеткого отношения 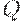 на
на 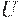 , при произвольном фиксированном
, при произвольном фиксированном  , называется множество
, называется множество 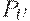 с функцией принадлежности вида
с функцией принадлежности вида  .
.
Аналогично определяется условная проекция на 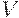 при заданном
при заданном 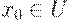 :
:

Из данного определения видно, что проекции 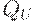 и
и 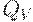 не влияют на условные проекции
не влияют на условные проекции 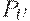 и
и 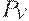 , соответственно. Дадим далее определение, которое учитывает их взаимосвязь.
, соответственно. Дадим далее определение, которое учитывает их взаимосвязь.
Условные проекции второго типа определяются следующим образом:
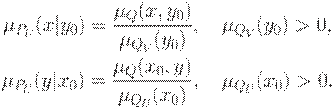
Если 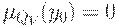 или
или 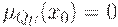 , то полагаем, соответственно, что
, то полагаем, соответственно, что 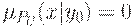 или
или 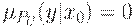 .
.
Заметим, что условные проекции первого типа содержатся в соответствующих проекциях второго типа.
Пусть 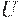 и
и 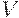 — базовые множества,
— базовые множества, 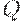 — нечеткое отношение в
— нечеткое отношение в 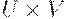 и
и 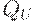 и
и 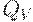 — его проекции на
— его проекции на 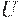 и
и 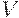 , соответственно.
, соответственно.
Нечеткие множества 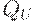 и
и 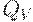 называются независимыми, если
называются независимыми, если
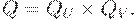
Следовательно, они независимы по первому типу, если
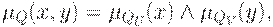
и независимы по второму типу, если
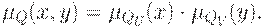
В противном случае проекции 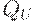 и
и 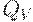 являются зависимыми (соответствующего типа).
являются зависимыми (соответствующего типа).
Независимость второго типа можно интерпретировать следующим образом. Данные соотношения с учетом произвольности 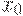 и
и 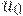 перепишем в виде
перепишем в виде
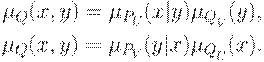
Классы нечетких отношений
Аннотация: В лекции приводится классификация нечетких отношений, рассматриваются классы нечетких отношений сходства и различия, а также класс нечетких порядков. В качестве примеров применения теории нечетких отношений рассматриваются задачи нечеткой классификации и нечеткого упорядочения.
Все типы нечетких отношений в зависимости от свойств, которыми они обладают, могут быть разделены на три больших класса.
В первый класс входят симметричные отношения, которые обычно характеризуют сходство или различие между объектами множества  .
.
Второй класс образуют антисимметричные отношения; они задают на множестве  отношения упорядоченности, доминирования, подчиненности и т.п.
отношения упорядоченности, доминирования, подчиненности и т.п.
Третий класс состоит из всех остальных отношений.
Отношения каждого класса, в свою очередь, могут быть разделены на подклассы в зависимости от выполнения условий рефлексивности и антирефлексивности.
Рефлексивные и симметричные отношения обычно называют отношениями сходства, толерантности, безразличия или неразличимости. В дальнейшем эти отношения будем называть отношениями сходства и обозначать буквой 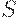 .
.
Антирефлексивные и симметричные отношения называютсяотношениями различияи обозначаются буквой 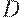 .
.
Отношения сходства и отношения различиядвойственны друг другу.
Антисимметричные отношения, называемые предпорядками и обозначаемые буквой 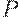 , в зависимости от выполнения условия рефлексивности или антирефлексивности делятся на нестрогие и строгие порядки.
, в зависимости от выполнения условия рефлексивности или антирефлексивности делятся на нестрогие и строгие порядки.
Из отношений третьего класса, обозначаемых буквой 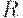 , обычно выделяют лишь рефлексивные отношения, которые будут называться слабыми порядками.
, обычно выделяют лишь рефлексивные отношения, которые будут называться слабыми порядками.
На следующем уровне классификации из каждого класса отношений могут быть выделены отношения специального вида. Определяющим условием для них является условие транзитивности. Оно устанавливает связь между силой отношения для различных пар объектов из  .
.
Эта связь может быть очень слабой, а может накладывать достаточно сильные ограничения на возможные значения силы отношения между объектами из  . Число отличающихся друг от друга условий транзитивности зависит от типа отношения, для которого они формулируются.
. Число отличающихся друг от друга условий транзитивности зависит от типа отношения, для которого они формулируются.
Условия транзитивности зависят от вида операций, с помощью которых они определяются. Наиболее общими условиями транзитивности являются условия, определяемые с помощью решеточных операций 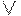 и
и 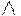 в
в  . Более частыми являются условия, определяемые с помощью дополнительных операций в
. Более частыми являются условия, определяемые с помощью дополнительных операций в  и зависящих от конкретного вида
и зависящих от конкретного вида  . В этих случаях указывается вид соответствующего множества
. В этих случаях указывается вид соответствующего множества  . Далее мы будем рассматривать нечеткие отношения, определенные на множестве
. Далее мы будем рассматривать нечеткие отношения, определенные на множестве 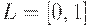 .
.
Порядки и слабые порядки
Антисимметричное, транзитивное нечеткое отношение 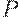 называется отношением упорядочения или порядком. Мы будем рассматривать только строгие порядки, т.е. порядки, для которых выполняется свойство антирефлексивности. Свойства нестрогих (рефлексивных)порядков во многом совпадают со свойствами строгих порядков.
называется отношением упорядочения или порядком. Мы будем рассматривать только строгие порядки, т.е. порядки, для которых выполняется свойство антирефлексивности. Свойства нестрогих (рефлексивных)порядков во многом совпадают со свойствами строгих порядков.
Различные порядки отличаются друг от друга требованиями, предъявляемыми к условию транзитивности. Слабейшее из этих требований — условие ацикличности отношения строгого порядка 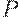 , наиболее жесткие требования — условия линейной транзитивности и условие квазисерийности.
, наиболее жесткие требования — условия линейной транзитивности и условие квазисерийности.
Если для отношения сходства условие транзитивности обычно записывают в виде  и различные способы определения операции композиции позволяют задавать разные типы транзитивности, причем оказывается, что таких типов существует не так уж и много, то для отношения порядка условие транзитивности нечеткого отношения удобно записывать в виде, аналогичном условию транзитивности обычных порядков:
и различные способы определения операции композиции позволяют задавать разные типы транзитивности, причем оказывается, что таких типов существует не так уж и много, то для отношения порядка условие транзитивности нечеткого отношения удобно записывать в виде, аналогичном условию транзитивности обычных порядков:

где  — некоторая операция в
— некоторая операция в  . Оказывается, что из множества всех отношений порядка можно выделить значительное количество отличающихся друг от друга классов порядков специального вида, определяемых как способом задания операции
. Оказывается, что из множества всех отношений порядка можно выделить значительное количество отличающихся друг от друга классов порядков специального вида, определяемых как способом задания операции  в
в  , так и способом записи условия транзитивности. Далее перечислим некоторые условия транзитивности, определяющие эти классы нечетких строгих порядков. Учитывая асимметричность отношения строгого порядка
, так и способом записи условия транзитивности. Далее перечислим некоторые условия транзитивности, определяющие эти классы нечетких строгих порядков. Учитывая асимметричность отношения строгого порядка 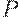 , будем полагать
, будем полагать  , если
, если  .
.
Ацикличность:

Слабая транзитивность:

Отрицательная транзитивность:

( 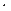 )- транзитивность:
)- транзитивность:

