Линейная акустика идеальной среды
Исходя из основных уравнений гидродинамики (см. главу 1), получим уравнение для звуковых волн малой амплитуды в идеальной среде.
Для этого запишем уравнение непрерывности
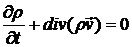 (9.1)
(9.1)
и уравнение Эйлера
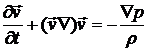 , (9.2)
, (9.2)
где р - давление, ρ -плотность, 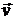 - скорость частицы.
- скорость частицы.
Представим переменные р и ρ в виде:
р = p0+ р' , ρ = ρ0 + ρ' , (9.3)
где p0, ρ0 — постоянные равновесные давление и плотность, р', ρ' - их изменения в звуковой волне ( р' « p0 , ρ' « ρ0 ).
Подставляя (9.3) в (9.1) и (9.2) и пренебрегая малыми величинами второго порядка относительно р', ρ' и скорости 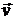 , получим линеаризованные уравнения для акустических величин:
, получим линеаризованные уравнения для акустических величин:
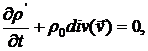 (9.4)
(9.4)
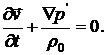 (9.5)
(9.5)
Звуковая волна в идеальной жидкости есть адиабатическое движение. При этом давление р зависит только от одной термодинамической величины, например от плотности ρ (баротропная среда): р = р (ρ). Поэтому
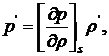 (9.6)
(9.6)
где s - энтропия. Тогда из (9.4) получим
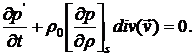 (9.7)
(9.7)
Введем потенциал скорости φ :



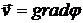 . (9.8)
. (9.8)
Из уравнения (9.5) имеем
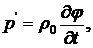 (9.9)
(9.9)
а из (9.7) - (9.9) находим волновое уравнение для потенциала φ:
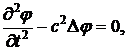 (9.10)
(9.10)
в котором Δ - оператор Лапласа, с - скорость звука,
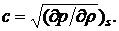 (9.11)
(9.11)
В случае плоской волны, распространяющейся по оси х, уравнение (9.10)
принимает вид:
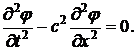 (9.12)
(9.12)
Заметим, что условие применимости линеаризованных уравнений движения р' « p0 , ρ' « ρ0 эквивалентно малости скорости движения частиц жидкости в волне по сравнению со скоростью звука: v « с , т.е. малости числа Маха (М = v/c « 1).
Найдем решение волнового уравнения для бегущей плоской волны и покажем, что звуковая волна является продольной.
Уравнение (9.12) имеет общее решение
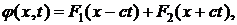
где F1 и F2 - произвольные функции. Рассматривая, например, волну, распространяющуюся в положительном направлении оси х, для потенциала скорости 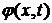 имеем
имеем
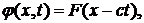 (9.13)
(9.13)
и, следовательно, картина возмущений распространяется в среде со скоростью с, называемой скоростью звука. Из формул (9.13) и (9.8) видно, что в бегущей волне колебательная скорость имеет единственную компоненту vx = v. Это означает, что частицы среды в волне колеблются вдоль направления ее распространения, т.е. звуковая волна является продольной. При этом колебательная скорость v связана с приращениями давления р' и плотности ρ' простыми алгебраическими соотношениями.
Используя формулы (9.8) и (9.9), из (9.13) получаем
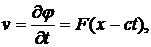
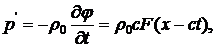 (9.14)
(9.14)
и, следовательно,
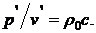 (9.15)
(9.15)
Соотношение (9.15) иногда называют акустическим законом Ома, а величину ρ0с - волновым сопротивлением.
Используя линеаризованное уравнение состояния (9.6), для возмущений плотности ρ ' и колебательной скорости имеем
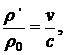 (9.16)
(9.16)
Градиент акустического давления, как видно из формулы (9.5), коллинеарен вектору колебательной скорости и в силу продольного характера звуковой волны -направлению на источник звука. Таким образом, используя приемники градиента давления, можно определить направление прихода акустической волны.
Рассмотрим решение волнового уравнения для плоской монохроматической волны и определим соотношения между амплитудами давления и смещения, колебательной скорости и ускорения частиц. Решение волнового уравнения для давления в гармонической волне можно записать в виде
p'(x,t) = p'o cos (wt-kx), (9.28)
где p'o - амплитуда давления, w - частота, k = w /c —волновое число. Из (9.15) следует, что колебательная скорость находится в фазе с давлением
v(x,t) = vo cos (wt-kx), vo = p'o /( 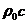 ) (9.29)
) (9.29)
Для амплитуды смещения частиц 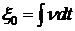 и ускорения
и ускорения 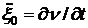 имеем
имеем

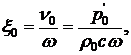
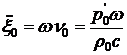 .
.  (9.30)
(9.30)
Часто используется эффективное среднеквадратичное давление рэф, определяемое через среднее от квадрата звукового давления за один период волны Т = 2π/ω:
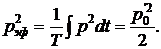
Следовательно,
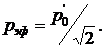
Для объемной плотности энергии и интенсивности (силы звука) плоской звуковой волны получим следующие выражения
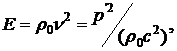
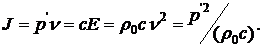 (9.31)
(9.31)
В гармонической волне (9.28) средняя за период сила звука равна
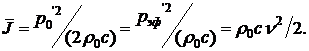 (9.32)
(9.32)
Примеры решения задач
1. В атмосферной акустике принято характеризовать уровень интенсивности В = 10 lg (J/Jст) относительно стандартного нулевого уровня с интенсивностью Jст =10-12 Вт/м2 . Чему равняется среднее звуковое давление рст в воздухе при нормальных условиях (атмосферное давление 105 Па, t = 0 °С) волны нулевой интенсивности (с = 332 м/с, ρ0 = 1,26 кг/м3)? Записать выражение для уровня звукового давления относительно стандартного давления рст.
Решение. Для эффективного звукового давления получаем
рст = ( Jст ρ0с)1/2 ≈ 2,04•10-5 Па.
Уровень звука при этом записывается как
В = 10 lg (J/Jст) = 20 lg (p/pст).
2. Амплитуда звукового давления р'0 = 0,1 Па. Найти уровень интенсивности в воздухе при температуре 20 °С и давлении 1 атм.
Решение. Используя определения
В = 10 lg (J/Jст ), J = p'02/(2ρ0с) , Jст =10-12 Вт/м2,
и подставляя значения ρ0 и c при t = 20 °С (ρ0 = 1,29 кг/м3 и с = 340 м/с), имеем J= 1,14•10-5 Вт/м2 . Следовательно, В = 70,6 дБ.
3. В гидроакустике уровень звукового давления принято отсчитывать относительно давления рн = 1 мкПа = 10-6 Па, Вн = 20 lg (p/pн). Найти формулу пересчета от Вн к стандартному уровню интенсивности Jст =10-12 Вт/м2, соответствующему в воде (ρ0= 103 кг/м3, с = 1500 м/с) эффективному давлению рэф.
Решение. Найдем значение стандартного нулевого уровня:
Jст = pэф2/(ρ0с).
Отсюда рэф =1,22•10-3 Па. Следовательно,
Вн = 20 lg(p/10-6), В = 20 lg[p/( 1,22•10-3)],
из которых получаем
Вн = В - 61,72.
4. Найти условие, при котором распространение звуковой волны можно рассматривать как адиабатический процесс.
Решение. Распространение звуковой волны сопровождается изменением температуры. Температура увеличивается в тех областях, где среда подвергается адиабатическому сжатию, и уменьшается в областях адиабатического разрежения. Процесс распространения звука можно считать адиабатическим, если за время, равное периоду звуковой волны, тепло не успеет диффундировать на расстояния порядка длины волны λ. Иными словами, "длина температурной волны" λT (масштаб диффузии, соответствующий частоте f) должна быть малой по сравнению с длиной акустической волны λ = с/f.
Длина температурной волны 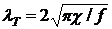 находится из уравнения теплопроводности
находится из уравнения теплопроводности
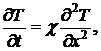
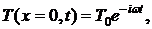
решение которого при х > 0 имеет вид:
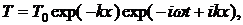
где k = 2π/λT_, χ - коэффициент температуропроводности.
Условие адиабатичности λ > λT будет выполнено для частот
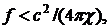
Оценки показывают, что это условие хорошо выполняется в жидкостях и газах, вплоть до очень высоких частот. Так, в воздухе (числовые значения параметров χ= 2,8•10-5 м2/с, с = 330 м/с) звук распространяется адиабатически при частотах f ≤ 1012 Гц.
5. Выразить адиабатический модуль объемной упругости Κa , связывающий приращения давления и плотности
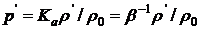
через скорость звука с. Здесь где βa - адиабатический коэффициент сжатия.
Решение. Согласно (9.6), малые возмущения давления и плотности в звуковой волне связаны соотношением
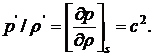
Из формул задачи (9.10) получаем
Ka=ρ0c2.
Таким образом, измеряя скорость звука и плотность среды, можно найти ее объемный модуль упругости. Такой способ оказывается наиболее эффективным для слабо сжимаемых сред - жидкостей и твердых тел. Заметим, что число Маха М = v/c может быть также записано как
М = p'/ρ0 = р'/Kа..
Поэтому величину Ka иногда называют характерным внутренним давлением среды.
6. Вывести формулу для скорости звука в идеальном газе.
Решение. Уравнение адиабатического процесса в идеальном газе имеет вид
p/ργ = const = p0/ρ0γ,
где p0 , ρ0 - равновесные значения давления и плотности, γ = сp /сv —показатель адиабаты, равный отношению теплоемкостей газа при постоянном давлении и постоянном объеме.
Для того чтобы найти (∂р/∂ρ)s , представим плотность и давление в виде (9.3). Тогда, линеаризуя предыдущее выражение, получаем
p ’= (γp0/ρ0)ρ’ .
Используя уравнение состояния идеального газа, имеем
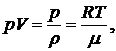
где R = 8,314 Дж/(моль*К) - универсальная газовая постоянная, μ - молекулярная масса, T - температура в Кельвинах.
Из приведенных выше формул для скорости звука следует:
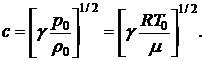
Эта формула известна как формула Лапласа, так как именно Лаплас показал необходимость введения множителя γ для адиабатического распространения звука.
7. Какова скорость звука внутри цилиндра двигателя внутреннего сгорания сразу же после вспышки, когда давление р равно 200 атм и температура 1000 °С, если для газовой смеси γ = сp /сv = 1,35, а плотность смеси при 0 °С и атмосферном давлении p0 = 105 Па равна ρ0 = 0,0014 г/см3 ?
Решение. Считая процесс адиабатическим, находим плотность газовой смеси после вспышки ρ = ρ0 (p/p0)1/g.
Откуда скорость звука с = (gp/ρ)1/2 ≈ 620 м/с.
Задачи для самостоятельного решения
9.1. Смещение частиц в плоской бегущей в воздухе звуковой волне имеет вид:
ξ(x,t)=5•10-8sin(1980t-6x) [м].
Найти: частоту колебаний; скорость распространения волны; длину волны; амплитуду скорости колебания каждой частицы; ускорение; амплитуду звукового давления. Для воздуха ρ0c = 420 кг/(м2с).
Ответ : f = 315 Гц, с = 330 м/с, λ = 1 м, ν0 = 9,9•10-5 м/c, a0 = 0,2 м/с2,
р0’ = 0,04 Па.
9.2. Плоская волна с амплитудой акустического давления 2*10-5 Па при 1000 Гц (порог слышимости) распространяется в воздухе. Найти значения амплитуды скорости и смещения частиц.
Ответ: ν0 = 4,8•10-8 м/с, ξ0 = 7,6•10-12 м.
9.3. Сравнить колебательные скорости частиц в бегущей звуковой волне в воде и воздухе при одинаковом акустическом давлении. (Принять ρ0c для воды равным 1,5• 106 кг/(м2•с), для воздуха 420 кг/(м2•с).
Ответ: νвозд / νвода ≈ 3600.
9.4. Амплитуда звукового давления в плоской гармонической волне равна р'0 = 2•10-4 Па . Вычислить амплитуды колебательной скорости и смещения, средние интенсивность и плотность энергии волны в воздухе на частоте f = 1 кГц .
Ответ: ν0 = 4,7•10-7 м/с, ξ0 = 7•10-11 м, J = 4,8•10-11 Вт/м2 ,
E = 1,4•10-13 Дж/м3 .
9.5. Интенсивность звука J равна 0,1 Вт/м2. Вычислить объемную плотность энергии E , давление р'0 , смещение ξ0 , скорость ν0 частиц в плоской волне на частоте f = 10 кГц в воде и в воздухе. Скорость звука в воде 1500 м/с, в воздухе 340 м/с.
Ответ: в воде: 6,7•10-5 Дж/м3, 5,5•102 Па, 5,8•10-9 м, 3,7•10-4 м/с;
в воздухе: 3•10-4 Дж/м3, 9,2 Па, 3,5•10-7 м, 2,2•10-2 м/с.
9.6. Интенсивность звука равна 2•10-4 Вт/м2. Найти уровень интенсивности относительно стандартного нулевого уровня Jст =10-12 Вт/м2.
Ответ: В = 83 дБ.
9.7. Рассчитать адиабатический модуль объемной упругости (внутреннее давление) для воздуха (с = 330 м/с, ρ0 = 1,3 кг/м3, g = 1,4) и воды (с = 1500 м/с, ρ0 = 1000 кг/м3).
Ответ. Для воздуха Ka= ρ0c2 = 1,4•105 Па.
В случае идеального газа (см.задачу 9.12) внутреннее давление Ka связано с равновесным давлением p0 формулой p0 = Ka /g , откуда p0 = 1 атм.
В случае воды получаем гораздо большую величину Ka = 2,25•109Па = 23•103 атм. Поэтому для волн, распространяющихся в воде, линейное приближение справедливо в гораздо более широком диапазоне приращения давления, чем для волн, распространяющихся в воздухе.
9.8. Получить приближенную формулу для скорости звука в воздухе, учитывая, что g = 1,4 и μ = 28,8 г/моль.
Ответ. Скорость звука (м/с) рассчитывается по формуле
c ≈ 20T01/2,
где T0 - температура в Кельвинах.
9.9. При какой температуре скорость звука в воздухе удвоится по сравнению со скоростью при 0°С и при какой станет в два раза меньше? Скорость звука при t =0°С равна c0 = 330 м/с.
Ответ. с = 2 c0 при t = 819°С,
с = c0 /2 при t = - 205°С (если бы воздух оставался идеальным газом).
9.10. В два свистка одинаковой длины вдуваются: воздух, охлажденный до температуры жидкого воздуха (t1 = -180oС), и теплый воздух. Один свисток издает звук на октаву выше, чем другой. Какова должна быть температура воздуха t2, вдуваемого во второй свисток?
Ответ. Отношение резонансных частот свистков пропорционально отношению скоростей звука в них, отсюда получаем t2 = 99°С.
9.11. Рассчитать "звуковой барьер" самолета (когда скорость его равна скорости звука) на высоте 9 км, где температура -70°С, и сравнить его со звуковым барьером при 0oС на уровне моря. Зависит ли барьер от атмосферного давления?
Ответ. Около 1000 и 1200 км/ч независимо от давления.
9.12. При интерференции двух плоских звуковых волн, излучаемых двумя одинаковыми закрытыми трубами длиной l=60 см, вследствие различия температуры воздуха в них создается 1 биение в секунду. Температура воздуха в трубе, дающей более низкий тон, равна 16 °С.
Какова температура воздуха в другой трубе? Считать, что генерируется первая мода колебаний закрытой трубы, т.е. длина волны звука λ=l/2.
Ответ: t2 = 16,5 °С .
Контрольные вопросы
1. Основные уравнения гидродинамики сжимаемой жидкости в линейном приближении.
2. Звуковые волны.
3. Энергия и импульс звуковых волн.
Список литературы
1. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т.VI. Гидродинамика. М.:Наука, 1986. 736 с.
2. Бреховских Л.М., Гончаров В.В. Введение в механику сплошных сред (в приложении к теории волн). М.:Наука, 1982. 335 с.
3. Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. Т. 1, 2. М.:Наука, 1963.
4. Лойцянский Л.Г. Механика жидкости и газа / М.:Наука, 1973. 847 с.
5. Акустика в задачах. / Под ред. Гурбатова С.Н., Руденко О.В. М.:Наука, Физматлит, 1996. 336 с.
6. Механика сплошных сред в задачах. Т. 1, 2: / Под ред. Эглит М. Э. М.: “Московский Лицей”, 1996.
Оглавление
Предисловие. 2
1. Лагранжев и Эйлеров способы описания движения жидкости. Основные уравнения гидродинамики идеальной жидкости. 3
2. Гидростатика. 14
3. Уравнение Бернулли и закон сохранения импульса. 21
4. Потенциальное течение идеальной несжимаемой жидкости. 33
5. Плоское потенциальное течение идеальной несжимаемой жидкости. Функция тока. Комплексный потенциал. 44
6. Вихревое движение жидкости. 53
7. Поверхностные гравитационные волны.. 61
8. Течение вязкой несжимаемой жидкости. 68
9. Линейная акустика идеальной среды.. 82
Список литературы.. 94
Оглавление. 95
