Метод эквивалентного источника
(АКТИВНОГО ДВУХПОЛЮСНИКА)
Двухполюсником называется цепь, которая соединяется с внешней относи-
тельно неё частью цепи через два вывода – полюса. Различают активные и пас-
сивные двухполюсники. Активный двухполюсник содержит источники элект-
рической энергии, а пассивный двухполюсник их не содержит. Условные обоз-
начения активного А и пассивного П двухполюсников приведены на рис. 17.1.
Для расчёта цепей с двухполюсниками последние представляют схемами заме-
щения [3, 6, 20].
Схема замещения линейного двухполюсника определяется его линейной вольт-амперной или внешней характеристикой 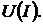
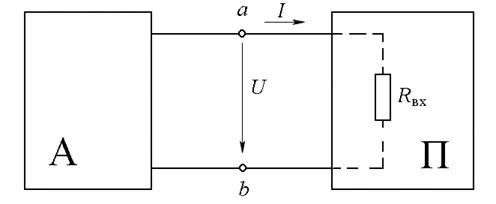
Рис. 17.1
Вольт-амперная характеристика пассивного двухполюсника – прямая. Его схема замещения представляется резистивным элементом с сопротивлением
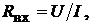
где 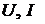 и
и 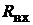 – напряжение между выводами, ток и входное сопротивление
– напряжение между выводами, ток и входное сопротивление
пассивного двухполюсника.
Вольт-амперную характеристику активного двухполюсника (рис.17.2, а)
можно построить по двум точкам, соответствующим режимам холостого хода,
т. е. при 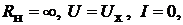 и короткого замыкания, т.е. при
и короткого замыкания, т.е. при 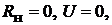
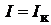 . Эта характеристика (рис. 17.2, б ) и её уравнение
. Эта характеристика (рис. 17.2, б ) и её уравнение
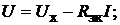 (17.1)
(17.1)
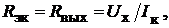 (17.2)
(17.2)
где 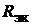 – эквивалентное или выходное сопротивление двухполюсника, совпада-
– эквивалентное или выходное сопротивление двухполюсника, совпада-
ют c одноимёнными характеристиками и уравнением (3.1) источника электри-
ческой энергии, представляемого схемами замещения на рис. 3.3, а. Итак, ак-
тивный двухполюсник представляется эквивалентным источником с ЭДС 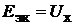 и внутренним сопротивлением
и внутренним сопротивлением 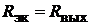 (рис.17.2, а).
(рис.17.2, а).
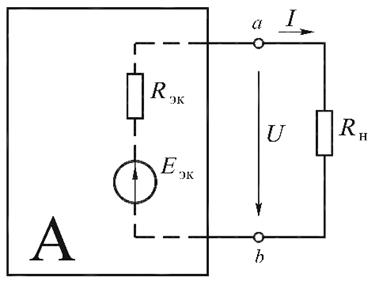
а)
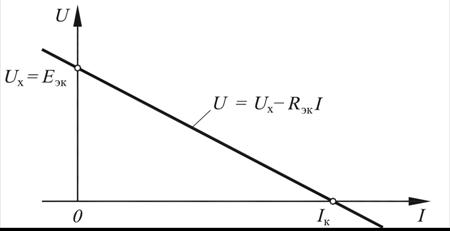
б)
Рис. 17.2
Если приёмник с сопротивлением нагрузки 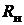 подключён к активному двухполюснику, то его ток определяется по методу эквивалентного источника:
подключён к активному двухполюснику, то его ток определяется по методу эквивалентного источника:
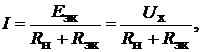 (17.3)
(17.3)
что следует из закона Кирхгофа. Эквивалентную схему с источником ЭДС на-
зывают схемой Гельмгольца – Тевенена.
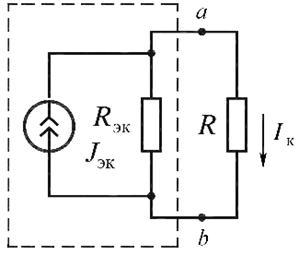
Метод эквивалентного источника тока. Для расчёта тока в ветви  , соп-
, соп-
ротивление которой 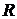 , надо заменить часть схемы относительно зажимов a и
, надо заменить часть схемы относительно зажимов a и 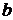 (при разомкнутой ветви a и
(при разомкнутой ветви a и 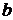 ) эквивалентным источником тока, ток кото-
) эквивалентным источником тока, ток кото-
рого 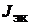 , а проводимость
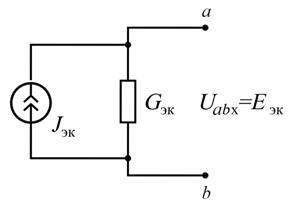
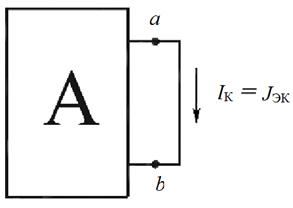
, а проводимость 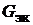 (рис. 17.3, а).
(рис. 17.3, а).
а б
в г
Рис. 17.3
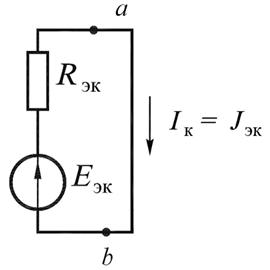
Для нахождения тока 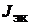 надо зажимы a и
надо зажимы a и 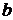 закоротить и любым способом
закоротить и любым способом
рассчитать ток короткого замыкания  , протекающий по закороченому участ-
, протекающий по закороченому участ-
ку (см. рис. 17.3, б). При этом 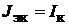 . Сопротивление
. Сопротивление 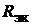 можно найти по
можно найти по
методу эквивалентного источника ЭДС по формуле (17.2). Это же сопротивле-
ние может быть рассчитано, как это видно из схемы замещения заданной схе-
мы в режиме короткого замыкания (рис.17.3, в), по формуле:
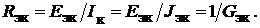 (17.4)
(17.4)
Ток в ветви 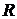 (см. рис. 17.3, г)
(см. рис. 17.3, г)
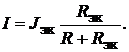 (17.5)
(17.5)
Эквивалентная схема с источником тока (см. рис. 17.3, г) – схема Нортона.
Пример 38.Определить ток на нагрузке 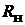 в схеме рис. 17.4.
в схеме рис. 17.4.
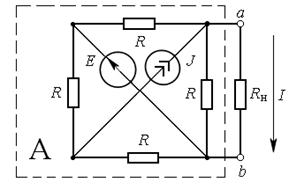
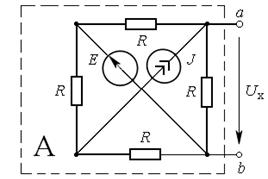
а) б)
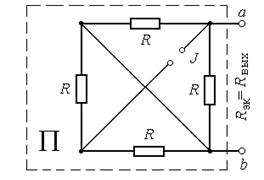
в)
Рис.17.4
Решение. Поскольку приёмник с сопротивлением нагрузки 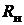 подключен к активному двухполюснику (см. рис. 17.4, а), то его ток определяется по методу
подключен к активному двухполюснику (см. рис. 17.4, а), то его ток определяется по методу
эквивалентного источника:
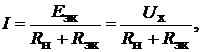
что следует из второго закона Кирхгофа.
Для расчёта напряжения холостого хода 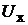 между выводами a и b активно-
между выводами a и b активно-
го двухполюсника разомкнём ветвь с резистивным элементом 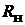 (см. рис.17.4, б). Применяя метод наложения и учитывая симметрию схемы, находим:
(см. рис.17.4, б). Применяя метод наложения и учитывая симметрию схемы, находим:

Заменив источники ЭДС и тока активного двухполюсника резистивными
элементами с сопротивлениями, равными внутренним сопротивлениям соот-
ветствующих источников (нулевым − для источника ЭДС и бесконечно боль-
шим − для источника тока), получим выходное сопротивление (сопротивление, измеренное на выводах a и b) (см. рис. 17.4, в)
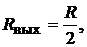
а также искомый ток
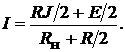
Пример 39.Для схемы цепи рис. 17.5, а методом эквивалентного источни-
ка ЭДС найти ток в ветви резистора, сопротивление которого 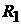 , если
, если
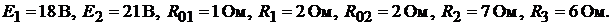
Решение. Обозначим положительное направление искомого тока на исход-
ной схеме (см. рис. 17.5, а). Рассмотрим часть схемы, подключенную к исследу-
емой первой ветви (обведённую пунктирной линией), в качестве эквивалентно-
го источника ЭДС 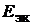 с сопротивлением
с сопротивлением 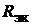 . Нарисуем эквивалентную элект-
. Нарисуем эквивалентную элект-
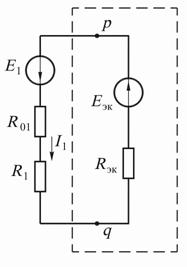
рическую схему с эквивалентным источником напряжения (см. рис. 17.5, б).
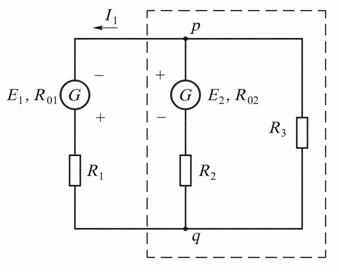
а б
в г д
Рис. 17.5
На схеме произвольно выбрано положительное направление ЭДС эквива-
лентного источника 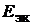 в точке p. Это позволяет записать для режима холос-
в точке p. Это позволяет записать для режима холос-
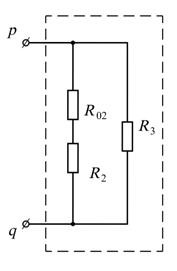
того хода эквивалентного источника с отключенной первой ветвью (см. рис. 17.5, в)

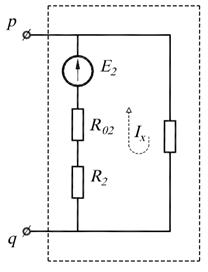
Развёрнутая схема эквивалентного источника в режиме холостого хода по-
казана на рис. 17.5, г. Во внутренних ветвях источника ток
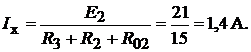
Напряжение холостого хода определяет ЭДС источника:

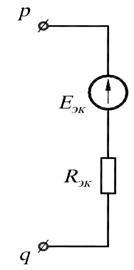
Найдём сопротивление 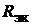 эквивалентного источника. Для подсчёта сопро-
эквивалентного источника. Для подсчёта сопро-
тивления источника преобразуем его схему (см. рис. 17.5, г), заменив источник напряжения 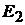 короткозамкнутым участком (рис. 17.5, д). Входное сопротив-
короткозамкнутым участком (рис. 17.5, д). Входное сопротив-
ление последней схемы является сопротивлением эквивалентного источника
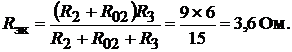
Возвращаясь к схеме рис. 17.5, б, найдём искомый ток по закону Ома
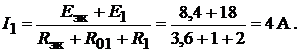
Пример 40.Методами эквивалентного источника ЭДС и эквивалентного ис-
точника тока найти ток в ветви 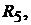 если
если 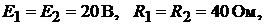
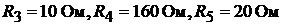 (рис.17.6, а).
(рис.17.6, а).
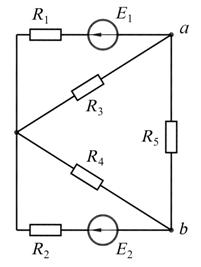
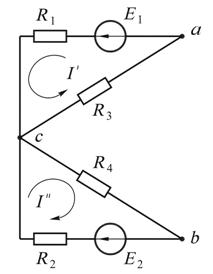
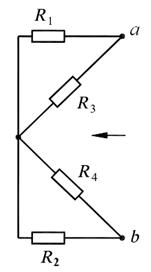
а б в
Рис. 17.6
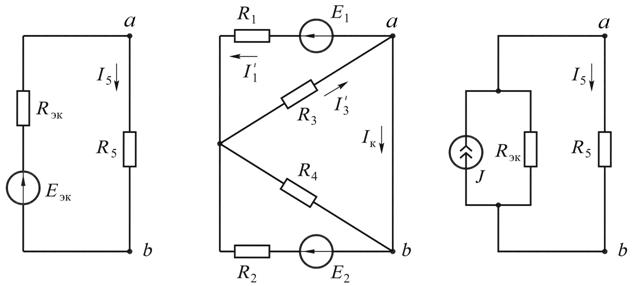
г д е
Рис. 17.6
Решение. 1. Расчёт методом эквивалентного источника ЭДС. Отключим ветвь с 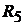 (см. рис. 17.6, б) и найдём её параметры оставшейся схемы − ЭДС
(см. рис. 17.6, б) и найдём её параметры оставшейся схемы − ЭДС 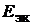 (т.е. напряжение
(т.е. напряжение 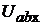 холостого хода между точками a и b) и
холостого хода между точками a и b) и 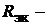 сопротивление схемы рис. 17.6, в между точками a и b в режиме холостого хода при закороченных ЭДС
сопротивление схемы рис. 17.6, в между точками a и b в режиме холостого хода при закороченных ЭДС 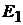 и
и 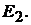 Схема эквивалентного источника ЭДС приведена на рис. 17.6, г. ЭДС эквивалентного источника и его сопротивление равны:
Схема эквивалентного источника ЭДС приведена на рис. 17.6, г. ЭДС эквивалентного источника и его сопротивление равны:
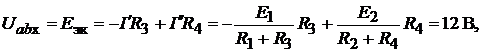
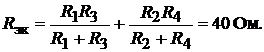
Искомый ток согласно формуле (17.3)
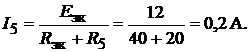
2.При расчёте методом эквивалентного источника тока ветвь 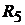 закорачи-
закорачи-
ваем (см. рис. 17.6, д). Ток  , проходящий по закороченной ветви ab,является током эквивалентного источника тока
, проходящий по закороченной ветви ab,является током эквивалентного источника тока 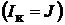 . Найдём его. Это можно сделать,
. Найдём его. Это можно сделать,
расcчитав двухузловую схему рис. 17.6, 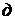 методом узловых потенциалов. При-
методом узловых потенциалов. При-
няв потенциал точек a и 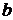 равным нулю
равным нулю 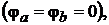 найдём:
найдём:
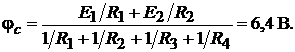
Для определения тока 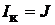 вычисляем
вычисляем 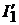 и
и 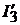 и по первому закону Кирх-
и по первому закону Кирх-
гофа определяем:
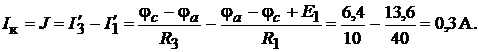
Сопротивление эквивалентного источника тока 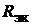 равно сопротивлению эквивалентного источника напряжения; однако его можно найти по выражению (17.4):
равно сопротивлению эквивалентного источника напряжения; однако его можно найти по выражению (17.4):
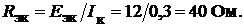
Из схемы эквивалентного источника тока (см. рис. 17.6, е) по формуле (17.5) находим искомый ток
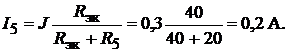
Пример 41.В цепи (рис. 17.7) ток 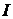 равен
равен 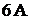 при разомкнутом ключе
при разомкнутом ключе 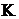 и
и 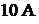 при замкнутом. Определить параметры активного двухполюсника относи-
при замкнутом. Определить параметры активного двухполюсника относи-
тельно полюсов 1 и 2 при значении параметров 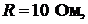
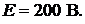
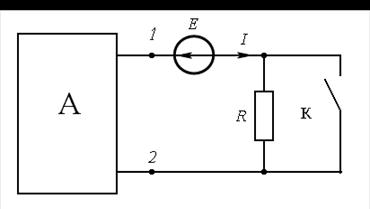
Рис. 17.7
Решение. Решение основано на применении метода эквивалентного генера-
тора:
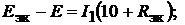
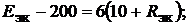
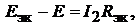

Ответ: 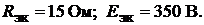
Пример 42.В цепи (рис.17.8) известны показания амперметров  и
и 
при различных положениях ключей 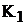 и
и 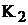 . При разомкнутых ключах
. При разомкнутых ключах 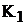 и
и 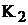 показания амперметров равны
показания амперметров равны 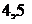 и
и 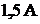 соответственно. При замкнутых ключах
соответственно. При замкнутых ключах 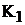 и
и 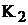 показания амперметров равны
показания амперметров равны 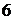 и
и 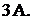 Величины сопротивле-
Величины сопротивле-
ний 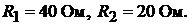
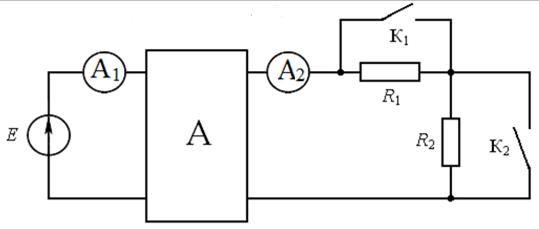
Рис. 17.8
Определить показания амперметров  и
и  при замкнутом ключе
при замкнутом ключе 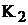 и разомкнутом ключе
и разомкнутом ключе 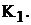
Решение. Решение основано на использовании теорем об активном двухпо-
люснике и теоремы о линейных соотношениях.
В соответствии с теоремой об эквивалентном генераторе для токов, протека-
ющих через амперметр 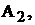 при различных положениях ключей
при различных положениях ключей 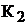 и
и 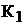 мож-но записать:
мож-но записать:
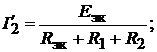 (17.1)
(17.1) 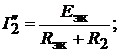 (17.2)
(17.2) 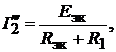 (17.3)
(17.3)
эдесь 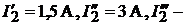 искомый ток.
искомый ток.
Определяя из уравнений (17.1) и (17.2) значения параметров эквивалентного генетора 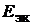 и
и 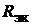 , из уравнения (17.3) найдём значение тока
, из уравнения (17.3) найдём значение тока 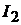 при разомк-
при разомк-
нутом ключе 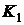 и замкнутом
и замкнутом 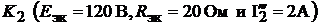 . Для вы-
. Для вы-
числения 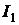 воспользуемся принципом линейности, согласно которому измене-
воспользуемся принципом линейности, согласно которому измене-
нения всех токов связаны между собой простыми линейными уравнениями, ес-
ли это изменение токов вызвано изменением параметров (сопротивления или ЭДС) только одной ветви (или изменением тока в одном источнике тока). Та-
ким образом, для токов 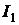 и
и 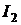 можно записать
можно записать 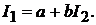 Расписывая для различных положениях ключей
Расписывая для различных положениях ключей 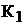 и
и 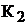 данное уравнение и определяя коэф-
данное уравнение и определяя коэф-
фициенты a и 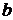 , найдём искомое значение тока
, найдём искомое значение тока
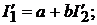 (17.4)
(17.4) 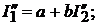 (17.5)
(17.5) 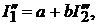 (17.6)
(17.6)
или
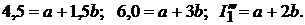
Из формул (17.4), (17.5) определяем 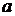 и
и 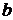
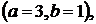 из формулы (17.6) оп-
из формулы (17.6) оп-
ределяем 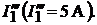
Ответ: 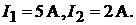
ЧЕТЫРЁХПОЛЮСНИКИ
Четырёхполюсники ─ это обобщённое наименование электрической цепи, рассматриваемой по отношению к четырём её зажимам [1, 20]. Трансформатор, линию передачи энергии, мостовую схему и т. п. можно рассматривать как четырёхполюсники.
Принято изображать четырёхполюсник в виде прямоугольника с выходящи-
ми из него концами (полюсами) mn и 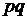 (рис. 18.1). Если четырёхполюсник со-
(рис. 18.1). Если четырёхполюсник со-
держит источники энергии, то в прямоугольнике ставят букву А (активный), если буква А отсутствует, то это значит, что четырёхполюсник пассивный.
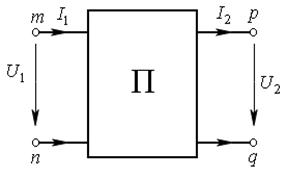
Рис. 18.1
На практике четырёхполюсник обычно работает в режиме, когда одна пара зажимов, например 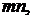 является входной, а другая пара, например
является входной, а другая пара, например 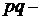 вы- ходной. Входной ток обозначают
вы- ходной. Входной ток обозначают 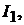 входное напряжение
входное напряжение 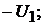 ток и напря-
ток и напря-
жение на выходе 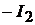 и
и 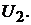
Четырёхполюсник является передаточным звеном между источником пита-
ния и нагрузкой. К входным зажимам 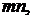 как правило, присоединяют источ-
как правило, присоединяют источ-
ник питания, к выходным зажимам ─ нагрузку.
Приведём две из шести форм записи уравнений пассивного четырёхполюс-
ника.
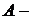 форма:
форма: 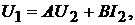 (18.1)
(18.1)
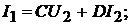 (18.2)
(18.2)
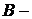 форма:
форма: 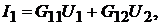 (18.3)
(18.3)
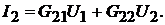 (18.4)
(18.4)
Для четырёхполюсников коэффициенты связаны соотношением
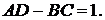 (18.5)
(18.5)
Пример 43. Реальный источник электрической энергии (рис. 18.2) имеет напряжение холостого хода 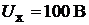 и внутренние потери при холостом
и внутренние потери при холостом
ходе и коротком замыкании 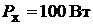 и
и 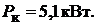
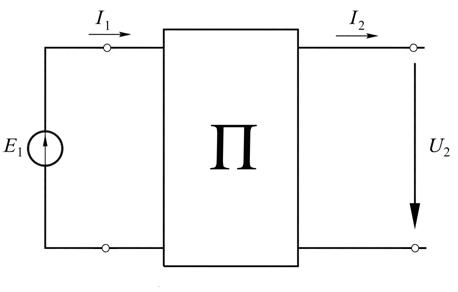
Рис. 18.2
Определить ток короткого замыкания этого источника.
Решение. В решении используется теория четырёхполюсников. Представля-
ем несовершенный источник в виде идеального источника, нагруженного на произвольный пассивный четырёхполюсник, входные полюса которого являют-
ся выходными полюсами источника.
Для четырёхполюсника можно записать следующие соотношения
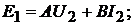
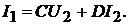
По отношению к режиму холостого хода и короткого замыкания эти уравне-
нения отражают следующие соотношения
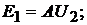
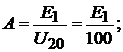
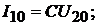
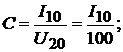
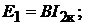
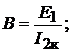

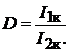
Дополнительно к полученным соотношениям запишем условие взаимности
(обратимости) пассивного четырёхполюсника в виде 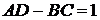 :
:
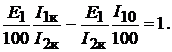
Учитывая, что 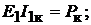
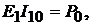 имеем
имеем 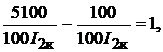 откуда
откуда 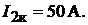
Пример 44.В электрической цепи (рис. 18.3) известны значения парамет-
ров: 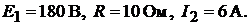 Четырёхполюсник симметричный и пас-
Четырёхполюсник симметричный и пас-
сивный. Определить ток 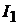 после замыкания ключа
после замыкания ключа 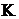 , если при этом
, если при этом  .
.
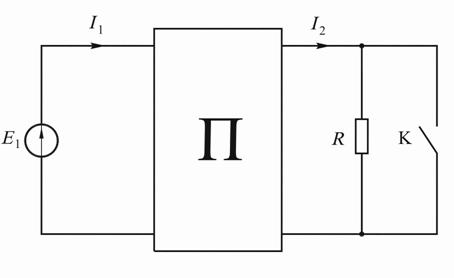
Рис. 18.3
Решение. Задача решается с использованием принципа взаимности и ком-
пенсации:
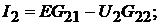
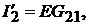
где 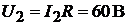 , откуда
, откуда
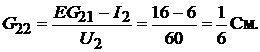
Так как четырёхполюсник симметричный и взаимный, то
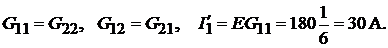
Пример 45.В цепи (рис. 18.4) известно: 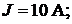 при положении ключа 1 и
при положении ключа 1 и
2 показания амперметра соответственно равны 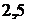 и
и 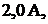 а мощность, отдава-емая источником тока, 175 и 180 Вт. Определить сопротивление резистора
а мощность, отдава-емая источником тока, 175 и 180 Вт. Определить сопротивление резистора 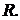
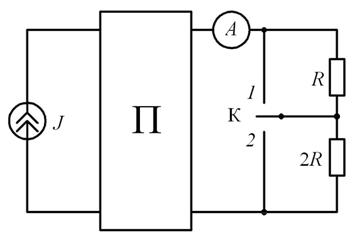
Рис. 18.4
Решение. В положении ключа 1 напряжение на входе четырёхполюсника равно
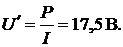
В положении 2 : 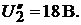 Соответственно, на выходе для положений 1 и 2:
Соответственно, на выходе для положений 1 и 2:
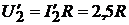 и
и 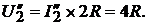
Из уравнений четырёхполюсника следует: 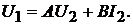
Эти уравнения для первого и второго режима можно записать
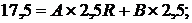
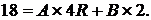
После деления первого уравнения на 2,5, второго на 2 имеем:
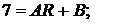
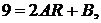
откуда 
Второе уравнение 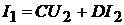 можно записать в следующем виде:
можно записать в следующем виде:
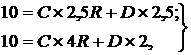
или
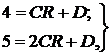
откуда 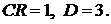
Из уравнения взаимности можно определить сопротивление 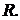
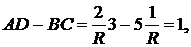 откуда
откуда 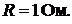
Все искомые величины найдены.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Указать, какие физические законы положены в основу первого и второго законов Кирхгофа.
2. Указать отличительные особенности метода эквивалентного источника (активного двухполюсника) по сравнению с остальными методами расчёта цепей постоянного тока.
3. Указать, в чём заключаются достоинства графо-аналитического метода расчёта цепей постоянного тока:
1) удобство пользования;
2) возможность программирования метода и дальнейшего использования в программных комплексах расчёта электрических цепей.
4. В чём преимущества представления электрической цепи в виде четырёх-
полюсника?
СПИСОК ЛИТЕРАТУРЫ
1. Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бес-
сонов. − М.: Гардарики, 2007. − 701 с.
2. Теоретические основы электротехники. Т. 1. Основы теории линейных цепей: учебник / Под ред. П.А. Ионкина. − М.: Высшая школа, 1976. − 544 с.
3. Касаткин, А. С., Немцов, М. В. Курс электротехники: учебник / А.С. Касаткин, М.В. Немцов.− М.: Высшая школа, 2005. − 542 с.
4. Фриск, В.В. Основы теории цепей: учебное пособие / В.В. Фриск. − М.: РадиоСофт, 2002. − 288 с.
5. Евдокимов, Ф.Е. Теоретические основы электротехники: учебник / Ф.Е. Евдокимов М.: Издат. Центр «Академия», 2004. − 560 с.
6. Шебес М.Р. Задачник по теории линейных электрических цепей / М.Р. Шебес. − М.: Высшая школа, 1982. − 488 с.
7. Сборник задач и упражнений по теоретическим основам электротехники:
учебное пособие / под ред. П.А. Ионкина. − М.: Энергоатомиздат, 1982. − 768 с.
8. Иванов, И.Н. Электротехника. Основные положения, примеры и задачи / И.Н. Иванов, А.Ф. Лукин, Г.И. Соловьёв. − СПб.: Лань, 1999. − 192 с.
9. Рекус Г.Г., Белоусов А.И. Сборник задач и упражнений по электротехнике и основам электроники: учебное пособие / Г.Г. Рекус, А.И. Белоусов. − М.: Высшая школа, 2001. − 416 с.
10. Зевеке Г. В., Ионкин П. А., Нетушил А. В., Страхов С.В. Основы теории цепей: учебник / Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. − М.
− Л.: Энергия, 1965. − 444 с.
11. Власов С.П. Сборник задач с решениями по теоретическим основам электротехники: учебное пособие / С.П. Власов. − М.: МИИТ, 1974. − 166 с.
12. Прянишников В.А. Электротехника и ТОЭ в примерах и задачах: практи-
ческое пособие / В.А. Прянишников, Е.А. Петров, СПб.: КОРОНА принт, 2003. − 336 с.
13. Березкина Т.Ф. Задачник по общей электротехнике и основам электрони-
ки: учебное пособие / Т.Ф. Берёзкина, Н.Г. Гусев, В.В. Масленников. М.: Выс-
шая школа, 2001. − 380 с.
14. Чони Л. В. Теоретические основы электротехники: учебное пособие / Л.В. Чони. − Казань: Изд-во Казан. гос. техн. ун-та, 2007. − 77 с.
15. Сборник задач с решениями по общей электротехнике: учебное пособие / под ред. В. К. Пономаренко. − М.: Высшая школа, 1972. − 184 с.
16. Лоторейчук Е.А. Теоретические основы электротехники / Е.А. Лоторей-
чук. − М.: Высшая школа, 2000. − 224 с.
17. Сборник задач по общей электротехнике: учебное пособие / Под ред. В.С. Пантюшина. − М.: Высшая школа, 1973. − 280 с.
18. Рабинович Э.А. Сборник задач и упражнений по электротехнике / Э.А. Рабинович. − М.: Энергия, 1972. − 304 с.
19. Сборник задач по электротехнике и основам электроники. Учебное посо-
бие / под ред. В.Г. Герасимова. − М.: Высшая школа, 1987. − 286 с.
20. Николаев С.С., Пищиков В.И. Сборник задач повышенной сложности по теоретической электротехнике / С.С. Николаев, В.И. Пищиов. − М.: Знак, 2000.
64 с.
Оглавление
Введение ……………………………………………………………………..............
1. Базисные понятия и определения теории электрических цепей ………………
2. Пассивные элементы электрической цепи ……………………………………...
3. Активные элементы электрической цепи ………………………………………. Закон Ома для участка цепи. Обобщённый закон Ома……………………...........
5. Законы Кирхгофа для электрической цепи …………………………………… Метод эквивалентного преобразования схем…………………………………….
7. Применение законов Ома и Кирхгофа при расчёте электрических цепей …..
8. Работа и мощность электрического тока. Энергетический баланс……………
9. Метод контурных токов ………………………………………………………....
10. Принцип и метод наложения (суперпозиции) ………………………………..
11. Входные и взаимные проводимости ………………………………………….
12. Теорема взаимности ……………………………………………………………
13. Теорема компенсации .………………………………………………………....
14. Линейные соотношения в электрических цепях ...…………………………..
15. Изменения токов ветвей, вызванные приращением сопротивления одной ветви (теорема вариаций)…..……………………………………………………....
16. Метод узловых потенциалов …………………………………………………..
17. Метод эквивалентного источника (активного двухполюсника) …………….
18. Четырёхполюсники ……………………………………………………………
Контрольные вопросы…………………………………………………………….
Список литературы ………………………………………………………………..
КУРИР Валерий Иосипович
