Входные и взаимные проводимости

Рассмотрим скелетную схему пассивной цепи (рис. 11.1, а). На ней показаны

ветви и узлы. В каждой ветви имеется сопротивление. Выделим в схеме две

ветви: m и k. Поместим в ветвь m ЭДС 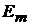(других ЭДС в схеме нет). Выберем

контуры в схеме так, чтобы k- ветвь входила только в k-контур, а m - ветвь −

только в m-контур. ЭДС 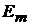вызовет токи в ветвях [1] 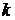и m:

(11.1)

а б в

Рис. 11.1

Коэффициент G имеет размерность проводимости. Коэффициент G с одина-

ковыми индексами называют входной проводимостью ветви (ветви m). Он численно равен току в ветви m, возникшему от действия единичной ЭДС

. Коэффициенты G с разными индексами называют взаимными прово-

димостями. Так, есть взаимная проводимость k- и m-ветвей. Взаимная проводимость численно равна току в k-ветви, возникшему от действия единичной ЭДС в m-ветви.

При расчётном определении проводимостей составляют уравнения по мето-

ду контурных токов, следя за тем, чтобы ветви, взаимные и входные проводи-мости которых представляют интерес, входили каждая только в свой контур.

Далее находят определитель системы 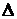и по нему необходимые дополне-

ния:

(11.2)

(11.3)

По формуле (11.3) может получиться либо положительной, либо отри-

цательной величиной. Отрицательный знак означает, что ЭДС 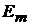, направлен-

ная согласно с контурным током в m-ветви, вызывает ток в k-ветви, не совпа-

дающий по направлению с произвольно выбранным направлением контурного тока 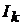по k-ветви.

ТЕОРЕМА ВЗАИМНОСТИ

Теорема взаимности формулируется следующим образом [1]: для любой ли -

нейнойцепи ток в k-ветви, вызванный источником ЭДС 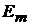, находящимся в

m-ветви, 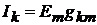равен току 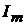в m-ветви, вызванному источником ЭДС 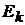(численно равной ЭДС 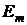), находящимся в k-ветви,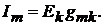

Для доказательства теоремы взаимности обратимся к рис. 11.1, а. Как и при выводах в главее 11, выделим две ветви схемы: ветвь k и ветвь m. Включим в

ветвь m источник ЭДС 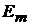, в ветвь 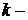амперметр A для измерения тока .

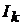Допустим, что каждая из ветвей k и m входит соответственно только в k- и m-

контуры, поэтому по методу контурных токов 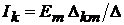. Поменяем мес-

тами источник ЭДС и амперметр, т.е. источник ЭДС переместим из ветви m в ветвь 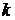и назовём теперь 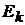, а амперметр – из ветви k в ветвь m. В этом случае ток .

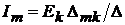Так как 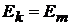, а 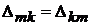в силу симметрии определителя системы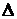

относительно главной диагонали (см. главу 9), то ток 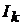в схеме на рис. 11.1, б равняется току 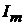в схеме на рис. 11.1, в.

При практическом использовании теоремы взаимности важно иметь в виду взаимное соответствие направлений токов и ЭДС в схемах на рис. 11.1, б, в.

Так, если ЭДС 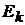источника ЭДС, находящегося в k-ветви схемы рис. 11.1, в,

направлена согласно с контурным током 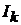в схеме рис. 11.1, б, то положи-

тельное направление отсчёта для тока 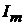в схеме рис. 11.1, в будет совпадать с положительным направлением контурного по ветви тока m (ЭДС 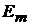в схеме

на рис. 11.1, б направлена по ).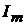

Пример 23.В схеме на рис. 12.1переключател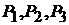и и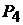могутнахо-

диться в первом или втором положении. Если они находятся в положении 1, то включен только один источник ЭДС 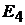.Под действием ЭДС 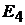протекают токи 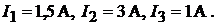Найти ток 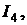если все переключатели нахо-

дятся в положении 2, полагая, что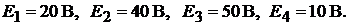

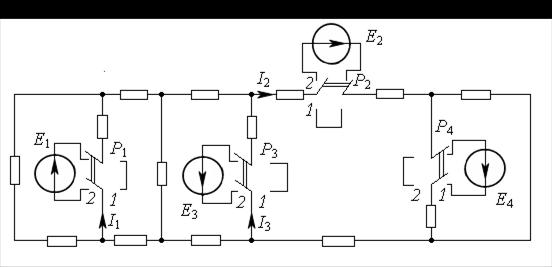
Рис. 12.1

Решение. Для определения тока 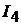воспользуемся принципами наложения и взаимности. Пусть в схеме был включен один источник ЭДС 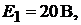а остальные 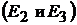отсутствовали, то в ветви 4 (номер ветви соответствует индексу ЭДС) по принципу взаимности протекал бы сверху вниз ток в 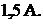Аналогичным образом найдем токи в ветви 4 при включении источников ЭДС и и произведём алгебраическое сложение частичных токов (с учётом их направления):

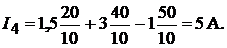
Все искомые величины найдены.

ТЕОРЕМА КОМПЕНСАЦИИ

Рассмотрим два варианта этой теоремы. В любой электрической цепи без из-

менения токораспределения сопротивление можно заменить [1]:

1) источником ЭДС 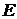, ЭДС которого численно равна падению напряжения на заменяемом сопротивлении и направлена встречно току в этом сопротивле-

нии;

2) источником тока 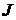, ток которого численно равен току в этом сопротивле-

нии и имеет то же значение, что и ток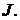

Для доказательства теоремы компенсации выделим из схемы одну ветвь с

сопротивлением по которой течёт ток а всю остальную часть схемы условно обозначим прямоугольником (рис.13.1, а).

а б в г

Рис. 13.1

Если в выделенную ветвь включить два одинаковых и противоположно нап-

равленных источника ЭДС ЭДС которых равна падению напряжения на сопротивлении 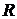под действием тока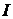 рис. 13.1, , то ток 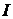в цепи от этого не изменится. Убедимся, что разность потенциалов между точками a и c в схеме на рис. 13.1, б при этом равна нулю. Действительно,

Если то точки a и c можно объединить в одну, т.е. закоротить участок ac и получить схему, где вместо сопротивления 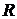включен источник ЭДС 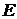(см. рис. 13.1, в). В ней вместо сопротивления R включен источник ЭДС E.

Схема, соответствующая второму варианту теоремы, изображена на рис.

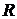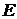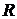13.1, г. Чтобы прийти к ней, заменим последовательно соединённые и на участке ac (см. рис. 13.1, б) параллельным соединением источника тока и сопротивления . Так как то ток через 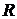будет отсут-

ствовать, поэтому 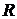можно удалить из схемы. Если ЭДС 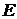на участке включить в состав источника тока, то получим схему рис. 13.1, г, где напряже-

ние .

Пример 24. На схеме (рис. 13. 2, а) даны значения 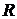(Ом), ЭДС , и токов . Заменить 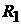источником ЭДС и источником тока.

а б в

Рис. 13.2

Решение. На рис. 13.2, б изображена схема с источником ЭДС а на рис. 13.2, в ─ с источником тока