Для расчётов электричесих цепей

В общем случае схема замещения цепи имеет 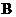ветвей, из которых 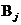вет-

вей содержат источники тока, и 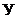узлов. Эквивалентными обозначениями яв-

ляются, соответственно, 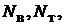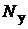(цепь состоит из 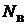ветвей, имеет 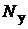уз-

лов и 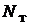источников тока) [3, 6, 9, 13, 15–18 ].

Рассмотрим сначала расчёт цепи без источников тока, т. е. при 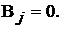Её расчёт сводится к нахождению токов в B ветвях. Для этого необходимо соста-

вить 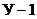независимых уравнений по первому закону Кирхгофа и 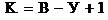независимых уравнений по второму закону Кирхгофа. Соответствующие этим

уравнениям узлы и контуры называются независимыми.

Число независимых уравнений по первому закону Кирхгофа на единицу

меньше числа узлов потому, что ток каждой ветви входит с разными знаками в

уравнения для соединяемых ею узлов. Сумма слагаемых уравнений всех узлов

тождественно равна нулю.

Проведём расчёт цепи (схема её замещения показана на рис. 7.1), которая содержит 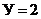узла и 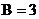ветви, т.е. 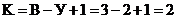независимых контура (1 и 2 или 1 и 3, или 2 и 3).

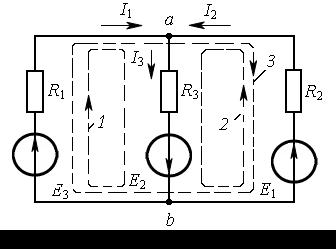
Рис. 7.1

Произвольно выбираем положительные направления токов ветвей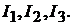

По первому закону Кирхгофа можно составить одно (У – 1 = 2 – 1= 1) неза-

висимое уравнение, например для узла а:

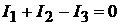, (7.1а)

и по второму закону Кирхгофа – два 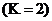независимых уравнения, например для контуров 1 и 2:

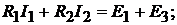(7.1б)

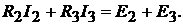(7.1в)

Решая систему трёх уравнений (7.1) с тремя неизвестными токами, напри-

мер методом подстановок, определяем токи ветвей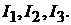

Система уравнений (7.1) в матричной форме имеет вид:

,

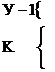
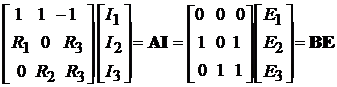или

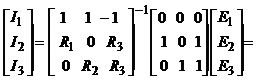
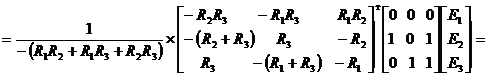
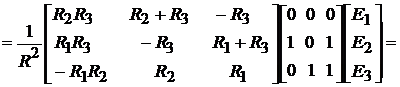
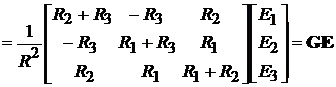, (7.2)

определяет токи ветвей:

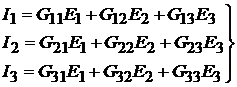, (7.3)

где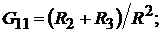

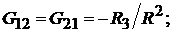
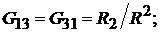
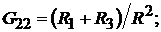
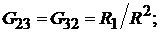
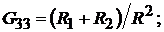
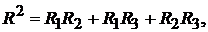
здесь матрица 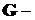матрица так называемых собственных 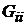и взаимных 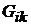проводимостей.

Математическое обеспечение современных ЭВМ имеет стандартные под-

программы решения системы алгебраических уравнений в матричной форме.

При расчёте схем замещения с источниками тока возможны упрощения.

Действительно, токи 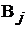ветвей с источниками тока известны, поэтому чис-

ло независимых контуров (без источников тока!), для которых необходимо сос-

тавить уравнения по второму закону Кирхгофа, равно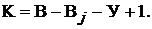

Пример 1.В цепи рис. 7.2, а определить токи 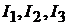при условии, что

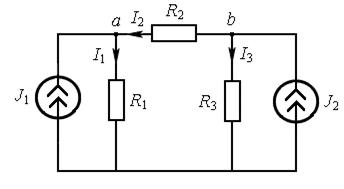
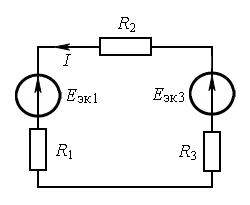
а б
Рис. 7.2

Решение. Идеальный источник тока 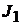с параллельно включённым сопро-

тивлением 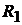заменяем эквивалентным источником ЭДС с последовательно

включённым этим же сопротивлением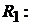

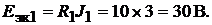
Аналогично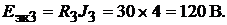

Получили эквивалентную схему (см. рис. 7.2, б), ток в которой определяем по закону Ома

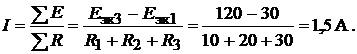
Ток 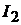в исходной схеме равен току 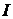в эквивалентной схеме:

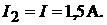
Ток 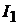определим с помощью уравнения, составленного по первому зако-

ну Кирхгофа для узла 1:

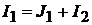
откуда

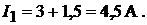
Составив уравнение по первому закону Кирхгофа для узла 2:

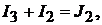
получим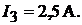

Пример 2.Преобразовать схему цепи, изображённой на рис. 7.3, а, в схему, содержащую только источники ЭДС.

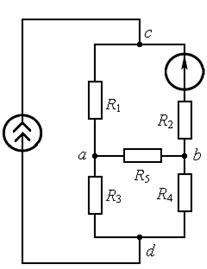
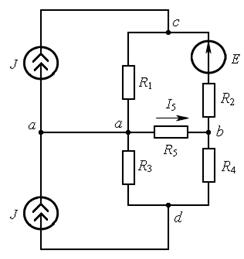
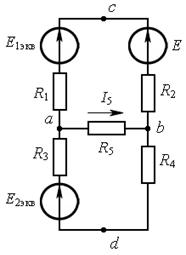а б в

Рис. 7.3

Решение. Проведём эквивалентную замену схемы, изображённой на рис. 7.3, а на соответствующую ей схему, изображённую на рис. 7.3, б. Преобразуем источники тока J последней схемы в источники ЭДС 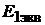и 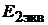(рис. 7.3, в).

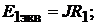
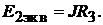
Пример 3.Определить потенциал 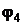точки 4 в цепи, изображённой на рис. 7.4, если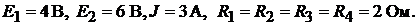

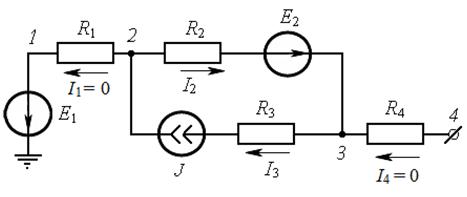
Рис. 7.4

Полагаем, что цепь не замкнута и ток в ветвях 1−2 и 3 −4 отсутствует, т.е.

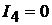
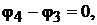
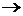
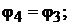
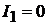
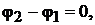
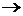
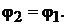
Рассматривая ветвь 2 − 3 как обобщённую (см. рис. 4.2, а), запишем для неё выражение обобщённого закона Ома.

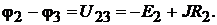
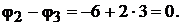
Тогда 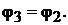Принимаем потенциал земли условно за ноль. Следователь-

но, потенциал точки 4 равен

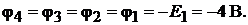
Пример 4.В цепи (рис. 7.5) ЭДС генератора 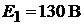, ЭДС батареи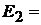

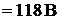, внутреннее сопротивление генератора равно 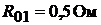, внутреннее

сопротивление батареи соответственно равно 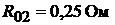. На сборных шинах

устанавливается напряжение 120 В. Определить ток генератора 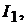аккумуля-

торной батареи 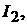потребителя 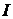и внешнее сопротивление .

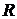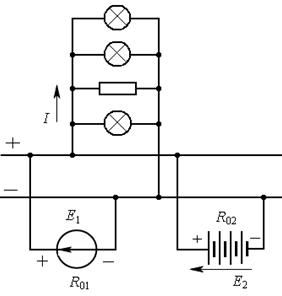
Рис. 7.5

Решение. Напряжение на ветви с источником ЭДС (рис. 7.6) согласно закону Ома:

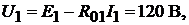
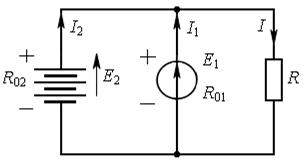
Рис. 7.6

напряжение на ветви с батареей то же:

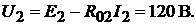
Тогда

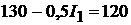
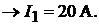
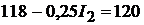
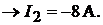
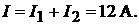
Сопротивление нагрузки 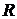равно

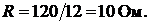
Пример. 5. В схеме (рис.7.7) ЭДС 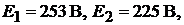их внутренние соп-

ротивления 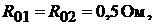сопротивления проводов 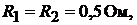соп-

ротивление среднего провода 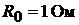, сопротивления остальных проводов: 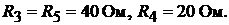Определить токи, применив законы Кирхгофа.

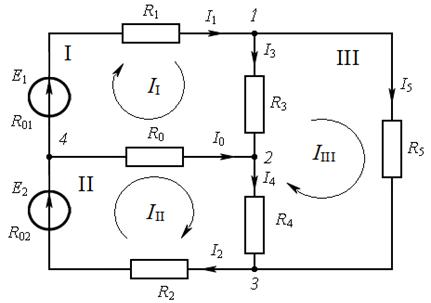
Рис. 7.7

Решение. В схеме имеются шесть ветвей и, следовательно, число неизвест-

ных токов равно шести. Число узлов равно четырём. Намечаем на схеме пред-

полагаемые направления токов в ветвях. После эого составляем, основываясь

на первом законе Кирхгофа, три независимых уравнения. Для узла 1:

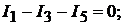для узла 2 : 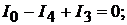для узла 3: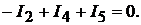

Недостающие уравнения для трёх замкнутых контуров 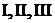составляем

на основании второго закона Кирхгофа. Направление обхода контуров выбира-

ем по часовой стрелке. Для контура 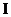: 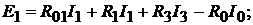для контура 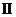: 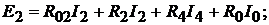для контура :

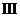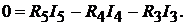
Решение системы уравнений с шестью неизвестными даёт: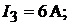

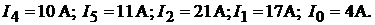
Найденные токи проверим, подставив их в уравнения, составленные на осно-

вании первого закона Кирхгофа:

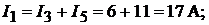
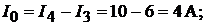
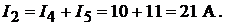
Пример 6.Схема замещения генератора постоянного тока параллельного возбуждения изображена на рис. 7.8. Заданы: номинальное напряжение на вы-

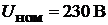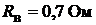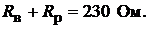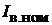водах генератора , номинальный ток якоря , внутреннее сопротивление обмотки якоря . При номинальном режиме общее сопротивление обмотки возбуждения равно: Определить ЭДС ток возбуждения и мощность, выделяемую в нагрузке.

Решение. Уравнение электрического состояния генератора выражается фор-

мулой, составленной по второму закону Кирхгофа:

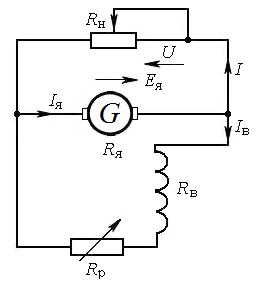
Рис. 7.8

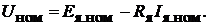
Откуда

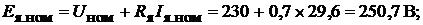
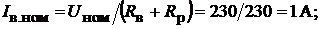
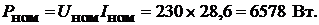
Пример 7.В цепи (рис. 7.9) определить сопротивление 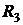и ЭДС гальвани-

ческого элемента 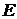, внутренним сопротивлением которого пренебрегаем. Дано: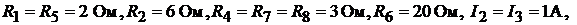

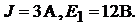
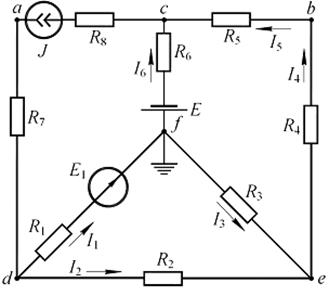
Рис. 7.9

Решение. Составляем для узла 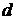уравнение по первому закону Кирхгофа при выбранных положительных направлениях токов: 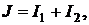откуда нахо-

дим неизвестный ток :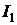

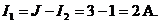
Для контура dfed по второму закону Кирхгофа имеем:

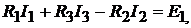
откуда

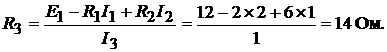
На основании первого закона Кирхгофа для узла e: 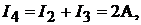а для узла f: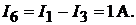

Для определения 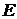составим по второму закону Кирхгофа уравнение для

контура febcf:

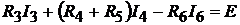
откуда

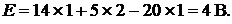
Пример 8.В цепи (рис. 7.10) производится переключение (вместо ампермет-

ра включается вольтметр), известны величины и соотношения между парамет-

рами: 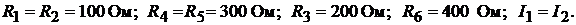Определить показания вольтметра, если показания амперметра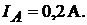

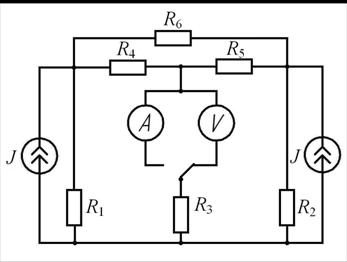
Рис. 7.10

Решение. Решение основано на использовании симметрии цепи. Из условия симметрии ток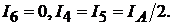

При включённом амперметре напряжение на сопротивлении равно

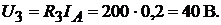
Напряжение на полюсах источника

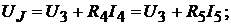
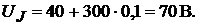
Ток в сопротивлении 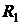равен 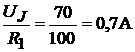. Ток источника тока ра-

вен 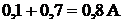. При включённом вольтметре напряжение на полюсах ис-

точника тока равно: 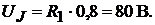Так как токи в сопротивлениях 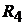и

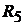равны нулю, следовательно, показание вольтметра равно 80 В.