Показатели безотказности неремонтируемых объектов
Неремонтируемые объекты работают до первого отказа. Различные показатели надежности таких объектов являются характеристиками случайной величины наработки до первого отказа.
Показателями безотказности неремонтируемых объектов являются:
- вероятность безотказной работы 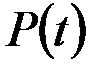 ;
;
- средняя наработка до первого отказа 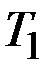 ;
;
- интенсивность отказов 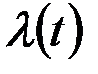 ;
;
- плотность распределения наработки до отказа 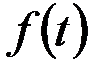 .
.
Вероятность безотказной работы–вероятность того, что в пределах заданного интервала времени или наработки не возникнет отказ объекта. Это убывающая функция, при 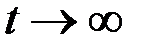
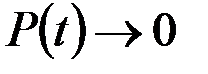 . Значения этой функции находятся в диапазоне от 0 до 1.
. Значения этой функции находятся в диапазоне от 0 до 1.
Таким образом, вероятность безотказной работа определяется в предположении, что в начальный момент времени объект находился в работоспособном состоянии. Обозначим через 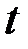 заданное время наработки объекта. Возникновение отказа – случайное событие, а наработка
заданное время наработки объекта. Возникновение отказа – случайное событие, а наработка 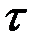 от начального момента до возникновения отказа – случайная величина. Вероятность безотказной работы
от начального момента до возникновения отказа – случайная величина. Вероятность безотказной работы 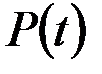 объекта в интервале времени от 0 до
объекта в интервале времени от 0 до 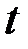 включительно определяется как:
включительно определяется как:
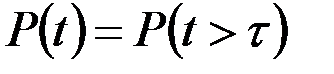 . (3.1)
. (3.1)
Вероятность безотказной работы по статистическим данным об отказах оценивается выражением:
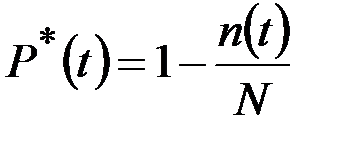 , (3.2)
, (3.2)
где 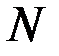 – число объектов, работоспособных в начальный момент времени;
– число объектов, работоспособных в начальный момент времени; 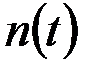 – число объектов, отказавших на отрезке от 0 до
– число объектов, отказавших на отрезке от 0 до 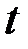 .
.
При этом объем выборки должен быть достаточно велик, и при большом числе изделий статистическая оценка 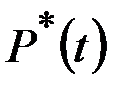 практически совпадает с вероятностью
практически совпадает с вероятностью 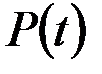 .
.
Наряду с понятием «вероятность безотказной работы» часто используют понятие «вероятность отказа», которое характеризует вероятность того, что объект откажет хотя бы один раз в течение заданной наработки, будучи работоспособным в начальный момент времени. На отрезке времени от 0 до 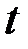 вероятность отказа определяется по формуле:
вероятность отказа определяется по формуле:
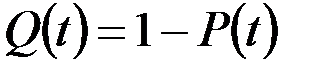 . (3.3)
. (3.3)
Если функция 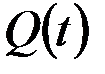 дифференцируемая, то безотказность можно характеризовать плотностью распределения случайной величины наработки до отказа или частотой отказов
дифференцируемая, то безотказность можно характеризовать плотностью распределения случайной величины наработки до отказа или частотой отказов 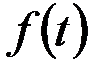 :
:
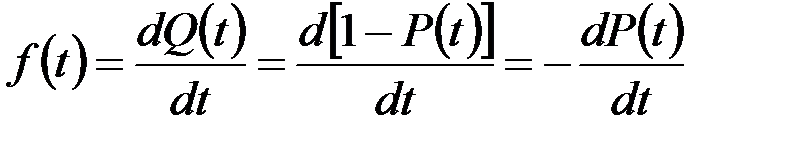 . (3.4)
. (3.4)
Достоинством рассматриваемого показателя является возможность судить по его величине о числе изделий, которые могут отказать за определенный интервал времени.
Из определения вероятности безотказной работы видно, что эта характеристика является убывающей функцией времени и изменяется в диапазоне от 1 в начальный момент времени до 0 при 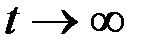 .
.
Такой показатель имеет смысл, если указывается интервал времени, на котором рассматривается безотказность объекта. Если, например, в технических условиях на ремонт электрической машины указывается значение вероятности безотказной работы 0,8 за 9000 ч наработки, то это значит, что из 100 отремонтированных устройств в течение 9000 ч не менее 80 проработают безотказно.
Вероятность безотказной работы входит во многие другие характеристики изделий, учитывает значительное количество факторов, влияющих на надежность, может быть сравнительно просто получена. Однако для восстанавливаемых систем она характеризует только надежность до первого отказа, по ее значению бывает трудно вычислить другие количественные характеристики надежности. Поэтому вероятность безоткатной работы не может полностью характеризовать такое понятие, как надежность, и не может быть с ним отождествлена.
Интенсивность отказов – условная плотность вероятности возникновения отказа объекта, которая определяется как отношение числа отказов изделия в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени:
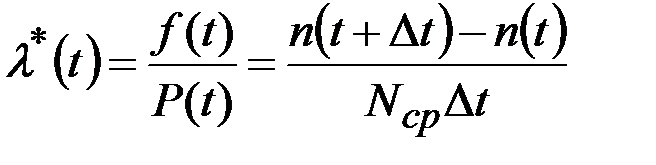 , (3.5)
, (3.5)
где 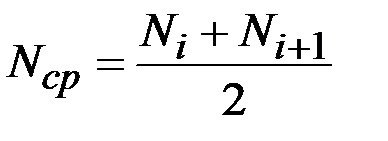 – среднее число изделий, исправно работающих в интервале
– среднее число изделий, исправно работающих в интервале 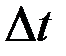 ;
; 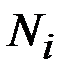 ,
, 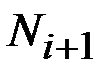 –соответственно число изделий, исправно работающих в конце интервала
–соответственно число изделий, исправно работающих в конце интервала 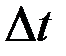 .
.
Интенсивность отказов является критерием, наиболее полно характеризующим надежность невосстанавливаемых объектов. Этот показатель характеризует надежность элемента в каждый данный момент времени, т.е. его локальную надежность. Интенсивность отказов связана однозначной зависимостью с вероятностью безотказной работы:
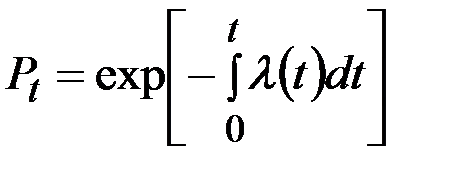 . (3.6)
. (3.6)
Средней наработкой до отказа называется математическое ожидание наработки объекта до первого отказа 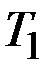 . Через вероятность безотказной работы наработка до отказа вычисляется следующим образом:
. Через вероятность безотказной работы наработка до отказа вычисляется следующим образом:
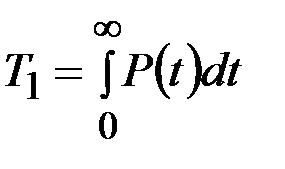 . (3.7)
. (3.7)
Статистическая оценка для средней наработки до отказа определяют по формуле:
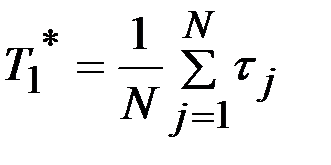 , (3.8)
, (3.8)
где 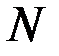 – число работоспособных объектов при
– число работоспособных объектов при 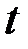 =0;
=0; 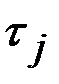 – наработка до первого отказа каждого из объектов.
– наработка до первого отказа каждого из объектов.
Для определения 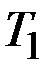 , необходимо знать время безотказной работа всех испытуемых изделий.
, необходимо знать время безотказной работа всех испытуемых изделий.
В теории надежности интенсивности отказов отводится особая роль, поскольку, зная интенсивность отказов отдельных элементов, можно выполнять расчеты показателей надежности при проектировании.
Тип распределения случайной величины нарабоки до отказа зависит от особенностей процесса развития отказа. Для электротехнических изделий, находящихся в эксплуатации, наиболее часто применяются следующие законы распределения: экспоненциальный, нормальный, Вейбулла. Ниже в табл. 3.2 приведены формулы для оценки показателей надежности при различных законах распределения наработки до отказа.
Из трех рассмотренных законов распределения случайной величины наиболее часто используется показательное распределение. Оно применимо для сложных систем, характеризует работу изделия на участке длительной эксплуатации, расчеты ведутся по простым формулам. При оценке надежности используются также нормальный закон распределения на участке ускоренного износа изделий и распределение Вейбулла на участке приработки.
Для описания дискретных случайных величин в теории надежности применяется распределение Пуассона. Согласно закону Пуассона вероятность того, что случайная величина примет вполне определенное значение 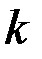 , вычисляется по формуле:
, вычисляется по формуле:
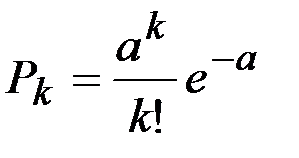 (3.9)
(3.9)
где 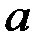 -параметр распределения.
-параметр распределения.
Таблица 3.2. Показатели надежности для различных законов распределения
| Тип распределения | Показатели надежности |
| Экспоненциальное | Вероятность безотказной работы: 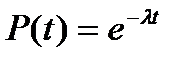 . Плотность распределения: . Плотность распределения: 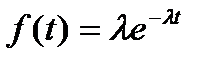 Интенсивность отказов: Интенсивность отказов: 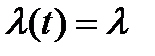 Наработка до отказа: Наработка до отказа: 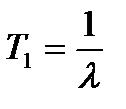 |
| Вейбула | Вероятность безотказной работы: 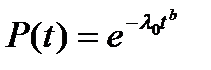 Плотность распределения: Плотность распределения: 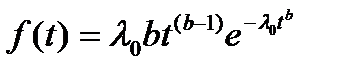 Интенсивность отказов: Интенсивность отказов: 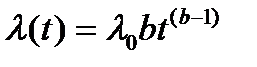 Наработка до отказа: Наработка до отказа: 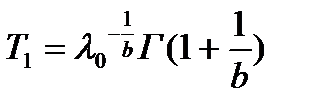 |
| Нормальное (усеченное t>0) | Вероятность безотказной работы: 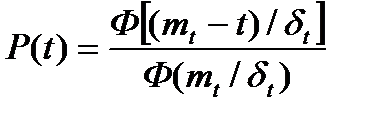 Плотность распределения: Плотность распределения:  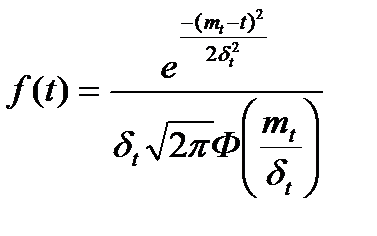 Интенсивность отказов: Интенсивность отказов: 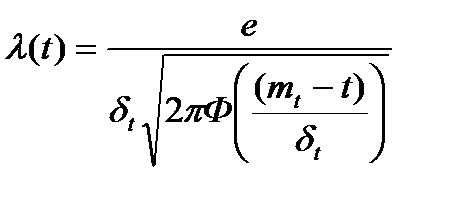 Наработка до отказа: Наработка до отказа: 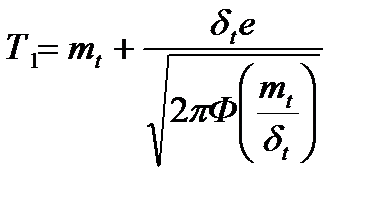 |
Примечание: 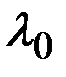 и
и 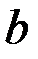 – параметры распределения Вейбула;
– параметры распределения Вейбула; 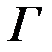 – гамма-функция (см. Приложение 1);
– гамма-функция (см. Приложение 1); 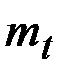 и
и 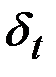 – параметры нормального распределения; Ф(х)=
– параметры нормального распределения; Ф(х)= 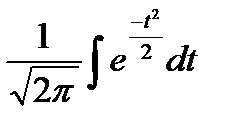 – функция Лапласа.
– функция Лапласа.
