Вычисление числовых характеристик распределения

После осуществления выборки дальнейшая работа с данными строится на принципе свёртки информации, т.е. получении числовых характеристик распределения. Для этого копируем на лист «Графика 2» таблицу 3 и создаем тут же следующую расчетную таблицу:

Таблица 4. Расчетная таблица для вычисления числовых характеристик

	mi	mi	-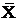
			-29,38	3452,738	-101441
37,5		37,5	-22,88	523,4944	-11977,6	274046,4
			-16,38	3219,653	-52737,9
50,5			-9,88	1561,83	-15430,9	152457,1
			-3,38	456,976	-1544,58	5220,677
63,5		2222,5	3,12	340,704	1062,996	3316,549
			9,62	2591,243	24927,76
76,5			16,12	2598,544	41888,53	675243,1
			22,62	2046,658	46295,39
Σ			-30,42	16791,84	-68957,7

Одной из основных характеристик распределения является тенденция наблюденных значений признака группироваться вокруг центра этого распределения. Эта характеристика называется центральной тенденцией.

Центральная тенденция обычно выражается тремя величинами:

1) средней величиной, именуемой средней арифметической выборки или выборочной средней;

2) средней величиной, именуемой медианой;

3) наиболее часто повторяющейся величиной, именуемой модой.

Эти величины также называют характеристиками положения, так как они показывают расположение полигона частот относительно оси абсцисс.

Когда ряд наблюденных значений хотят охарактеризовать одним значением, целесообразно бывает использовать выборочное среднее арифметическое .

Формула для определения выборочной средней на основе данных о распределении частот: , где

R – число интервалов разбиения (частичных интервалов),

- середина частичного интервала,

m_i – частота частичного интервала.

В нашем случае, как следует из таблицы 4, 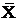= = 60,38.

Заметим, однако, что формулу можно применить для исходного статистического ряда таблицы 2. Здесь все m_i=1, а R=52. Тогда получим , что в точности совпадает с математическим ожиданием генеральной совокупности. Расхождение двух средних объясняется тем, что в результате группирования ряда из таблицы 2 в таблицу 3 происходит частичная потеря, искажение реальной статистической информации.

При некоторых формах распределения (речь идёт об эмпирическом распределении в отличие от теоретического распределения генеральной совокупности) хорошей характеристикой положения является медиана. К таким распределениям относятся распределения, обладающие значительной асимметрией или очень удлинёнными краями.

Медиана M_е представляет собой значение признака, которое делит пополам распределение всех наблюденных значений, то есть является той точкой, до и после которой лежит равное число наблюдений.

Формула определения медианы на основе распределения частот, т.е. для интервальных статистических рядов:

,

L – начало медианного интервала,

ΔХ – длина частичного интервала,

n_m-1 – накопленная частота предмедианного интервала,

m_m - частота медианного интервала.

Для интервального статистического ряда под модой М_о понимается значение признака в наиболее плотном, так называемом, модальном интервале.

Формула определения моды на основе распределения частот

М_о = ,

L – начало модального интервала,

m_m – частота модального интервала,

m_m-1 – частота предмодального интервала,

m_m+1 – частота постмодального интервала.

Для определения медианы интервального статистического ряда (таблица 3), по определению, необходимо выбрать интервал, в котором находится варианта, делящая ряд пополам. Это легко сделать, используя последний столбец (накопленные частоты). Медианным интервалом нашего ряда является интервал (60,25 ÷ 66,75). Значит,

60,62.

Значение моды

М_о= 53,75 + 6,5× = 59,13.

Рассмотренные выше числовые характеристики служат для описания распределения с точки зрения тенденции наблюденных значений признака группироваться вокруг некоторого их среднего значения. Наряду с этим всякое распределение характеризуется также рассеянием – отклонением значений наблюденного признака от его среднего значения. Для оценки варьирования (колеблемости) наблюденных значений будем пользоваться только стандартным отклонением.

Формула определения стандартного отклонения на основе распределения частот: . Для рассматриваемого интервального статистического ряда:

10,58.

Форма распределения описывается также с помощью характеристик, получивших название асимметрии и эксцесса.

Асимметрия, как явствует из названия, показывает, насколько несимметрично распределение, в то время как эксцесс характеризует островершинность или плосковершинность распределения (в точке максимальной частоты). Кривая может обладать большой крутизной и называться в этом случае островершинной, характеризоваться небольшой крутизной и называться плосковершинной или, наконец, иметь среднюю крутизну. Нормальная кривая обладает средней крутизной.

Коэффициент скошенности, или асимметрии, характеризует тенденцию к рассеянию в одном направлении больше, чем в другом.

Коэффициент относительной скошенности, или выборочный коэффициент асимметрии определяется для сгруппированных данных:

.

Разумеется, для симметричного распределения =0. Если значение меньше нуля, то большая часть ряда распределения располагается слева от оси, проходящей через варианту 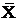параллельно оси ординат; если больше нуля, то справа от неё. В нашем случае = = - 0,388.

Эксцесс, напомним, характеризует островершинность распределения. Относительный эксцесс, или выборочный коэффициент эксцесса определяется: . Имеем: = – 3 = 0,32.

Для теоретического нормального распределения коэффициенты асимметрии и эксцесса равны нулю.

6. Оценка соответствия распределения выборочных частот

нормальному распределению

Вычислив на основе наших данных соответствующие им числовые характеристики, мы можем сопоставить полученные значения с параметрами нормально распределённой генеральной совокупности (табл. 5). Результаты такого сопоставления говорят о том, что фактические данные близки к теоретическим. Поскольку сопоставление основывалось на выборочных данных, естественно ожидать некоторого их расхождения с теоретическими.

Таблица 5. Функции результатов наблюдений и статистические

характеристики нормально распределённой генеральной совокупности

Выборочная совокупность	Генеральная совокупность
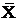	60,38	μ
	10,58	σ
	-0,388	α3
	00,32	α4-3

Для того, чтобы получить визуальное представление о степени соответствия нашей выборки нормальной кривой, воспользуемся гистограммой частот 150 изделий (рис.2) с наложенной на неё нормальной кривой с параметрами μ = 60 и σ = 10.

Вычисление ординат нормальной кривой выполнено в таблице 6 на листе «Графика 2». Увеличение числа интервалов (см. выделенную красным клетку в таблице) в нашем примере вызвано симметричностью нормальной кривой относительно μ (если μ =60, симметричная кривая будет иметь интервал 30÷90 или 0÷120, а наш ряд расположен в 31÷83) .

Значения в таблице 6 вычислены с использованием функции «=EXP(-t)»:

Величины получены умножением каждого из значений на . Умножение на (а не на ) необходимо для совмещения масштабов. Дело в том, что площадь гистограммы является суммой площадей прямоугольников с основанием ΔХ и равна 150*6,5=975. Но площадь под нормальной кривой, как это следует из свойства плотности распределения вероятностей, равна 1. Т.е. масштаб гистограммы равен .

Рабочую таблицу 6 создается на листе «Графика 2». Здесь же строится рисунок 4.

Таблица 6. Ординаты нормальной кривой (μ=60; σ=10)

	-29	-2,9	4,205	0,01492	0,580
37,5	-22,5	-2,25	2,53125	0,07956	3,095
	-16	-1,6	1,28	0,27804	10,815
50,5	-9,5	-0,95	0,45125	0,63683	24,771
	-3	-0,3	0,045	0,956	37,185
63,5	3,5	0,35	0,06125	0,94059	36,586
			0,5	0,60653	23,592
76,5	16,5	1,65	1,36125	0,25634	9,971
		2,3	2,645	0,07101	2,762
89,5	29,5	2,95	4,35125	0,01289	0,501

При рассмотрении рис.4 видим, что между нормальной кривой и гистограммой имеется несоответствие. Однако при этом следует помнить, что выборка содержит только 150 изделий, и наличие даже существенного расхождения не следует считать слишком неожиданным. Важнейшим показателем здесь является качественная схожесть и она имеется. Количественные же расхождения оцениваются средствами математической статистики.

Рис.4 Нормальная кривая и гистограмма

В таблице 7 приведено сравнение данных наблюдений с теоретическим распределением площади под нормальной кривой Гаусса.

Фактический процент наблюдений находится суммированием частот m_i статистического ряда (таблица 2), попадающих в заданные интервалы (см. клетки В58÷В63 таблицы 7 на листе «Графика 2»). Заносим эти суммы в клетки С58÷С63 таблицы 7 на листе «Графика 2».

Теоретический процент наблюдений находится с помощью функции НОРМСТРАСП (стандартное нормальное распределение):

Таблица 7. Сопоставление опытных данных с теоретическим

распределением площади под нормальной кривой

	Фактические наблюдения	Теоретическое распределение	Процент площади диапазона
z
	49,8		0,15865	0,68268949	73,33	68,27
70,96	0,84134
	39,22		0,02275	0,95449974	96,00	95,45
81,54	0,97724
	28,64		0,0013	0,9973002	100,00	99,73
92,12	0,9986

В нашем случае наблюдается хорошее согласие процентов наблюдений.

При необходимости можно выполнить дополнительную проверку соответствия распределения выборочных частот нормальному распределению. Для этого используется сравнение выборочной асимметрии А и выборочного эксцесса Е с теоретическими моментами нормального распределения.

Известно, что распределения указанных моментов являются асимптотически нормальными. На практике применяют критерий сравнения относительных выборочных моментов с и , с их стандартными ошибками:

и .

Если значения или оказываются меньше 2, это может расцениваться как подтверждение соответствия исследуемого выборочного распределения нормальному.

Вычисляем k-статистики Фишера, используя результаты вычислений из таблицы 4 (здесь , а :

60,38; 112,7;

k₃ = -469,1;

k₄ =

= 4729,4.

Следовательно, и

Сравним:

	-0,388		-0,392
	00,32		0,372

Проверяем значимость:

; =-1,98;

; 1,06

Для третьего выборочного момента критерий находится на границе допустимости, что соответствует визуальному сопоставлению опытной гистограммы и нормальной кривой (рис.4). Однако, поскольку ни одна из оценок более чем в два раза не превосходит свою стандартную ошибку, имеются все основания говорить о нормальности распределения изделий.