Отбор экспериментальных данных
Допустим, что для контроля изучаемого признака из генеральной совокупности выбираются по случайному закону 150 наблюдений (замеров).
Для симуляции такого отбора можно использовать равномерно распределенные случайные числа (РРСЧ). Переходим на вкладку «РРСЧ» и создаем, например, двести сорок пять пятизначных чисел.
Вводим необходимые сведения по схеме на следующем рисунке и выходной интервал курсором указываем в ячейке А2 листа РРСЧ.
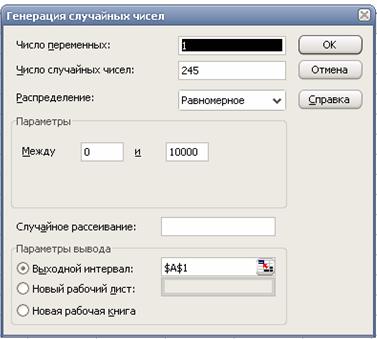
В результате наблюдаем в столбце А пятизначные случайные числа. Округляем их до целых в столбце С. Для этого в клетку С2 записываем функцию «=ЦЕЛОЕ(A2)»:
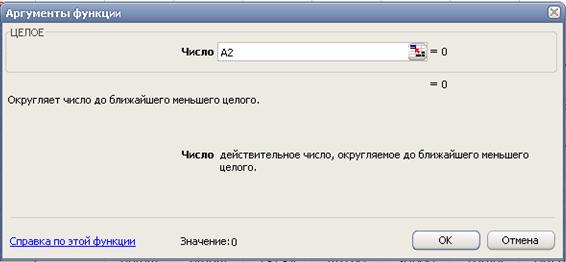
После ввода «ОК» клетка С2 выделена
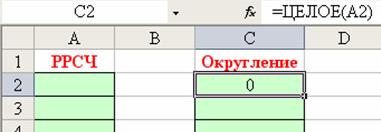
Установим курсор в выделенный нижний правый угол клетки (курсор должен принять вид знака «+») и, удерживая левую кнопку, «протягиваем» записанную функцию на все клетки столбца до С246.
Формируем рядом, последовательно по 35 чисел, «Таблицу РРСЧ» и копируем ее в файл отчета.
Таблица РРСЧ. Случайные пятизначные числа
Отбор 150 наблюдений (замеров) производим в следующем порядке:
1. Переходим на лист «Отбор» и копируем сюда в столбцы А и В, соответственно, РРСЧ и НРСВ:
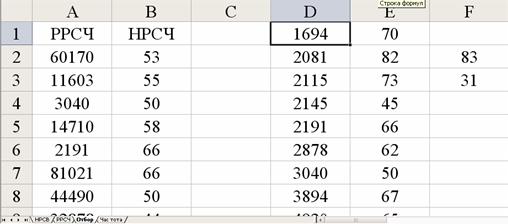
2. Столбцы симулированных распределений совместно сортируем по возрастанию РРСЧ.
3. Отбираем первые (или любым другим способом) 150 пар и копируем в столбцы D и E. Выбранные РРСЧ столбца D будем рассматривать как порядковые номера изделий из генеральной совокупности таблицы НРСВ и мы последовательно по 25 пар выписываем соответствующие им значения Хiпризнака Хв рабочую таблицу 1.
Таблица 1. Случайная выборка 150 значений признака
| РРСЧ | Хi | РРСЧ | Хi | РРСЧ | Хi | РРСЧ | Хi | РРСЧ | Хi | РРСЧ | Хi |
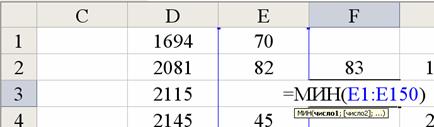
Экстремальные значения случайной выборки посредством встроенных функций «=МАКС(E1:E150)» и «=МИН(E1:E150)» вычисляем в столбце F (хmах =83 и хmin = 31):
3. Составление вариационного ряда по данным выборки
В том виде, в каком данные представлены в таблице 1, они мало пригодны для анализа. Больших результатов можно достичь при распределении частот наблюдаемого признака в порядке увеличения их численных значений (ранжирования данных).
Вычислим частоты данных с помощью функции «Частота» и получим вариационный ряд в виде расчетной таблицы 2. Для этого копируем на лист «Частота» от клетки А2 столбец E листа «Отбор». В столбце С листа «Частота» в диапазоне от хmin (=31) до хmах (=83) методом «протягивания» создаем столбик «Массив интервалов». Устанавливаем курсор в клетку D2 и выполняем схему по следующим рисункам:
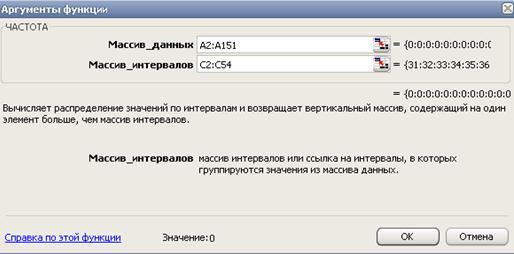
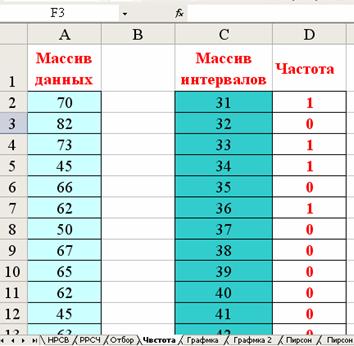
Результаты сводим в таблицу 2 и в файл отчета.
Таблица 2. Вариационный ряд наблюдений параметра
| Хi | mi | Хi | mi | Хi | mi | Хi | mi |
Полученная картина остаётся недостаточно наглядной для эффективного визуального анализа. Поэтому можно прибегнуть к соответствующей группировке данных, то есть разбиению всех значений признака Х из таблицы 2 на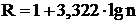 
(формула Стерджеса) интервалов длиной ∆Х = (хmах - хmin)/R, где n – объём выборки.
Вычисляем «=LOG10(150)»=2,176 и находим
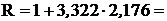8,229.
Если принять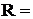 
8, то шаг будет ∆Х = (83-31)/8 ≈6,5. Задаем начало интервалов как 
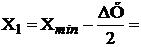31-3,25=27,75 и разбиваем все значения НРСВ Х из таблицы 2 уже на 
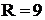интервалов (групп) длиной ∆Х=6,5 каждый, причём правая граница предыдущего интервала служит левой границей следующего. Получаем частичные интервалы по схеме:
Х1 ÷ Х1 + ∆Х = Х2, Х2 ÷ Х2 + ∆Х = Х3, … Х9 ÷ Х9 + ∆Х = Х10.
Основную часть таблицы 3 создаем на листе «Частота»:
Таблица 3. Сгруппированное распределение частот
| Интервальный ряд распределения | |||
| Интервал | Центр интервала | Частота | Накопленная частота |
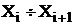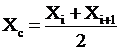 |  | mi | nX |
| 27,75 ÷ 34,25 | |||
| 34,25 ÷ 40,75 | 37,5 | ||
| 40,75 ÷ 47,25 | |||
| 47,25 ÷ 53,75 | 50,5 | ||
| 53,75 ÷ 60,25 | |||
| 60,25 ÷ 66,75 | 63,5 | ||
| 66,75 ÷ 73,25 | |||
| 73,25 ÷ 79,75 | 76,5 | ||
| 79,75 ÷ 86,25 | |||
| Сумма | - |