Предельные теоремы теории вероятностей

Центральная предельная теорема (ЦПТ) ( в формулировке Ляпунова А.М. для одинаково распределенных СВ). Если попарно независимые СВ X₁, X₂, ..., X_n, ... имеют одинаковый закон распределения с конечными числовыми характеристиками M[X_i] = m и D[X_i] = s², то при n ® ¥ закон распределения СВ 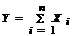неограниченно приближается к нормальному закону N(n×m, ).

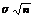Следствие. Если в условии теоремы СВ 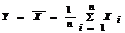, то при n ® ¥ закон распределения СВ Y неограниченно приближается к нормальному закону N(m, s/ ).

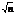Теорема Муавра-Лапласа.Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Тогда при n ® ¥ и фиксированном значении вероятности “успеха” в одном испытании p закон распределения СВ K неограниченно приближается к нормальному закону N(n×p, ).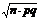

3 Пусть СВ X_i подчиняется закону распределения Бернулли, следовательно M[X_i] = p и D[X_i] = s² = p×q. Так как согласно ЦПТ при n ® ¥ и фиксированном значении p закон распределения СВ 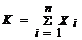неограниченно приближается к нормальному закону N(n× p, 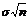), что и требовалось показать. 4

Следствие. Если в условии теоремы вместо СВ К рассмотреть СВ К/n - частоту “успехов” в n испытаниях по схеме Бернулли, то ее закон распределения при n ® ¥ и фиксированном значении p неограниченно приближается к нормальному закону N(p, ).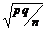

Замечание. Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Законом распределения такой СВ является биноминальный закон. Тогда при n ® ¥ биноминальный закон имеет два предельных распределения:

n распределение Пуассона (при n ® ¥ и l = n×p = const);

n распределение Гаусса N(n×p, 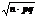) (при n ® ¥ и p = const).

Пример. Вероятность “успеха” в одном испытании всего лишь p = 0,8. Сколько нужно провести испытаний, чтобы с вероятностью не менее 0,9 можно ожидать, что наблюдаемая частота “успеха” в испытаниях по схеме Бернулли отклонится от вероятности p не более чем на e = 0,01?

Решение. Для сравнения решим задачу двумя способами:

а) На основе второго неравенства Чебышева имеем:

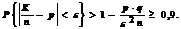Следовательно: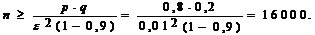

б) Используя теорему Муавра-Лапласа и учитывая, что если СВ Y ~N(m, s), то 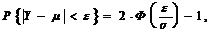получаем:

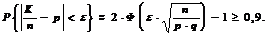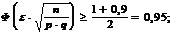
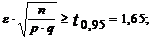
Следовательно: 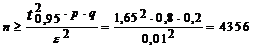, т.е. почти в четыре раза меньше.

При этом полученное значение настолько велико, что погрешностью используемой формулы можно пренебречь.

Задача 2. По полосе укреплений противника осуществляется залп из 100 орудий. При стрельбе из одного такого орудия математическое ожидание числа попаданий равно 2, а среднеквадратическое отклонение числа попаданий равно 1,5. Найти приближенно вероятность того, что в полосу укреплений противника попадет от 180 до 220 снарядов.

Задача 3. Противник атакует полосу укреплений, используя в наступлении 50 танков. Вероятность вывода из строя танка в этом бою равна 0,4. Если выведено из строя не менее 35% танков, то противник прекращает свое наступление. Требуется найти вероятность того, что противник откажется от наступления.

Точечные оценки параметров

Статистикой называется любая функция выборочных значений x₁, x₂, ... x_n: G = G(x₁, x₂, ... x_n).

Точечной оценкой Q неизвестного параметра J называется любая статистика G = G(X₁, X₂, ... X_n), распределение которой сосредоточено вблизи неизвестного значения J. Критерии качества оценок:

Несмещенность. Оценка Q называется несмещенной оценкой J, если M[Q] = J.

Состоятельность. Оценка Q называется состоятельной, если она становится все более точной с ростом объема выборки n, т.е.:

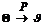при n ® ¥ или для любого e > 0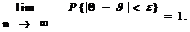

Эффективность. Оценка Q называется эффективной среди оценок Q_i, если ее дисперсия является наименьшей среди всех дисперсий этих оценок Q_i.

Точечные оценки M[X], D[X] и их свойства

Утверждение 1. Точечная оценка 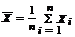параметра M[X], является несмещенной, состоятельной и эффективной в классе всех линейных оценок вида: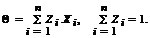

3 Так как X_i являются независимыми СВ, закон распределения которых совпадает с законом распределения СВ X, т.е. M[X] = M[X_i], D[X] = D[X_i]. Тогда, используя свойства математического ожидания и дисперсии имеем:

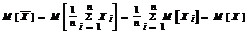, т.е. несмещенность доказана.

Из следствия закона больших чисел в форме Чебышева очевидно, что 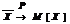при n ® ¥ или для любого e > 0 справедливо

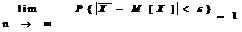, т.е. состоятельность оценки доказана.

Покажем, что точечная оценка является эффективной в классе всех линейных оценок вида: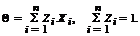

Имеем 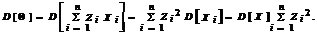Определим значения Z_i, при которых функция 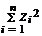принимает минимальное значение при условии 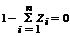. Для нахождения условного экстремума составим функцию Лагранжа

,

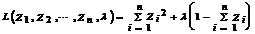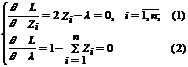тогда необходимые условия минимума функции Лагранжа определяет система из уравнений (1) и (2). Из уравнения (1) для i = 1,2, ..., n получаем Zi = l/2. Из уравнения (2) следует l = 2/n. Тогда Zi = 1/n для i = 1,2, ..., n, что и требовалось показать. 4

Утверждение 2. Точечная оценка 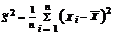параметра D[X], является смещенной так как .

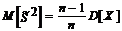Утверждение 3. Точечная оценка 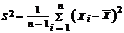параметра D[X], является несмещенной, состоятельной и эффективной в классе всех квадратичных оценок вида: