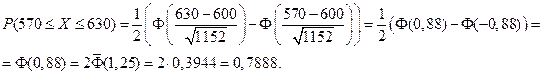Предельные теоремы теории вероятностей
Выше отмечалось, что при достаточно большом количестве испытаний, поставленных в одинаковых условиях, характеристики случайных событий и случайных величин становятся почти неслучайными. Это позволяет использовать результаты наблюдений случайных событий для предсказания исхода того или иного опыта.
Предельные теоремы теории вероятностей устанавливают соответствие между теоретическими и экспериментальными характеристиками случайных величин при большом количестве испытаний.
Рассмотрим задачу нахождения предельного закона распределения суммы:
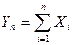
когда число слагаемых п неограниченно возрастает. Эту задачу решает Центральная предельная теорема Ляпунова.
В зависимости от условий распределения случайных величин 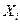 , образующих сумму, возможны различные формулировки центральной предельной теоремы.
, образующих сумму, возможны различные формулировки центральной предельной теоремы.
Допустим, что случайные величины 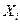 взаимно независимы и одинаково распределены.
взаимно независимы и одинаково распределены.
Теорема Ляпунова. Если случайные величины 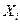 взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием т и дисперсией
взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием т и дисперсией 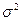 , причем существует третий абсолютный момент
, причем существует третий абсолютный момент 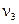 , то при неограниченном увеличении числа испытаний п закон распределения суммы
, то при неограниченном увеличении числа испытаний п закон распределения суммы 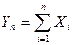 неограниченно приближается к нормальному.
неограниченно приближается к нормальному.
При доказательстве теоремы Ляпуновым используются так называемые характеристические функции.
Определение.Характеристической функцией случайной величины Х называется функция
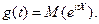
Эта функция представляет собой математическое ожидание некоторой комплексной случайной величины 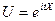 , являющейся функцией от случайной величины Х. При решении многих задач удобнее пользоваться характеристическими функциями, а не законами распределения.
, являющейся функцией от случайной величины Х. При решении многих задач удобнее пользоваться характеристическими функциями, а не законами распределения.
Зная закон распределения, можно найти характеристическую функцию по формуле (для непрерывных случайных величин):
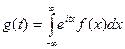 .
.
Очевидно, данная формула представляет собой преобразование Фурье для функции плотности распределения. С помощью обратного преобразования Фурье можно по характеристической функции найти закон распределения.
Введение характеристических функций позволяет упростить операции с числовыми характеристиками случайных величин.
В случае нормального распределения характеристическая функция имеет вид:
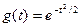 .
.
Сформулируем некоторые свойства характеристических функций:
1) Если случайные величины Х и Y связаны соотношением:
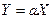 ,
,
где а – неслучайный множитель, то
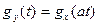 .
.
2) Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.
Случайные величины 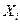 , рассмотренные в центральной предельной теореме, могут обладать произвольными распределениями вероятностей.
, рассмотренные в центральной предельной теореме, могут обладать произвольными распределениями вероятностей.
Если все эти случайные величины одинаково распределены, дискретны и принимают только два возможных значения 0 или 1, то получается простейший следующей случай центральной предельной теоремы.
Теорема Муавра – Лапласа. Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то для любого интервала 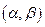 справедливо соотношение:
справедливо соотношение:
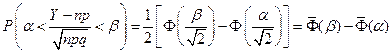 ,
,
где Y – число появлений события А в п опытах, 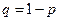 ,
, 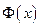 – функция Лапласа,
– функция Лапласа, 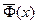 - нормированная функция Лапласа .
- нормированная функция Лапласа .
Теорема Муавра – Лапласа описывает поведение биноминального распределения при больших значениях п.
Данная теорема позволяет существенно упростить вычисление по формуле биноминального распределения.
Расчет вероятности попадания значения случайной величины в заданный интервал 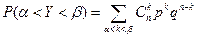 при больших значениях п крайне затруднителен. В этом случае используют формулу:
при больших значениях п крайне затруднителен. В этом случае используют формулу:
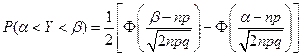 .
.
Теорема Муавра – Лапласа широко применяется при решении практических задач.
Пример. Вероятность наступления события А в каждом испытании равна 0,3. Используя неравенство Чебышева, оценить вероятность того, что в 10000 испытаниях отклонение относительной частоты появления события А от его вероятности не превзойдет по абсолютной величине 0,01.
В соответствии с неравенством Чебышева вероятность того, что отклонение случайной величины от ее математического ожидания будет меньше некоторого числа e, ограничена в соответствии с неравенством 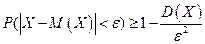 .
.
Определить математическое ожидание и дисперсию числа появления события А при одном опыте. Для события А случайная величина может принимать одно из двух значений: 1- событие появилось, 0- событие не появилось. При этом вероятность значения 1 равна вероятности р=0,3, а вероятность значения 0- равна вероятности ненаступления события А:
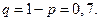
По определению математического ожидания имеем:
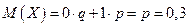 .
.
Дисперсия: 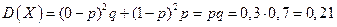 .
.
В случае п независимых испытаний получаем 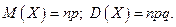
В нашем случае получаем: 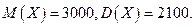
Вероятность отклонения относительной частоты появления события А в п испытаниях от вероятности на величину, не превышающую 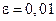 равна:
равна:
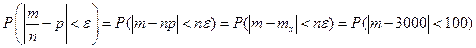 .
.
Выражение полученное в результате этих простых преобразований представляет собой вероятность отклонения числа т появления события А от математического ожидания на величину не большую, чем 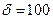 .
.
В соответствии с неравенством Чебышева эта вероятность будет не меньше, чем величина 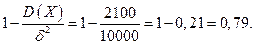
Пример. Сколько следует проверить деталей, чтобы с вероятностью, не меньшей 0,96, можно было ожидать, что абсолютная величина отклонения относительной частоты годных деталей от вероятности детали быть годной, равной 0,98, не превысит 0,02.
Условие задачи фактически означает, что выполняется неравенство:
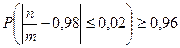 .
.
Здесь п- число годных деталей, т- число проверенных деталей. Для применения неравенства Чебышева преобразуем полученное выражение:
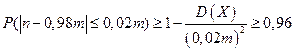 .
.
Домножая выражение, стоящего в скобках, на т получаем вероятность отклонения по модулю количества годных деталей от своего математического ожидания, следовательно, можно применить неравенство Чебышева, т.е. эта вероятность должна быть не меньше, чем величина 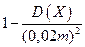 , а по условию задачи еще и не меньше, чем 0,96.
, а по условию задачи еще и не меньше, чем 0,96.
Таким образом, получаем неравенство 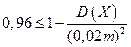 . Как уже говорилось в предыдущей задаче, дисперсия может быть найдена по формуле
. Как уже говорилось в предыдущей задаче, дисперсия может быть найдена по формуле 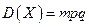 .
.
Таким образом, получаем:
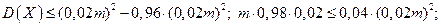
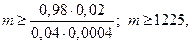
т.е. для выполнения требуемых условий необходимо не менее 1225 деталей.
Пример. Суточная потребность электроэнергии в населенном пункте является случайной величиной, математическое ожидание которой равно 3000 кВт/час, а дисперсия составляет 2500. Оценить вероятность того, что в ближайшие сутки расход электроэнергии в этом населенном пункте будет от 2500 до 3500 кВт/час.
Требуется найти вероятность попадания случайной величины в заданный интервал:
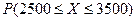 .
.
Крайние значения интервала отклоняются от математического ожидания на одну и ту же величину, а именно – на 500. Тогда можно записать с учетом неравенства Чебышева:
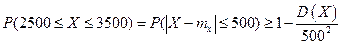 .
.
Отсюда получаем:
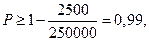
т.е. искомая вероятность будет не меньше, чем 0,99.
Пример. Среднее квадратическое отклонение каждой из 2500 независимых случайных величин не превосходит 3. Оценить вероятность того, что абсолютная величина отклонения среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превосходит 0,3. Найти вероятность:
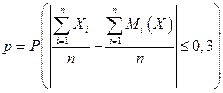 .
.
Неравенство Чебышева в случае суммы случайных величин имеет вид:
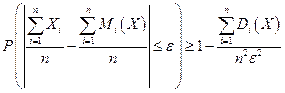 .
.
Если среднее квадратическое отклонение не превосходит 3, то, очевидно, дисперсия не превосходит 9. Величина 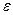 по условию задачи равна 0,3.
по условию задачи равна 0,3.
Тогда 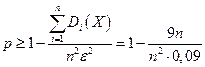 . Отсюда получаем при
. Отсюда получаем при 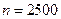 :
: 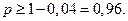
Пример. Выборочным путем требуется определить среднюю длину изготавливаемых деталей. Сколько нужно исследовать деталей, чтобы с вероятностью, большей чем 0,9, можно было утверждать, что средняя длина отобранных изделий будет отличаться от математического ожидания этого среднего (средняя длина деталей всей партии) не более, чем на 0,001 см.? Установлено, что среднее квадратическое отклонение длины детали не превышает 0,04 см.
По условию если среднее квадратическое отклонение не превышает 0,04, то дисперсия, очевидно, не превышает (0,04)2. Также по условию дано, что
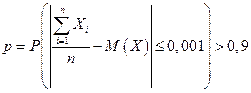 .
.
Если преобразовать соотношение, стоящее в скобках и после этого применить неравенство Чебышева, получаем:
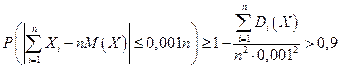 ;
;
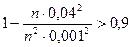 ;
; 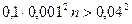 ;
; 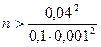 ;
; 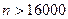 .
.
Т.е. для достижения требуемой вероятности необходимо отобрать более 16000 деталей.
Пример. Вероятность того, что наудачу выбранная деталь окажется бракованной, при каждой проверке одна и та же и равна 0,2. Определить вероятность того, что среди 50 наугад выбранных деталей бракованных окажется не менее 6.
Для того, чтобы воспользоваться теоремой Муавра - Лапласа найдем математическое ожидание и дисперсию количества бракованных деталей в 50 – ти отобранных:
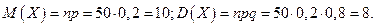
Фактически в задаче требуется определить вероятность того, что бракованных деталей будет не менее шести, но и, очевидно, не более 50:
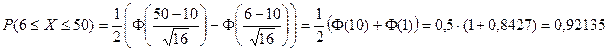 .
.
Значения функции Лапласа находятся по таблице. Хотя значения функции Лапласа 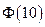 в таблице нет, но т.к. в таблицах указано, что
в таблице нет, но т.к. в таблицах указано, что 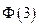 =1,0000, то все значения от величин, превышающих 3 также равны 1.
=1,0000, то все значения от величин, превышающих 3 также равны 1.
Пример. Известно, что 60% всего числа изготавливаемых заводом изделий являются изделиями первого сорта. Приемщик берет первые попавшиеся 200 изделий. Чему равна вероятность того, что среди них окажется из от 120 до 150 изделий первого сорта?
Вероятность того, что деталь окажется первого сорта, равна, очевидно, 0,6.
Математическое ожидание числа изделий первого сорта равно:
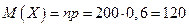 .
.
По теореме Муавра - Лапласа получаем:
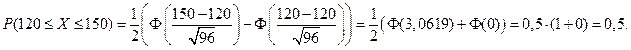 Пример. Проверкой установлено, что 96% изделий служат не меньше гарантируемого срока. Наугад выбирают 15000 изделий. Найти вероятность того, что со сроком службы менее гарантируемого будет от 570 до 630 изделий.
Пример. Проверкой установлено, что 96% изделий служат не меньше гарантируемого срока. Наугад выбирают 15000 изделий. Найти вероятность того, что со сроком службы менее гарантируемого будет от 570 до 630 изделий.
Вероятность того, что срок службы изделия будет менее гарантированного равна:
1 – 0,96 = 0,04.
Математическое ожидание числа таких изделий равно 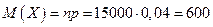 .По теореме Муавра - Лапласа получаем:
.По теореме Муавра - Лапласа получаем: