ЭС с запоминанием экстремума

Структура системы с запоминанием экстремума представлена на рис. 2.25.

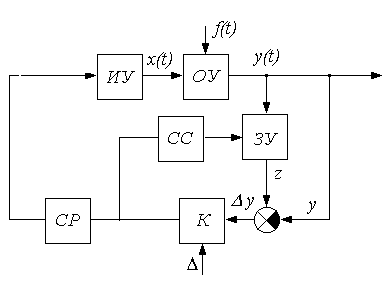
Рис. 2.25. Структура экстремальной системы с запоминанием экстремума

Она включает:

ЗУ – запоминающее устройство,

К – компаратор,

СР – схема реверса,

ИУ – исполняющее устройство,

СС – схема сброса.

Временные диаграммы функционирования экстремальной системы с запоминающим устройством, работающим по алгоритму

,

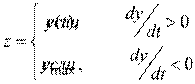представлены на рис. 2.26,2.27.

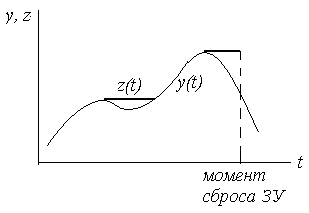
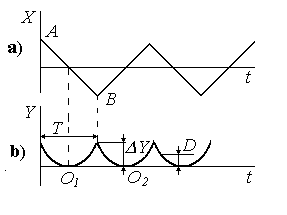
Рис. 2.26. Графики изменения основных переменных, характеризующих процесс в экстремальной системе с запоминанием экстремума

Данная система является релейной

Многомерные ЭС

Многомерные ЭС предполагают наличие объекта управления с экстремальной характеристикой, состояние которого зависит от нескольких входных переменных. На рис. 2.27 показана общая структура многомерных ЭС.

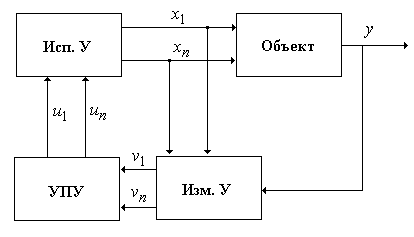
Рис. 2.27. Структура многомерной ЭС

Особенности данной системы связаны с блоками УПУ и Изм.У.

Пусть имеем зависимость 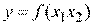. Изобразим 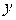на плоскости линиями уровня для значений …

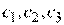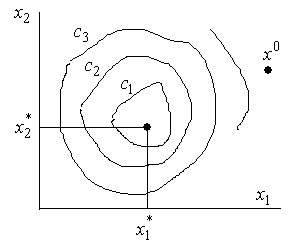
Рис. 2.28 Постановка задачи двумерного экстремального поиска

Пусть начальная точка состояния системы соответствует 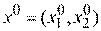. Алгоритм поиска может быть следующим.

: а) получить информацию о поведении функции в окрестности рабочей точки;

б) организовать движение системы (формулирование управляющих воздействий) в требуемом направлении.

Методы поиска экстремума функции многих переменных

Методы поиска экстремума функции многих переменных, наиболее часто используемые в экстремальных системах управления, можно разделить на две группы:

а) детерминированные,

б) случайного поиска.

Градиентные методы

Среди детерминированных способов наиболее эффективными в системах адаптивного управления являются градиентные методы. Градиентные методы основаны на использовании градиента целевой функции. Указанные методы носят итеративный характер, так как компоненты градиента являются, как правило, нелинейными функциями управляемых переменных.

Основная идея всех градиентных методов состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, которое определяется антиградиентом. Эта идея может реализоваться, например, следующим образом.

Выберем каким-либо способом начальную точку, вычислим в ней градиент рассматриваемой функции и сделаем небольшой шаг в обратном, антиградиентном направлении. В результате мы придем в точку, в которой значение функции будет меньше первоначального. В новой точке повторим процедуру: снова вычислим градиент функции и сделаем шаг в обратном направлении. Продолжая этот процесс, мы будем двигаться в сторону убывания функции.

Наглядной интерпретацией задачи градиентного спуска можно считать положение человека, который хочет максимально быстро спуститься на дно котловины, заросшей лесом, но видит перед собой лишь ограниченный участок местности. В такой ситуации логичным алгоритмом действия является движение в ту сторону, где местность наиболее круто идет вниз, т.е. в сторону антиградиента функции высоты.

Далее везде будем предполагать, что 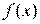, 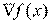существуют и непрерывны. Предполагается, что компоненты градиента могут быть записаны в аналитическом виде или с достаточно высокой точностью вычислены при помощи численных методов.

Замечание. В практических задачах найти значения производных целевых функций вида 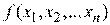аналитически, как правило, не удается и их вычисляют приближенно:

.

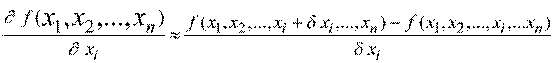Выбор величин приращений по координатам 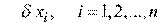зависит от возможностей используемой ЭВМ и необходимой точности вычислений.

Все градиентные методы поиска минимума основаны на итерационной процедуре, реализуемой в соответствии с формулой

,

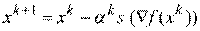где 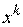– текущее приближение к решению ;

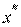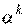– параметр, регулирующий длину 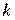-го шага;

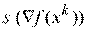– направление поиска в 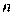- мерном пространстве управляемых переменных , .

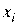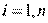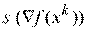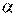Способ определения и на каждой итерации связан с особенностями применяемого метода.

Ранее уже отмечалось, что градиент функции 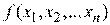в точке 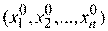− это вектор

,

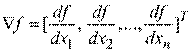проекции которого являются производными по координатам и вычислены для 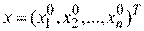. Длина вектора градиента

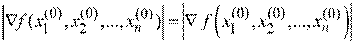(2.1)

характеризует скорость возрастания функции в этой точке, а направление соответствует направлению быстрейшего возрастания функции. Антиградиент - это вектор такой же длины, направленный в противоположную сторону (рис. 2.29). В точке минимума градиент функции равен нулю.

Единичный вектор градиента определяется как

.

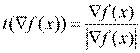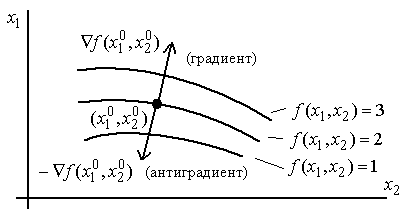
Рис. 2.29. Градиент и антиградиент функции

При поиске минимума каждая следующая точка поиска 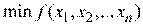(каждый новый член минимизирующей последовательности) получается в результате перемещения из предыдущей точки по направлению антиградиента целевой функции по формуле

.

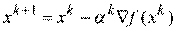Если в результате этого перемещения наблюдается увеличение значения целевой функции, то значение рабочего шага поиска уменьшается. Поиск прекращается, когда выполняется необходимое условие 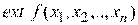, например, длина вектора градиента становится меньше требуемой точности:

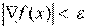. (2.2)

Различают методы градиента с переменным шагом и с постоянным шагом (рис. 2.30). При использовании метода градиента с переменным шагом изменение значений 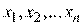производится согласно выражению

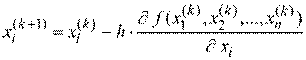, i=1,2,...,n , k=0,1,2…, (2.3)

а останов поиска - при выполнении неравенства (2.2). При возникновении ситуации 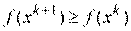значение параметра h уменьшается, например, делится на число 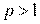. Характер изменения значений 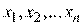, согласно (2.3), зависит от величины и знака соответствующих частных производных целевой функции.

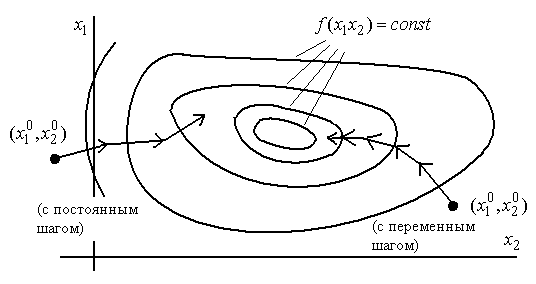
Рис. 2.30. Методы с постоянным и переменным шагом

К недостаткам метода можно отнести то, что, во-первых, на каждом шаге необходимо определять значение градиента. Это может быть не просто, если градиент определяется экспериментально. Во-вторых, по мере приближения к точке 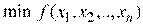абсолютные величины частных производных уменьшаются, следовательно, и шаг поиска является переменным – уменьшается по мере приближения к искомой точке. Такой характер поиска 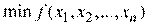требует иногда весьма значительных затрат времени.

Второй из отмеченных недостатков может быть устранен применением метода градиента с постоянным шагом. Метод позволяет сократить затраты времени, но требует несколько большего объема вычислений при изменении значений аргументов целевой функции. Его основное соотношение:

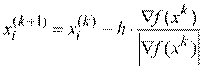, i=1,2,...,n; k=0,1,2,... . (2.4)

Метод использует вектор градиента единичной длины, который определяет лишь направление градиента, поэтому движение по 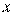осуществляется с постоянной скоростью, зависящей от величины шага 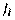. Если изменение аргументов целевой функции в соответствии с (2.4) приводит к увеличению ее значения, параметр поиска 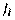уменьшается. Останов поиска 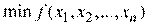по методу градиента с постоянным шагом осуществляется при выполнении неравенства .

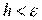Метод Коши (Наискорейшего спуска)

Вычисление градиента на каждом шаге, позволяющее все время двигаться в направлении наиболее быстрого убывания целевой функции, может в то же время замедлить вычислительный процесс. Дело в том, что подсчет градиента - обычно гораздо более сложная операция, чем подсчет самой функции, особенно если аналитическое выражение градиента отсутствует. Поэтому часто пользуются модификацией градиентного метода, получившей название метода наискорейшего спуска или метода Коши (рис.2.31).

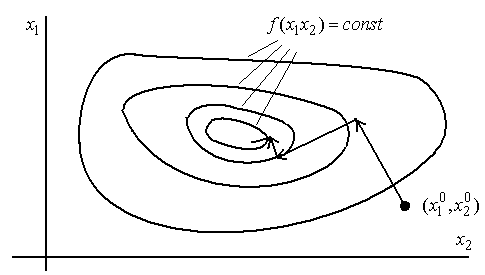
Рис. 2.31. Иллюстрация к методу наискорейшего спуска

Согласно этому методу после вычисления градиента функции в начальной точке делают в направлении антиградиента не маленький шаг, а движутся до тех пор, пока функция убывает. Достигнув точки минимума на выбранном направлении, снова вычисляют градиент функции и повторяют описанную процедуру. При этом градиент вычисляется гораздо реже, только при смене направлений движения.

Хотя траектория ведет к цели не так быстро, как на рис. 2.30, экономия машинного времени за счет более редкого вычисления градиента может быть весьма существенной.

Метод может быть реализован в нескольких вариантах. Простейшим является использование формулы

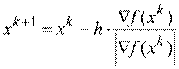
для последовательного движения к экстремуму, пока будет выполняться условие 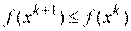. Нарушение данного условия означает прохождение точки минимума и говорит о том, что необходимо изменить направление движения. В достигнутой точке производится новый расчет вектора градиента и процесс повторяется.

Другой вариант состоит в том, что значение шага оптимизации 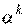вычисляется путем решения задачи минимизации 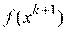вдоль направления 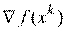с помощью того или иного метода одномерного поиска. Этот вариант реализации алгоритма более сложный, но обычно требует меньшего количества итераций.

Пусть функция 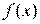дифференцируема по 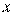и вектор градиента может быть записан аналитически. Тогда поиск минимума функции с использованием процедуры одномерной минимизации включает следующие этапы.

Этап 1. Определение аналитических соотношений для вычисления градиента функции 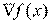, длины вектора градиента 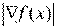и единичного вектора градиента .

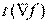Этап 2. Выбор исходной точк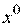и при 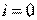(начальных значений аргументов функции).

Этап 3. Выбор шага a изменения координат текущей точки 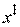. Осуществляется из условия достижения экстремума функции 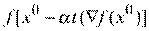одного аргумента 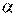в соответствии с уравнением

.

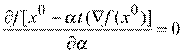Корень этого уравнения, соответствующий минимуму функции 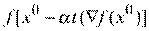, обозначим .

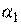Этап 4. Следующее приближение 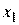вычисляется по формуле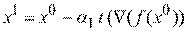

Этап 5. Производится возврат к этапу 3.

В результате формируется последовательность приближений 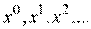. Вычислительный процесс заканчивается, когда будет достигнута точка 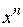, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми).

Пример. Выполнить шаг наискорейшего спуска для функции вида

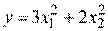
Решение.

Этап 1. Общий вид градиента функции :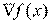

, ,

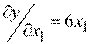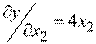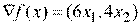
Длина вектора градиента:

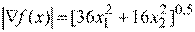
Этап 2. Выбор начальной точки, например .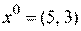

Этап 3. Вычисление координат единичного вектора градиента

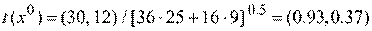
Координаты точки 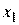при движении по направлению вектора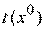

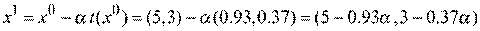
Запишем выражение для функции у в точке 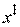как функцию от :

.

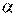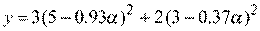Этап 4. Выбор шага а изменения координат текущей точки. Найдя производную от 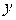по 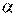в точке 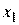и приравняв ее к нулю получим 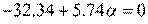. Следовательно, шаг .

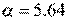Этап 5. Делаем шаг в направлении антиградиента. Координаты точки 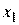после выполнения первого шага наискорейшего спуска по формуле

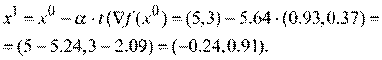
Аналогично выполняется следующий шаг наискорейшего спуска.

Рассмотренный алгоритм применяют только для нелинейныхфункций. Если функция отклика является линейной, то выбор оптимального значения параметра a невозможен. В этом случае шаг выбирается исходя из эвристических предположений исследователя о виде функции отклика.