Пространство элементарных исходов. Алгебра событий

Пространством элементарных исходов 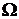(«омега») называется множество, содержащее все возможные результаты данного случайного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой 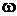(«омега») с индексами или без.

Событиями мы будем называть подмножества множества 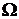. Говорят, что в результате эксперимента произошло событие А Í 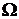, если в эксперименте произошел один из элементарных исходов, входящих в множество А. События обозначаются, как правило, заглавными буквами латинского алфавита: .

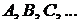Пример 1. Один раз подбрасывается одна игральная кость (кубик). Самый разумный способ задать пространство элементарных исходов таков:

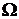= {1,2,3,4,5,6}, элементарные исходы здесь соответствуют числу выпавших очков.

Примеры событий: A = {1,2} — выпало одно или два очка; A = {1,3,5} — выпало нечетное число очков.

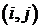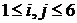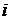Пример 2. Два раза подбрасывается одна игральная кость (кубик). Или, что, то же самое, один раз подбрасываются две игральные кости. Здесь самый разумный способ задать пространство элементарных исходов — считать результатом эксперимента упорядоченную пару чисел , в которой и – число очков, выпавших первый раз, 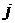– число очков, выпавших второй раз. = .

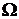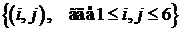Примеры событий:

A = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)} — при первом подбрасывании выпало одно очко;

A = {(1,1),(2,2), (3,3), (4,4), (5,5), (6,6)} — при двух подбрасываниях выпало одинаковое число очков.

Пример 3. Монета подбрасывается до тех пор, пока не выпадет вверх гербом. Пространство элементарных исходов состоит из бесконечного, но счетного числа исходов:

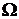= {г, рг, ррг, рррг, ррррг, рррррг, …} , где р и г обозначают выпадение решки и герба при одном подбрасывании, соответственно.

Достоверным называется событие, которое обязательно происходит в результате эксперимента, это единственное событие, включающее все без исключения элементарные исходы — событие 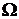(пространство элементарных исходов).

Невозможным называется событие, которое не может произойти в результате эксперимента, то есть событие, не содержащее ни одного элементарного исхода («пустое множество» Æ). Заметим, что всегда Æ Î .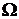

Несколько событий в данном опыте называются равновозможными, если не одно из них не является объективно более возможным, чем другие, т.е. все события имеют равные «шансы». Например, выпадение герба или решки при бросании монеты – равновозможные события.

Пусть 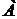и 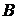— события.

Объединением 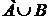событи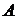й и 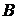называется событие, состоящее в том, что произошло либо 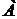, либо 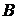, либо оба события одновременно. 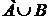есть множество, содержащее как элементарные исходы, входящие в 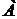, так и элементарные исходы, входящие в .

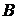Произведением 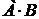событи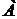й и 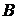называется событие 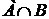, состоящее в том, что произошли оба события 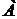и 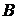одновременно. То есть 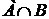есть множество, содержащее элементарные исходы, входящие одновременно 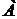и в ,и в .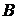

Дополнением 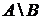события 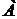до 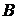называется событие, состоящее в том, что произошло событие 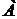, но не произошло В. То есть 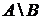есть множество, содержащее элементарные исходы, входящие в 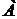, но не входящие в .

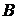Противоположным (или дополнительным) к событию 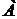называется событие 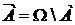, состоящее в том, что событие 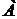в результате эксперимента не произошло. Иначе говоря, 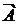есть множество, содержащее элементарные исходы, не входящие в .

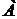События 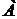и 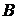называются несовместными, если 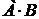= Æ.

События А₁, А₂ , … А_n называются попарно несовместными, если для любых 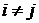, , 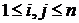события 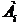и 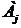несовместны.

Замечание. Понятия суммы и произведения событий переносятся на бесконечные последовательности событий:

, .

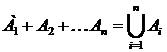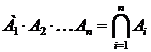Свойства алгебры событий

1. 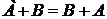– коммутативность

2. 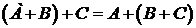– ассоциативность

3. 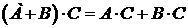– дистрибутивность

4. ,

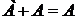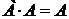
5. ,

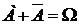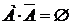
6. ,

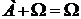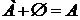
7. ,

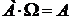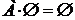
8. ,

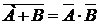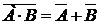
Пример. По мишени производится три выстрела. 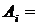{попадание при 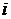-том выстреле}, 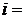1, 2, 3.

Представить в виде сумм, произведений или сумм произведений событи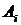й и 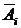следующие события:

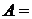{все три попадания};

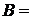{все три промаха};

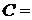{хотя бы одно попадание};

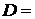{хотя бы один промах};

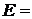{не менее двух попаданий};

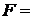{не более одного попадания}.

Решение. Противоположным событию 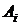будет событие 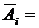{промах при 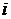-том выстреле}, 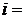1, 2, 3. Тогда,

;

;

;

;

;

;
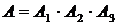
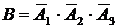
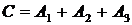
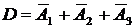
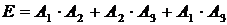
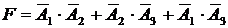