Математические методы теории оптимизации.
Задача о рационе.
Фермер имеет в своем распоряжении n-видов кормов для кормления домашних животных, каждый из которых содержит m-видов различных питательных веществ. Известно, что единица каждого вида кормов содержит определенное количество единиц каждого вида питательных веществ и имеет конкретную стоимость.
Требуется составить такой рацион, который бы удовлетворял потребность во всех питательных веществах, и имел бы наименьшую стоимость.
Транспортная задача.
Определить оптимального план перевозок однородного продукта из пунктов отправления в пункты назначения при известных тарифах, запасах в пунктах отправления и потребностях в пунктах назначения.
Раздел 1.
Линейное программирование.
Предметом изучения данного раздела являются линейные экстремальные задачи, в которых целевая функция и функция ограничения линейны.
Определение: общей задачей линейного программирования называется задача, состоящая в нахождении максимального значения целевой функции.
1) Z= 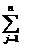 cjxj
cjxj 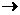 max при условии
max при условии
2) 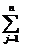 aijxj{
aijxj{ 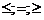 } bi(i=
} bi(i= 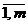 )
)
3) xj 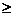 0 (j
0 (j 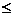 n)
n)
где aij; bi; cj – заданные постоянные величины,
1. целевая функция задачи (линейная форма)
2. ограничение задачи (типа равенства или неравенства)
3. условие неотрицательности переменной
Определение: стандартной (симметричной) задачей ЛП называется задача, в которой целевая функция исследуется на максимум или минимум, ограничение только типа неравенств, причем в одну сторону, а для всех переменных выполняется условие неотрицательности.
Определение канонической формы задач.
Канонической (основной) задачей линейного программирования называется задача, в которой:
1) функция цели исследуется на максимум или минимум 2) ограничение задачи только типа неравенства (в одну сторону)
3) все переменные неотрицательны (xj ≥ 0)
4) элементы столбца правых частей положительны (bi>0 i= 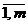 )
)
Определение: совокупность n-чисел (x1……xn), удовлетворяющих ограничению задачи, назовем допустимым решением или планом задачи. План X*=(X  …X
…X  ) называется оптимальным, если на нем целевая функция принимает максимальное (минимальное) значение.
) называется оптимальным, если на нем целевая функция принимает максимальное (минимальное) значение.
Элементы выпуклого анализа.
Линейная комбинация векторов (*) R=a1A1+…+anAn называется выпуклой, если выполняется условие:
 ai=1 и все ai неотрицательны.
ai=1 и все ai неотрицательны.
В двухмерном случае выпуклой комбинацией двух векторов (точек двухмерного пространства) есть отрезок, их соединяющий.
Определение: множество называется выпуклым, если вместе с каждой парой своих элементов, оно содержит все их выпуклые комбинации.
выпуклое невыпуклое
множество множество
Система линейных неравенств в ограничениях задачи ЛП стандартной формы определяет некоторое выпуклое возможно неограниченное множество, которое называют многогранником решений.
 | |||
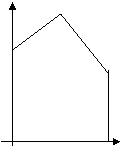 | |||
Ограниченный и Неограниченный
многогранники решения.
Определение: угловая точка многогранника решений – это такая точка многогранника, которая не является выпуклой линейной комбинацией никаких других точек многогранника (не лежит на отрезке, соединяющим две другие точки многогранника).
Если система ограничений содержит конечное число неравенств, то число угловых точек будет конечно и не превосходит С 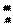 -числа сочетаний.
-числа сочетаний.
Теорема № 1.
Целевая функция задач линейного программирования достигает своего максимального значения в одной или нескольких угловых точках многогранника. Если она принимает максимальное значение большие, чем в одной из угловых точек, то она достигает такого же значения и в любой точке, являющаяся выпуклой линейной комбинацией этих угловых точек. Содержательно: это означает, что прямая, соответствующая целевой функции, параллельна одной из граней многогранника.
Опорное и базисное решение.
Если система линейных уравнений имеет переменных больше, чем уравнений, то она имеет бесконечное множество решений, в каждом из которых некоторые переменные полагают как базисные, а некоторые как свободные, причем базисных ровно столько, сколько уравнений в системе, а свободных n-m, где n – число переменных, а m – число уравнений. Применительно к задачам линейного программирования при переходе к канонической форме всегда имеем систему, в которой число неизвестных больше числа уравнений. При этом столбец B является линейной комбинацией (см. векторное представление задач) векторов A1+…+An и некоторых дополнительных, которые возникают в результате перехода к канонической форме. Следовательно, в качестве базисных переменных можно выбрать только m-переменных, а остальные все переменные в силу их не отрицательности положить равными нулю. Такое решение называется опорным.
Рассмотрим канонический вид задачи ЛП:
Z=C1X1+…+CnXn 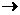 max
max
(*) A1X1+…+AnXn=B
Xj³0 j= 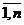 .
.
B>0
Симплексный метод.
Основная идея: Симплекс метод – это направленный перебор опорных решений задачи линейного программирования, при котором значения целевой функции на каждом следующем шаге больше (не меньше), чем на предыдущих.
По процедуре метода переход от одной угловой точки к другой осуществляется с помощью преобразований Жордана - Гаусса. Преобразования осуществляются над строками матрицы и состоят в следующем:
1)перемена строк местами
2)умножение строки на число, отличное от нуля
3)сложение двух строк покомпонентно (элементов, стоящих в одном столбце).
Для решения задач симплекс- методом следует выполнить действия:
0) Построить экономико - математическую модель задачи
1) Привести задачу к канонической форме.
2) Составить исходную симплекс таблицу
3) Проверить план на оптимальность.
4) Если план не оптимальный, то переходим к новому опорному плану с помощью преобразований Жордана-Гаусса.
Задача № 1.
Предприятие планирует выпуск трех видов изделий и при этом предполагает использовать три вида ресурсов. Известны цена реализации (прибыль) единицы каждого вида изделия C1,C2,C3, запасы ресурсов каждого вида В1, В2, В3, расходы каждого вида ресурсов на производство единицы каждого вида продукции aij. Требуется составить план производства ( указать сколько и какой продукции надо выпускать, чтобы получить максимальную прибыль от ее реализации).
a) Составление экономико-математической модели:
В качестве переменных Х1,Х2,Х3 выбираем количество продукции каждого вида. Следовательно, значение этих переменных неотрицательно.
b) Целевая функция выражает прибыль от реализации и, следовательно, имеет представление Z=C1X1+C2X2+C3X3 и исходя из содержания задачи она должна быть максимальной.
c) Ограничения:
· Не отрицательность переменных из пункта а)
· Ограничение по ресурсам. Расход каждого вида ресурса на производство всех видов продукции не превосходит их заданных объемов:
a1x1+…..+a1nxn≤b1
……………
am1x1+…..+amnxn≤bm
Из содержания задачи b1 и bm должны быть положительны, т.к. это запасы ресурсов.
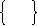 Дано: C1=5, C2=4, C3=3 , aij
Дано: C1=5, C2=4, C3=3 , aij
В1=50, В2=60, В3=30.
Целевая функция Z=5x1+4x2+3x3 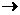 max выражает собой прибыль от реализации продуктов.
max выражает собой прибыль от реализации продуктов.
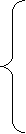 4x1+3x2+x3
4x1+3x2+x3 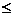 40
40
2x1+5x2+2x3 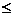 50
50
x1+2x2+4x3 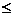 60
60
x1,x2,x3 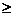 0
0
Для решения задачи симплекс-методом приводим ее к канонической форме. В данном случае не выполняется лишь одно условие канонической формы, а именно ограничения должны быть типа равенства. Для перехода к ограничениям типа равенства в левую часть каждого из неравенств вводится своя неотрицательная добавочная переменная (в случае если левая часть меньше или равна правой), и избыточная неотрицательная переменная вычитается (в случае если левая часть больше или равна правой), которые входят в функцию цели с нулевыми коэффициентами.
 Z=5x1+4x2+3x3+0x4+0x5+0x6
Z=5x1+4x2+3x3+0x4+0x5+0x6 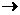 max
max
x1+3x2+2x3+x4 =40
4x1+x2+x3+x5 =50
2x1+2x2+x3 +x6=60
x1,x2,x3,x4,x5,x6 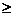 0
0
Это есть каноническая форма задачи. Для решения симплекс-методом составляется исходная симплекс-таблица.

Т.к. симплекс-метод есть направленный перебор угловых точек (опорных решений), то необходимо определить исходное опорное решение, отправляясь от которого с помощью процедур симплекс-метода определим хотя бы одно оптимальное или установим неразрешимость задачи.
Каждое опорное решение определяется некоторым базисом векторов-условий, и т.к. размерность векторов равна 3, то базис должен содержать ровно 3 вектора. Из канонической формы задачи определяем «явные» базисные вектора размерностью три А1, А2, А3, т.к. это три единичных вектора размерностью три, которые образуют базис. Следовательно, все остальные переменные Х1,Х2,Х3должны быть равны нулю.Из уравнения канонической формы видно, что Х4=50, Х5=60, Х3=30.
Таким образом, получим исходный опорный план Х0=(0,0,0,50,60,30), значение целевой функции на котором равно нулю, что соответствует естественной постановке задачи, а именно если ничего не производится Х1,Х2,Х3=0, то и прибыль отсутствует. В столбец B заносим коэффициенты целевой функции при базисных переменных. В столбец В заносим значения базисных переменных.
m+1 строка называется строкой оценок или индексной (Zj – Cj)
Zj – значение функции цели на j-векторе и равно скалярному произведению двух векторов СБ и Аj: Zj=СБ*Aj
На пересечениях индексной строки и столбца В находятся значения целевой функции на данном опорном плане.
План оптимальный в задаче на максимум (минимум), если все оценки индексной строки не отрицательные (не положительные).
Следствие:
Если среди оценок индексной строки есть отрицательные, то данный план неоптимальный и его можно попытаться улучшить с помощью преобразований Жордана-Гаусса (согласно следующей теореме).
Теорема 4.2 «О переходе к новому опорному плану»
Для перехода к новому опорному плану (к новому базису отличного от данного) будем следовать следующим правилам:
1. Правило определения вектора вводимого в базис.
Расширенная задача.
Пусть требуется найти min Z=C1X1+…+CnXn при ограничениях:
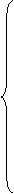 a11x1+…+a1nxn=b1
a11x1+…+a1nxn=b1 
………………… (*)
am1x1+…+amnxn=bm
xj 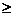 0 j=
0 j= 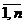
bj>0 i= 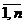
Определение: Задача, состоящая в нахождении минимума функции
 F=C1X1+…+CnXn+MXn+1+…+MXn+m min , при ограничениях
F=C1X1+…+CnXn+MXn+1+…+MXn+m min , при ограничениях
xj 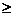 0 j=
0 j= 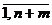
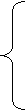 a11+…+a1nxn+xn+1 =b1
a11+…+a1nxn+xn+1 =b1
…………………………
am1x1+amnxn+…+xn+m=bm
где М - некоторое достаточно большое положительное число, конкретное значения которого обычно не задается, называется расширенной задачей по отношению к задаче (*).
Содержательно: Если в канонической форме задачи нет вообще единичного базиса (или он частичный), то в левой части ограничений вводится столько искусственных переменных, сколько не хватает векторов до единичного базиса, которые входят в функцию цели с коэффициентом М, конкретное значение которого может быть не задано заранее (или же его значение на 3-4 порядка больше, чем порядок коэффициента целевой функции).
В этом случае всегда существует опорное исходное решение расширенной задачи X0=( 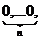 b1…bn), которое определяется системой из n искусственных единичных векторов.
b1…bn), которое определяется системой из n искусственных единичных векторов.
Теорема 5.1
Если в оптимальном плане X*=( X 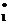 … ,X
… ,X 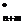 ) расширенной задачи значения всех искусственных переменных равны нулю, то план
) расширенной задачи значения всех искусственных переменных равны нулю, то план 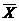 *=(
*=( 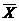
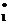 , …, X
, …, X  ) исходной задачи является оптимальным планом исходной задачи.
) исходной задачи является оптимальным планом исходной задачи.
Содержательно: если в найденном оптимальном плане расширенной задачи все искусственные переменные равны нулю, то имеем оптимальный план исходной задачи.
Замечание: возможна ситуация, когда в плане расширенной задачи все искусственные переменные равны нулю, но при этом он не будет оптимальным планом исходной задачи, и поэтому его следует довести до оптимального плана исходной задачи без искусственных переменных.
Исходная симплекс-таблица расширенной задачи.
Пусть X0=(0,…0, b1…bm) исходный опорный план расширенной задачи, тогда значение целевой функции f на данном плане равняется: F(X0)=М 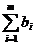 , а значения оценок будут равны: Zj-Cj=-M
, а значения оценок будут равны: Zj-Cj=-M 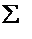 aij-Cj , следовательно значение целевой функции и значения оценок состоит из двух частей, одна из которых содержит M, а другая нет.
aij-Cj , следовательно значение целевой функции и значения оценок состоит из двух частей, одна из которых содержит M, а другая нет.
Тогда в отличии от классического симплекс-метода таблица содержит две индексные строки (m+1) и (m+2). В (m+2) строку заносят коэффициент при М, а в (m+1) - часть оценки, не содержащую М.
Вычисления (пересчет симплекс-таблиц) проводятся по (m+2) строке до тех пор пока:
1. Либо все искусственные вектора не будут исключены из базиса.
2. Либо не все искусственные вектора будут исключены, но (m+2) строка не содержит больше положительных элементов, соответствующих искусственным векторам.
В первом случае базис соответствует некоторому опорному плану исходной задачи, и определение ее оптимального плана проводим только по (m+1)строке.
Во втором случае, если элемент, стоящий на пересечении (m+1) строк и столбца B отрицателен, то исходная задача не имеет решения (признак неразрешимости), а если же он равен нулю, то найденный опорный план исходной задачи является вырожденным (для данного метода), и базис содержит, по крайней мере, хотя бы один из искусственных векторов.
Если исходная задача содержит несколько единичных векторов (<m), то их следует вводить в искусственный базис; искусственных переменных столько, сколько не хватает векторов до единичного базиса.
Экономическая интерпретация
Прямая: сколько и какой продукции необходимо произвести, чтобы при заданных ценах реализации, объемах и заданном способе производства получить максимальную прибыль от реализации произведенной продукции. Z=CX 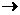 max AX£B X³0 max AX£B X³0 | Двойственная: какова должна быть оценка цены единицы каждого вида ресурсов, чтобы при имеющихся их объемах, величин стоимости реализации и заданном способе производства, минимизировать общую оценку стоимости затрат. F=BY 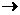 min ATY³C Y³0 min ATY³C Y³0 |
Лемма 1.
Для любых планов X и Y прямой и двойственной задач соответственно (прямая – максимум, двойственная – минимум) имеет место Z(X*) 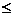 F(Y*), где Z – целевая функция переменной, F – функция двойственной задачи.
F(Y*), где Z – целевая функция переменной, F – функция двойственной задачи.
Теорема 6.3.
Пусть X*=(X 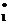 ,…X
,…X  ) допустимое решение прямой задачи. Вектор X* является оптимальным решением прямой задачи тогда и только тогда, когда среди решений системы уравнений (1) при X
) допустимое решение прямой задачи. Вектор X* является оптимальным решением прямой задачи тогда и только тогда, когда среди решений системы уравнений (1) при X 
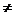 0 содержалось хотя бы одно допустимое решение двойственной задачи, в которой yi=0 при
0 содержалось хотя бы одно допустимое решение двойственной задачи, в которой yi=0 при 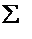 aijxj<bi.
aijxj<bi.
Теорема 8.1
В оптимальном плане двойственной задачи Y* значение переменной y*i численно равно частной производной оптимального значения целевой функции (производная значения целевой функции берется как от функции объема ресурсов) Zmax (b1…bm) по данному аргументу.
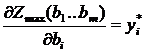
Изменение объемов дефицитных ресурсов приводит к изменению значений целевой функции на оптимальном плане. И это изменение определяется величиной y*i и характеризуется лишь в случае, когда данное значение положительно. Эта характеристика скорости изменения (интенсивности) оптимального значения целевой функции в зависимости от интенсивности изменения объемов ресурсов. При расширении производства требуется определить выбор тех видов ресурсов, увеличение объемов которых позволит наиболее эффективно организовать производство данного вида продукции. Для данной задачи расширение возможно только второго вида.
Раздел II.
Специальные задачи ЛП
Пример: «Задача о рюкзаке (задача загрузки корабля)»
Имеется n видов предметов, j-й предмет имеет массу aj и ценность cj. Следует загрузить рюкзак вместимостью В, так что ценность груза была максимальной.
Xj- -количество предметов j-ого вида (неделимых)
Тогда 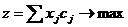 при ограничениях:
при ограничениях:
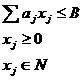
Пример: «Задача о распределение инвестиций»
 Имеется n проектов и для любого j-ого проекта определен эффект от реализации γj при необходимых объемах инвестиций gj, т.е. γj gj.
Имеется n проектов и для любого j-ого проекта определен эффект от реализации γj при необходимых объемах инвестиций gj, т.е. γj gj.
Общий объем инвестиций не превышает В. Определить, какие проекты нужно реализовать, чтобы суммарный эффект был максимальным.
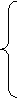 Х= 0 если Рj не реализуется
Х= 0 если Рj не реализуется
1 если Рj реализуется
Тогда 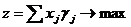 при ограничениях
при ограничениях 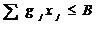
Схема алгоритма
1. Пусть в результате решения ослабленной задачи получен оптимальный план, имеющий хотя бы одну нецелочисленную компоненту.
Замечание: 1-й алгоритм Гомори решает только полностью целочисленные задачи, поэтому результатом его решения может быть оптимальный план только с целочисленными компонентами.
2. В симплекс-таблице оптимального решения выбираем значение базисной переменной задачи Х*j с наибольшей дробной частью. Если таких переменных несколько, то выбираем любую.
Этой переменной соответствует строка симплекс-таблицы, называемая строкой, производящей отсечение (производящей строкой).
Выписывается уравнение
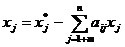 (полагая, что первые m переменных базисные для данного оптимального решения).
(полагая, что первые m переменных базисные для данного оптимального решения).
На основании этой строки, предполагаем, что m первые переменные являются базисными, и т.к. коэффициенты целевой функции - целые числа, то значение целевой функции на целочисленном решении также должно быть целочисленно.
Представим каждый коэффициент данной строки в виде целой и дробной частей.
Тогда 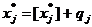 0<qj<1
0<qj<1

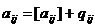 0≤qj<1
0≤qj<1
qj - положительная дробь
qij - неотрицательная дробь
Переносим все целые части коэффициентов в одну сторону, оставляя все дробные в другой:
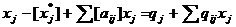
Так как все переменные xm+1,...,xn принимают целочисленные значения и силу их небазисности, то правая часть уравнения является целочисленной. Следовательно, в силу неотрицательности дробных частей и переменных задачи и левая часть должна быть неотрицательна:
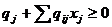 , следовательно,
, следовательно, 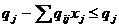
Так как qj<1, заменяя в правой части qj, получим строгое неравенство 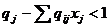
Так как левая часть неравенства должна принимать целые значения, то, следовательно, необходимое условие ее целочисленности можно записать только в следующем виде: 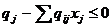
Вводя остаточную переменную Sj (переменную Гомори), получим 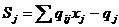
Где Sj – неотрицательная добавочная переменная, которая по определению должна принимать целочисленное значение, что для данной системы ограничений при xj=0 имеет вид: 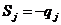
Следовательно, она принимает отрицательное значение, т.е. является недопустимой, и, таким образом, полученное ранее решение ослабленной задачи не удовлетворяет данному ограничению. В этой ситуации обычно используют двойственный симплекс-метод или М-метод.
Вывод: строится ограничение, которому не удовлетворяет оптимальный нецелочисленный план. Следовательно, надо решить задачу с исходной целевой функцией и расширенной системой ограничений.
Метод ветвей и границ.
Идея метода: пусть решена задача без условия целочисленности и х*r – целочисленная переменная, значение которой в оптимальном плане является дробным. Тогда интервал [х*r]< х r<[х*r]+1 не содержит допустимых решений с целочисленной координатой хr. Следовательно, допустимое решение с целочисленной координатой хr удовлетворяет одному из следующих условий : [ х r≤[х*r] или х r≥[х*r]+1.
Введение этих условий в исходную задачу порождает две несвязанных между собой задачи с одной и той же целевой функцией, но не пересекающихся областями допустимых решений. В этом случае говорят, что задача разветвляется.
Осуществляемый в процессе учет необходимых условий целочисленности позволяет исключить часть многогранника решений, не содержащих решений с целочисленной координатой х r.
Геометрическая интерпретация:
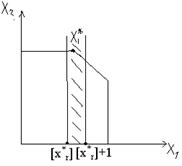 Вырезаем «полосу», не содержащую решение с целочисленной координатой х1. Затем решаем каждую из подзадач. Если полученный оптимум окажется допустимым для целочисленной задачи, то значение его фиксируется как наилучшее, и при этом нет необходимости продолжать ветвление данной подзадачи. В противном случае подзадача, в свою очередь, разбивается на две подзадачи при условие целочисленности значений, которые в оптимальном плане не оказались целыми. Как только полученное допустимое целочисленное решение одной из подзадач окажется лучше имеющегося, то одно фиксируется вместо зафиксированного ранее.
Вырезаем «полосу», не содержащую решение с целочисленной координатой х1. Затем решаем каждую из подзадач. Если полученный оптимум окажется допустимым для целочисленной задачи, то значение его фиксируется как наилучшее, и при этом нет необходимости продолжать ветвление данной подзадачи. В противном случае подзадача, в свою очередь, разбивается на две подзадачи при условие целочисленности значений, которые в оптимальном плане не оказались целыми. Как только полученное допустимое целочисленное решение одной из подзадач окажется лучше имеющегося, то одно фиксируется вместо зафиксированного ранее.
Процесс ветвления продолжается до тех пор, пока не приведет к целочисленному решению или пока не будет установлена невозможность сосуществования такого, либо улучшение уже имеющегося.
Эффективность вычислительной схемы существенно повышается с введением понятия «граница», на основе которого делается вывод о необходимости дальнейшего разбиения каждой из подзадач.
Суть: если оптимальное решение подзадачи без условия целочисленности обеспечивает худшее значение целевой функции, чем имеющееся ранее, то подзадача далее не рассматривается, и говорят, что она прозондированна, и ее можно вычеркнуть из списка подзадач, порожденных исходной задачей. Другими словами, как только получено допустимое целочисленное решение, соответствующее значение целевой функции может быть использовано в качестве верхней (в случае минимизации) или нижней (в случае максимизации) границы, наличие которой позволяет формализовать процедуру исключения прозондированных задач. Этот метод позволяет решать как полностью, так и частично целочисленные задачи.
Транспортная задача
1. Транспортная задача. Распределительный метод.
2. Метод потенциалов (Канторовича)
3. Задача о назначениях. Венгерский алгоритм.
Классическая транспортная задача – это задача о наиболее экономичном плане перевозок однородного (или взаимозаменяемых) продукта из заданных пунктов отправления (пункта производства или хранения) в пункты назначения (пункты потребления данного продукта). Наиболее часто встречается в распределительных экономических задачах.
Эта задача связана с территорией, распределением, назначениями, транспортом и размерами производства. Кроме того, различные варианты этой задачи встречаются в задачах организации производства, принятия решений и организационного управления.
Классическая подстановка: имеется m пунктов производства или складирования однородного продукта, запасы которого равны соответственно A1…Ai….Am. Имеется n пунктов потребления этого же продукта с потребностями В1…Вj….Вn. Известны тарифы (транспортные расходы, связанные с доставкой единицы продукта из заданного пункта отправления в заданный пункт потребления)
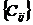
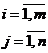
Требуется составить план перевозок (указать какое количество из какого пункта отправления и в какой пункт потребления следует перевезти продукт), обеспечивающий наиболее экономичным путем (при суммарных минимальных затратах на перевозку) удовлетворение всех пунктов потребления за счет реализации всего продукта, находящегося в пунктах отправления.
Фактически требуется указать вектор 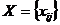 поставок (
поставок ( 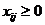 ), где xij – количество единиц продукта, направленного из i-го пункта отправления в j-й пункт потребления и удовлетворяющий следующим условиям:
), где xij – количество единиц продукта, направленного из i-го пункта отправления в j-й пункт потребления и удовлетворяющий следующим условиям:
1) Условие полного удовлетворения потребностей всех пунктов потребления.
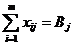
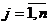
2) Весь продукт, хранимый на базах, должен быть вывезен.
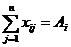
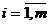
и дающий минимум целевой функции
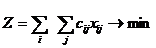
Транспортная задача исследуется только на минимум.
Определение: Транспортная задача называется закрытой (сбалансированной), если суммарный объем запасов равен суммарному объему потребностей:
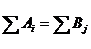
В противном случае она называется открытой.
Теорема 1 (необходимое условие разрешимости транспортной задачи)
Транспортная задача разрешима тогда и только тогда, когда она сбалансированная.
Если задача открытая, то ее всегда можно привести к закрытой, при этом следует произвести следующие преобразования:
а) Случай дефицита (суммарное потребление строго больше суммарных запасов). В этом случае вводят фиктивный пункт отправления с запасами, равными 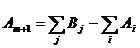 , из которого перевозка во все пункты назначения осуществляется по нулевым тарифам.
, из которого перевозка во все пункты назначения осуществляется по нулевым тарифам.
б) Случай избытка продукта. Вводится фиктивный пункт потребления с потребностями 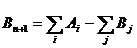 , перевозки в который со всех пунктов отправления осуществляются по нулевым тарифам.
, перевозки в который со всех пунктов отправления осуществляются по нулевым тарифам.
Вторая транспортная теорема
Х – невырожденный опорный план, который не является оптимальным, т.е. среди свободных клеток есть положительные. Тогда:
1) среди положительных оценок свободных клеток выбираем наибольшее, и для этой клетки строим цикл, в котором выставляем чередующие знаки – и +, начиная со свободной клетки.
2) среди всех поставок положительных клеток цикла выбирается наименьшая, которая затем прибавляется к поставкам в отрицательных клетках цикла и вычитается из поставок положительных клеток цикла. В результате такого преобразования получаем новый опорный план, который может быть вырожденным (это возможно если наименьшая «положительная» поставка находится в двух или более клетках цикла). И тогда прежде чем проверять полученный план на оптимальность, его следует сделать не вырожденным.
Замечание: если клеток с наибольшей положительной оценкой несколько, то для каждой из них следует построить цикл, расставить знаки и определить величину минимальной положительной поставки. Выбираем клетку для перераспределения, для которой найденная положительная поставка цикла будет наибольшей, и именно по данному циклу осуществляем переход к новому опорному плану.
Математические методы теории оптимизации.
Понятие экстремальных задач, примеры. Основные понятия ЛП.
В связи с расширением круга приложений математики к различным направлениям экономики в последнее время применение классических методов оказалось затруднительным в силу возросшей сложности и разнообразия возникших проблем. В первую очередь это относится к задачам управления, различным задачам выбора, разрешения конфликтных ситуаций, задачам обслуживания и т.п.
Такого рода задачи решение достигается, как правило, в граничных точках области изменения исследуемых параметров. В этой связи классических методов недостаточно и исследование экономических задач привело к возникновению нового направления, предметом изучения которого является: формализация, постановка, нахождение методов решения различных классов задач, связанных с теми или иными проблемами оптимизации, и анализ полученных результатов с целью их практического использования. Всякая оптимизация связана с наличием ограничений: на ресурсы, на способы действий, на возможности. В экономических задачах управления и планирования процесс решения обычно сводится к выбору системы функции и системы параметров, которые называются характеристиками экономической системы. В настоящее время главным образом под характеристиками понимают только систему параметров. Таким образом, проблема управления и планирования сводится к экстремальным задачам следующего вида:
(1) требуется определить max (min) f(xi..xn), при условии:
(*) gi(xi…xn) {£;=;³}bi
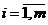
(**) xj³0 j£n, где
– f(xi…xn) – показатель качества решений (целевая функция) и.
– условия (*) и (**) – ограничения, которые определяют некоторое множество допустимых решений (область определения целевой функции).
Для того, чтобы решить экстремальную задачу (1), достаточно найти ее оптимальное значение (указать значение всех переменных, удовлетворяющих ограничениям задачи, которые доставляют функции f наибольшее или наименьшее значение среди всех значений функции на допустимых множестве переменных или доказать, что таких решений нет).
Процедура нахождения решения экстремальных задач называется процедурой оптимизации.
1. Задача (1) является неразрешимой, если она не имеет решения. Это возможно в случае, когда целевая функция не ограничена на допустимом множестве решений. Решить экстремальную задачу – найти ее оптимальное решение, либо установить ее неразрешимость.
2. Математическая дисциплина, занимающаяся изучением экстремальных задач и разработкой методов их решений при различных допущениях относительно для различных функций fi и gi, называется математическим программированием, или математическими методами оптимизации.
Основная особенность экстремальных задач, в отличие от задач на условный экстремум, состоит в наличии неравенств среди ограничений и, следовательно, классические методы не применимы.
Методы решения задачи (1) во многом зависят от тех или иных свойств множества допустимых значений, и поэтому методы оптимизации рассматриваются как совокупность ряда самостоятельных дисциплин. Все задачи можно условно разделить на два больших класса: линейные и нелинейные.
Для задач первого класса характерна линейность целевой функции и функций, входящих в ограничение. Для этого класса задач существует универсальный метод их решения. Среди задач нелинейного программирования разработаны алгоритмы решения только для задач выпуклого программирования.
Отдельным классом задач являются задачи целочисленного и динамического программирования. И в последнее время особое внимание уделяется методам теории игр для анализа рыночных отношений и сетевого планирования моделирующего процесса реализации проектов во времени, а также задач распределения ресурсов и продуктов.
Историческая справка.
В 1930 году А.Н. Толстым в сборнике «Планирование перевозок» была изложена методика составления плана перевозок, обеспечивающего наименьший суммарный пробег. По существу, была сформулирована впервые транспортная задача, но при этом не приводилось точных математических формулировок и формальных доказательств. Первая строгая математическая постановка была предложена в 1941 году Ф. Хичкоком, в честь которого эта задача в западной литературе именуется проблемой Хичкока.
В 1931 году венгр Эгервари рассмотрел и решил задачу выбора «Венгерским алгоритмом».
В 1939 году Л.В. Канторович в книге «Математические методы организации и планирования производства» предложил решение задачи по распределению обработки пяти видов материалов между восьмью станками.
Во время второй мировой войны ряд американских ученых и английских математиков был привлечен
