Методика ознакомления детей с цифрами

МАТЕРИАЛЫ

ДЛЯ САМОСТОЯТЕЛЬНОЙ ПОДГОТОВКИ СТУДЕНТОВ

К КУРСОВОМУ ЭКЗАМЕНУ ПО ДИСЦИПЛИНЕ

«ТЕОРИЯ И МЕТОДИКА МАТЕМАТИЧЕСКОГО РАЗВИТИЯ ДЕТЕЙ ДОШКОЛЬНОГО ВОЗРАСТА»

Отделение

«Дошкольное образование»

ГРУППЫ 141, 151

Преподаватель Семёнова Е.В.

2012 – 2013

ЗАДАНИЯ НА ЭКЗАМЕНЕ:

· Ответы на вопросы экзаменационного билета: теоретический и методический

· Защита проекта непосредственной образовательной деятельности (организованного обучения) в форме игры-занятия, игровой проблемной ситуации: представить оформленный в соответствии с требованиями конспект для группы практики, демонстрационный материал и образец раздаточного материала

· Презентация портфолио достижений: печатные теоретические материалы по содержанию курса; практические материалы, подобранные самостоятельно; перечень изготовленных наглядных дидактических материалов (желательно предъявление фотографий)

ТЕМЫ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ

1. Второе направление работы по теме «Формирование представлений о числах» – образование чисел, натуральный ряд …………………………………3

2. Методика ознакомления детей с цифрами…………………………………..…..4

2 А. Обучение счёту в пределах двадцати (дополнительный материал)…….….5

3. Цветные цифры Х.Кюизенера……………………………………………………7

4. Деление целого на равные части………………………………………...……….9

5. Методика ознакомления детей с арифметическими задачами……………….10

6. Развитие геометрических представлений в дошкольном возрасте……..……15

7. Обучение детей ориентировке в пространстве……………………………...…33

8. Развитие представлений о времени у детей дошкольного возраста………….40

8 А. Развитие у дошкольников чувства времени (дополнительный материал)..45

ВТОРОЕ НАПРАВЛЕНИЕ РАБОТЫ ПО ТЕМЕ «ФОРМИРОВАНИЕ ПРЕДСТАВЛЕНИЙ О ЧИСЛАХ» – ОБРАЗОВАНИЕ ЧИСЕЛ, НАТУРАЛЬНЫЙ РЯД

В процессе освоения механизма счёта дети делают первые шаги в освоении принципа образования числа и натурального ряда. Специально эту работу проводят в старшем возрасте.

1 упражнение

{{{{{{{ï{ Сколько цветов? Как получили 8 цветов?

OOOOOOO Если к 7 флажкам добавить ещё один, сколько станет? А если убрать?

rrrrrrr Что надо сделать, чтобы получилось 8 кубиков?

Обобщение: как получилось число 8? Ту же работу выполняем в обратном направлении: как из числа 8 получить число 7.

2 упражнение

Построение числовой лесенки. Вопросы: Как получили число 5? Какое число больше, 6 или 5? Какое число меньше, 5 или 6? Как узнали? На сколько 5 меньше, чем 6? Как получить из числа 5 число 6?Из 6 пять? Какое число получится, если к 5 добавить 1, из 5 убрать 1? Какое число больше, чем 5 на 1?

Таким образом рассмотреть ВСЕ свойства рядом стоящих чисел. Числовая лесенка позволяет соотнести цифру и количество. На основе этой модели дети получают первые представления о натуральной последовательности.

3 упражнение

На основе знаний цифр дети вместе с воспитателем составляют натуральный ряд через постепенное (по одному) появление предметов и их обозначение цифрами:

¶¶¶ … ð 1 2 3 …

Дети учатся различать понятия до, после, предыдущее, последующее число: открыли одну звездочку, сколько звёздочек? Какую цифру надо положить? Сколько будет звёздочек, если я открою еще одну? Какое следующее число вы назовете? Какую цифру надо положить? 1 стоит перед числом 2, 2 – после числа 1. 1 – предыдущее число, 2 – последующее число.

4 упражнение «Лягушонок»

Найти число 6. Посадить лягушонка на предыдущее число. Найти число, больше чем 6 на 1. Найти число, стоящее перед числом 5, после числа 6 и т.д.

5 упражнение «Сказочные цифры» (Истомина Н.Б., стр. 24, «Математика на 5», стр. 31-34).

- Один гномик нашёл столько грибов, а другой – столько. Кто нашел больше?

- Гномик нашел столькогрибов, друг подарил ему ещё 1. Покажите, сколько стало грибов у первого гномика.

- Красная Шапочка принесла бабушке столько пирожков. Бабушка съела один. Покажите, сколько осталось пирожков.

- Какое число больше: это или это? Как догадались? На сколько?

6 упражнение

Знакомство с числовым лучом. Передвижения по числовому лучу. Упражнения «Назови соседей», «Называй дальше».

7 упражнение

1 2 3 4 5 6 7 8 9

Выбрать ряд чисел, которым можно пользоваться при счёте. Что пропущено? Разложи по порядку («Путаница»). Найди ошибку. Продолжи ряд. Разгадай закономерность. «Цифровая цепочка»

НАЗЫВАНИЕ ЧИСЕЛ В ОБРАТНОМ ПОРЯДКЕ.

Процесс счёта носит векторный характер в сторону увеличения числа. Число, названное при счёте последним, есть ответ на вопрос сколько? Обучение ведется на наглядном материале: предметы убирать по одному, справа налево, при этом называется оставшееся количество предметов.

Называть числа в обратном порядке с опорой на числовой луч.

Как почтальону быстрее отнести письмо в дом № 6?

Это – девятая чашка. Покажи пятую.

«Назови соседей», «Назови предыдущее число», «Кто знает, пусть дальше считает», «Разложи картинки по порядку», «Назови меньшее на 1».

В результате проведенной работы ребёнок должен уметь ответить на вопросы, отражающие связи и отношения между числами, а также рассказать о числах, например, 7 и 6: 7 больше 6 на 1, 6 меньше 7 на 1; чтобы получить 7, надо к 6 добавить 1; чтобы получить 6, надо из 7 убрать 1; число 6 стоит перед числом 7, число 7 стоит после числа 6.

ЦВЕТНЫЕ ЦИФРЫ Х.КЮИЗЕНЕРА

Для углубления представлений о числе, о связях и отношениях между числами натурального ряда широко используются цветные палочки (цифры) бельгийского математика Х.Кюизенера.

Принцип: понятие итогового числа формируется путём измерения числа с помощью общей условной меры.

Значение «цветных цифр»: осознание отношений больше, меньше, равно, больше на, меньше на; относительность свойств, транзитивность отношений; деление целого на части; измерение с помощью условной меры; осознание функциональной зависимости; состав чисел из единиц и двух меньших; смысл арифметических действий; пространственная ориентировка: справа, слева; логические отношения: такой же, не такой; сериация.

Цвета, в которые окрашены палочки-цифры, выбраны не произвольно: они зависят от отношений, определяемых простыми числами первого десятка. Числа, кратные двум, имеют оттенки красного цвета, кратные трем – синего, пяти – желтого.

число	цвет палочки	обозначение
	белый	Б
	розовый	Р
	голубой	Г
	красный (2х2)	К
	желтый	Ж
	фиолетовый (2х3)	Ф
	чёрный	Ч
	вишневый (2х4)	В
	синий (3х3)	С
	оранжевый (2х5)	О

Методика работы.

· Сначала дети составляют изображения из палочек на листе нелинованной бумаги, т.е. знакомятся с пособием в игровой, практической, творческой деятельности: называют цвета, подбирают по длине в зависимости от детали изображения. Сравнивают по длине, группируют.

· Дети составляют изображения (животные, заборчики, коврики) на листе клетчатой бумаги, причем размер клетки должен быть равен стороне белого квадрата. Строят сериационные ряды. В процессе этой работы дети обращают внимание на то, сколько клеточек занимает каждая палочка.

· Специальная работа по знакомству с тем, какое число каждая палочка обозначает.

1) Возьмите одну розовую палочку.

2) Сколько клеток она занимает?

3) Сколько нужно взять белых кубиков, чтобы они поместились под розовой палочкой (вместе по длине были равны розовой палочке)?

4) Белый кубик – это число 1. Розовая палочка – число 2. Два – это один и один.

5) Положите столько грибов, какое число обозначает розовая палочка.

6) Добавьте еще один белый кубик.

7) Сколько стало белых кубиков? Найдите палочку, равную трем белым кубикам по длине. Какое число она обозначает? Как догадались? И т.д.

Анализ: как получилось число 2? 3? 4?... на сколько число 4 больше трех? Три меньше четырех? На сколько голубая полоска длиннее розовой? Сколько нужно взять белых палочек, чтобы получилось полоска, равная по длине желтой?

· Дети выстраивают сериационный ряд из палочек на листе клетчатой бумаги, палочки обозначаются цифрами. Проводится работа по сравнению рядом стоящих чисел, рассматриваются все их свойства по аналогии с числовой лесенкой.

· Порядковый счет: какая по цвету палочка лежит пятой по счету? Какого цвета палочка лежит между 5-ой и 7-ой? Какая по счету желтая полоска? Какая по счету полоска лежит между черной и синей?

· Дети составляют ряды наглядных пособий, выражающих равночисленные множества для обобщению по признаку числа: отсчитайте столько треугольников, сколько звуков услышали; найдите карточку, не которой столько же точек (числовую фигуру); найдите палочку; найдите цифру.

· Изучение состава числа из 2-х меньших.

Б	Ф
Р	Ж
Г	К
К	Г
Ж	Р
Ф	Б

· Игра с игральной костью: у каждого ребенка карточка 6х6. Дети бросают кубик, заполняют цветными полосками свободные поля. Выигрывает тот, кто первый заполнит свою карточку и объяснит состав числа 6.

I этап.

Практическое деление детьми множеств и предметов в повседневной деятельности, накопление эмпирического опыта. Дети овладевают понятиями части, делить, половина и др. Используются ролевые игры, чтение литературных произведений, например, «Два жадных медвежонка», «Мы делили апельсин», «Яблоко» Сутеева.

II этап.

Деление геометрических фигур на равные части путем складывания. Уточнить правила: совмещение углов, сторон. Сначала формируем представление о половине. Затем делим фигуры на 4, 8 частей разными способами.

Вопросы и задания: Что сделали? Сколько получилось частей? Покажи каждую. Как они называются? (половины, одна из четырёх, одна четвертая). Какой формы части? Равны ли части по величине? Как проверить? Покажите целое. Что больше, половина или целое? Сколько раз сложили, чтобы получилось 4 части? Сколько четвертых частей в целом? Одинаковы ли по величине половина большого круга и половина маленького круга? Почему?

Дети наблюдают за формой частей, их величиной, количеством сгибов. На наглядной основе сравнивают дробные числа:

III этап.

По линии сгиба г.ф. разрезаются, анализируются части и целое, затем путём наклеивания («жесткого восстановления») вновь целое составляется из частей.

Далее деление геометрических фигур осуществляется без наклеивания, после анализа полученных частей из них можно делать изображения (аппликация).

Полезно предлагать задания типа: Какую фигуру я разделила, если это одна из двух? Сколько раз надо сложить квадрат, чтобы получилось 4 части? Какой формы они могут быть? Если я попрошу дать одну четвертую квадрата, на сколько частей вы его разделите? Сколько четвёртых частей в прямоугольнике?

I V этап.

На этом этапе отрабатываются умения делить на части любые предметы и величины. Упражнения:

· разделить сок между тремя детьми поровну (мерка);

· разделить бревно пополам;

· нарисовать г.ф., линией разделить на 2 (4,6,8) частей; заштриховать одну вторую, три восьмых и т.д.

· разделить отрезок на 2(4) части разными способами;

· игра «Дроби» (Б.П.Никитин);

· игра «Равные доли»: ребёнок наугад вытаскивает несколько бобов из мешочка, делит на 2 равные части (это 2 очка), затем на 4 части (4 очка), на три части (3 очка). Выигрывает тот, кто больше наберет очков;

· «Дробная стенка»: сравнение долей (часть целого) и дробей (способ записи доли или нескольких долей)

1/2	1/2
1/3	1/3	1/3
1/4	1/4	¼	1/4
1/5	1/5	1/5	1/5	1/5
1/6	1/6	1/6	1/6	1/6	1/6

IV. По наличию сюжета.

1) Сюжетные текстовые.

2) Отвлеченные текстовые: «Я задумала число. Если к нему прибавить один, то получится 9. Какое число я задумала?».

Особенности восприятия детьми задач:

Решение простой задачи требует от ребёнка анализа её содержания, выделения данных и искомого, установления связей между ними, выбора арифметического действия. Без специального обучения дети не могут выполнить этот анализ.

Основные ошибки: решение задачи сводят к пересчитыванию предметов; при выборе арифметического действия опираются на смысловые глаголы; дав ответ, дети не могут объяснить решения; при составлении задач формулируют ответ вместе с условием, так как не видят значения вопроса: «На столе лежало 5 яблок. Одно яблоко взяли. Осталось 4 яблока»; не понимают значение некоторых слов, обозначающих действия: истратил, поделился, подарил; путают слова противоположного значения: дал – дали, взял – взяли и др.; формулируя вопрос, пользуются стереотипом: «Сколько стало?».

Этому способствуют типовые формулировки задач, предлагаемых воспитателем. В арифметических задачах (их называют нетиповыми) требование не всегда выражено вопросительным предложением: «В гараже стояло 2 легковых и 5 грузовых машин. Найдите количество машин в гараже». Текст задачи может быть выражен одним предложением, в котором дети затрудняются выделить условие и вопрос: «Сколько карандашей было у Маши, если 3 карандаша она отдала брату, а 4 оставила себе?».

СИСТЕМА РАБОТЫ ПО ОЗНАКОМЛЕНИЮ С АРИФМЕТИЧЕСКИМИ ЗАДАЧАМИ

БЕЛОШИСТАЯ А. Д/В № 8-9, 2005 ГОД.

В ДОШКОЛЬНОМ ВОЗРАСТЕ

С ГЕОМЕТРИЧЕСКИМИ ФИГУРАМИ

Направления работы:

· Знакомство с моделями геометрических фигур, их называние, узнавание, обследование, выделение в рисунках, чертежах

· Сравнение форм предметов с геом. фигурами как эталонами предметной формы

· Выделение элементов и свойств геометрических фигур, сравнение по этим свойствам

· Выполнение упражнений на геометрические преобразования: деление фигур, составление фигур, определение взаимного расположения фигур, их объединение, пересечение

· Решение логических задач геометрического характера

Первые сведения дети получают в играх с геометрической мозаикой, строительным материалом. Воспитатель употребляет правильные названия, идет накопление представлений.

Обследование геометрических фигур заключается в активном использовании зрительного, тактильного, двигательного анализаторов и в соединении полученных от них ощущений со словом.

Основные приемы работы

(ознакомление с кругом, квадратом, треугольником)

1. Предъявление геометрической фигуры с называнием.

2. Многократное обведение контура геом. фигуры пальцем в сопровождении слова, это обведение завершается скользящим движением ладони по всей поверхности фигуры.

3. Сравнение геом. фигур с выделением признаков сходств и различий по цвету, размеру, наличию углов, сторон, вершин, их количеству, соотношению, направлению линий.

4. «Вырисовывание» контура геом. фигуры в воздухе, на столе и т.п..

5. «Пробовательные» действия для выявления свойств геом. фигур (прокатить, просунуть).

6. Наложение, приложение.

7. Игры.

I ЭТАП – 3-4 года.

Цель: познакомить с понятием «круг», учить называть и различать круги по цвету и величине.

Знакомство с геом. фигурами начинается с предъявления двух кругов разного цвета и размера. - Что это? - Какого они цвета? Величины? Чем отличаются? Чем похожи?

Далее обвести пальцем по контуру, прорисовать, прокатить, наложить друг на друга и выполнить упражнения на закрепление (сложить картинку «Неваляшка», выложить «бусики» и т.п.).

II ЭТАП – 3-4 года.

Цель: дать представление о квадрате, научить различать и называть круг и квадрат, упражнять в обследовании этих геом. фигур.

Сюрпризное внесение круга и квадрата (одного цвета, подобранных таким образом, чтобы круг вписывался в квадрат). Сначала рассматривается круг, называются его признаки. Затем предъявляется квадрат и называется: «это квадрат». Дети сравнивают фигуры по цвету (одинаковые), размеру, форме (с углами и без углов), используя все обследовательские действия. Упражнения на закрепление.

Часто для повышения интереса и развития внимания используются стихотворные тексты, например:

Нет углов у меня, и похож на блюдце я,

На тарелку и на крышку, на кольцо, на колесо,

Кто же я такой, друзья? назовите вы меня?

Он давно знакомый мой, каждый угол в нем прямой,

Все четыре стороны одинаковой длины.

Вам его представить рад. Как зовут его? (…)

Колесо катилось. Вдруг ему навстречу вышел Круг:

«Ты, видать, моя родня, тоже круглый, как и я.

Сколько пальцем не веди, без углов выходим мы!

По дороге далеко нам катиться так легко!»

Тут навстречу им квадрат: «До чего ж друзьям я рад!

Покатился бы я с вами, да углы всегда мешали,

Их четыре у меня угловатых паренька,

Да четыре стороны все прямые, вот они.

И равны между собой, полюбуйся-ка любой!

Ну-ка пальцем проведи: есть преграды на пути.

Мне катиться не дано, зато ждет меня окно.

Нам дружить приятно, по всякому квадратно!»

III ЭТАП – 3-4 года.

Цель: познакомить с треугольником, выделяя его характерные особенности; продолжать учить сравнивать геометрические фигуры между собой.

Используются те же приемы работы. Необходимо учесть, что треугольник сравнивают и с кругом, и с квадратом, находя все признаки сходства и отличия. Кроме того, фигуры можно демонстрировать в разном пространственном положении для подведения к обобщению. Сериация, группировка, узоры, мозаика.

IV ЭТАП – 4-5 лет.

Цель: познакомить с прямоугольником, учить называть и различать круг, квадрат, треугольник и прямоугольник; дать представление о характерных признаках этих фигур (наличие углов, сторон, их количество, соотнесение по размеру).

· При знакомстве с прямоугольником необходимо помнить, что для различения этой фигуры ребенок должен владеть элементарным обобщением, т.к. квадрат то же является прямоугольником.

· Подбирая наглядный материал, учесть, что у прямоугольника длина должна быть в два раза больше ширины (на первых занятиях), длины сторон квадрата должны быть равны ширине прямоугольника. Это используется для выявления особенностей этих фигур.

· Постепенно от сравнения практическим путем переходить к сравнению на глаз.

· Сравнивая прямоугольник с другими фигурами, уточнить представления детей о квадрате и треугольнике: у них разное количество углов, побуждать детей к счету углов, сторон.

· Фигуры для сравнения предлагаются разного цвета, величины, изменяется соотношение сторон, чтобы создать предпосылки для обобщения на основе выделения существенных свойств – «все квадраты».

Фрагмент занятия: Незнайка приносит детям посылку и говорит:

- Сейчас мы будем играть: я буду доставать фигуры, а вы будете их отгадывать. (Достает круг).

- Что это? А как догадались?

- А теперь я отгадаю. (Достает треугольник). Это квадрат. Почему нет? А что это?

- А как эта фигура называется? (Достает квадрат).

- Ой, а этой фигуры я не знаю. (Достает прямоугольник). Может, это тоже квадрат?

Воспитатель:

- Нет, Незнайка, это не квадрат, хотя и очень похож на него. Это его старший брат – прямоугольник. Давайте на него внимательно посмотрим (выставить все фигуры перед детьми).

- У прямоугольника есть стороны (показать), углы (показать веером) и вершины (показать точкой); предложить то же самое сделать детям. Затем найти эти части у квадрата и треугольника. Так же дети работают с раздаточным материалом.

- Чем похож прямоугольник на квадрат? А на треугольник? Давайте их сосчитаем: сколько сторон? Углов? Вершин? У какой фигуры тоже 4 стороны, 4 угла и 4 вершины? Почему их можно назвать «братьями»?

- Чем отличается прямоугольник от квадрата? Давайте их приложим друг к другу. Что вы видите? (далее с помощью прикладывания, перегибания, использования эквивалента обобщить, что у квадрата все стороны равны, а у прямоугольника только по две равные стороны).

V ЭТАП – 5-6 лет.

Цель: познакомить с четырехугольником, дать общее представление о том, что у любого четырехугольника по 4 стороны, угла и вершины.

Фрагмент занятия: на фланелеграфе выставляется набор геометрических фигур:

· На какие группы можно разделить все фигуры? (с углами и без).

· Какая из оставшихся фигур лишняя и почему? (треугольник).

· Названия каких из оставшихся фигур вы знаете? (квадрат, прямоугольник).

· А как могут называться эти фигуры? Давайте придумаем вместе.

· Чем похожи все эти фигуры? (у них по 4 угла…).

· Почему треугольник так называется?

· Если у этих фигур по 4 угла, то, как их можно назвать?

· Покажите теперь все четырехугольники.

· Можно ли квадрат и прямоугольник назвать четырехугольниками? Почему?

В старшей группе для правильных обобщений геом. фигуры необходимо демонстрировать в разных положениях с варьированием несущественных признаков. При этом дети должны уметь выделить части геом. фигур, сравнить их по свойствам.

VI ЭТАП – 6-7 год жизни.

Цель: дать общее представление о многоугольнике, овале; учить различать границы многоугольника, внутреннюю и внешнюю области фигуры; познакомить с геом. телами: шар, куб, цилиндр, конус. Эта задача решается на основе рассматривания геом. фигур, анализа их строения, выделения существенных признаков. Понятие «многоугольник» вводится на основе обобщения: все фигуры, имеющие углы, называются многоугольниками.

Можно подойти к понятию «многоугольник» через понятие «точка». Для этого рассмотреть с детьми, как из точек получаются линии, которые могут быть кривыми (показать на модели провисшей ниточки), прямыми (нитку натянуть), найти эти линии в окружающей обстановке.

Далее продемонстрировать, как получается отрезок (вырезать часть нитки), показать, что его можно нарисовать, что палочка – это тоже модель отрезка.

Далее несколько отрезков прикладываются друг к другу таким образом, что конец одного отрезка служит началом другого – так получается ломаная линия.

Затем сравнить ломаную незамкнутую и ломаную замкнутую, уточнить, на что похожа замкнутая ломаная линия – это и есть многоугольник.

Многоугольники бывают разные : треугольник, четырехугольник, квадрат и т.д.. Упражнение «Разговор фигур: у меня больше углов» (стрелками).

Упражнения на геометрические преобразования

· С помощью штриховки и обведения выделить области фигуры и ее границу.

· Детям предлагается определить характер взаимного расположения фигур: какие фигуры находятся вне круга, внутри квадрата, за границей фигуры, справа;

· Какие фигуры могут получиться при пересечении квадрата и треугольника? И др. Сначала анализ на моделях, затем по представлению.

· Начерти фигуры так, чтобы областью пересечения был треугольник, чтобы круг был частью квадрата, чтобы фигуры не имели общих точек;

В старшей и подготовительной группах одно из направлений работы – преобразование разных геом. фигур двумя способами: разрезанием и складыванием. Данная работа в целом проводится уже со средней группы не только в процессе специальных занятий. Дети в играх с мозаикой осваивают принципы получения новых геометрических фигур путем складывания. Однако в этом случае знания детей носят стихийный характер и мало связаны с формированием геом. представлений.

В старшем возрасте данный вид работы приобретает особую значимость, поэтому упражнения необходимо предлагать в системе. Сначала необходимо уточнить и дополнить знания детей о способах получения новых фигур путем разрезания. Эта работа проводится в тесной связи с изучением отношений между частью и целым.

Типы заданий:

· деление геом. фигур на части указанной формы (перегибание, разрезание, линиями)

С этой целью можно прочитать стихотворение:

Давным-давно в темном лесу в фигурной избушке

Жили-были два брата, два квадрата.

И были они близнецами. Убедитесь сами:

Видите на картинке – у каждого 4 стороны, 4 угла и 4 вершинки.

Гулял как-то первый квадрат между кустами,

Стучал по дорожке четырьмя уголками.

А звери говорят: «Кто это? Первый квадрат или его брат, второй квадрат? Как же они похожи!

Помните на картинке: 4 стороны, 4 угла и 4 вершинки.

Надоело квадрату, что его путают с братом,

И решил он измениться, в другую фигуру превратиться.

Взял он ножницы и срезал себе четыре уголка.

В круг превратился и по дорожке покатился.

И живется теперь братьям чудно, перепутать теперь братьев трудно:

Один катается по дорожкам, другой ходит на четырех уголках - четырех ножках.

До сих пор дружат два брата – круг с квадратом.

· составление фигур из имеющихся по заданным условиям: из 2-х треугольников – квадрат, из 2-х квадратов – прямоугольник, из 2-х треугольников – треугольник и т.п.… Целесообразно предлагать самостоятельно определять, какие фигуры могут получиться из данного набора фигур. Для закрепления, систематизации знаний, развития устойчивых представлений о геом. фигурах и их свойствах, для развития геометрического и пространственного мышления необходимо: лепить геом. фигуры; выкладывать их из палочек; конструировать из проволоки; вырезать из бумаги; чертить, рисовать от руки и т.д.

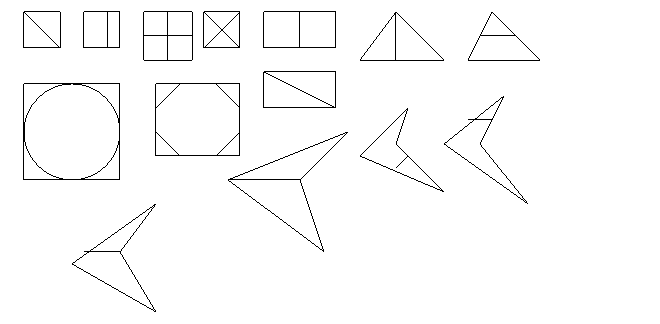
· распознавание геом. фигур на чертеже

- найти три треугольника и три четырехугольника

- сколько всего прямоугольников?

- сколько фигур и какие?

ЛОГИЧЕСКИЕ БЛОКИ ДЬЕНЕША

Ребенок познает окружающий мир предметов и явлений в их разнообразных отношениях и связях: учится устанавливать связи между частями одного предмета, между разными вещами и внутри целой картины мира. Эффективным средством формирования этих умений являются логико-математические игры, которые способствуют развитию не только ЭМП, но и логических структур мышления и умственных действий. Эти игры способствуют тому, что в игровой деятельности ребенок постепенно переходит от внешних практических действий с конкретными предметами к умственным действиям над свойствами предметов или отношениями между ними. В этих играх используется специфический структурированный дидактический материал, позволяющий наглядно представить абстрактные понятия отношения между ними: БЛОКИ, СХЕМЫ, СИМВОЛЫ СВОЙСТВ.

Организация познавательной деятельности детей происходит таким образом, что сообщается то, что надо сделать, а способ действия дети открывают самостоятельно.

В играх с блоками дети учатся:

ü сравнивать предметы на основе выделения их свойств, пользоваться логическими терминами "такой же", "не такой"

ü образовывать множества предметов на основе общего свойства, обобщать предметы с помощью терминов "все", "ни один", "каждый"

ü выделять часть множества (подмножество) и образовывать на этой основе частные и отрицательные суждения: "некоторые блоки желтые", "эти блоки не круглые"

ü находить пересечение и объединение множеств, пользуясь терминами "и", "или"

ü разбивать множество на классы

Комплект наглядного материала:

1. объемные блоки – 48 штук (4 формы, 3 цвета, 2 величины, 2 толщины)

2. плоские блоки – 24 штуки (4 формы, 3 цвета, 2 величины)

3. набор карточек – символов для обозначения свойств (наличие и отрицание)

4. наборы "жизненного материала"

5. схемы, таблицы для организации игр и упражнений

Для формирования у детей определенных логических структур используются три группы постепенно усложняющихся упражнений (Е.А.Носова. Логика и математика для дошкольников. – СПб, "Акцидент", 1996)

I. Для развития умения выявлять и абстрагировать свойства

II. Для развития умения сравнивать предметы по свойствам

III. Для развития способности к логическим действиям и операциям

Каждая группа представлена вариантами игр на развитие умения оперировать 1, 2 или 3(4) свойствами.

I II III I II III

Младший возраст Старший возраст

ПРИМЕРЫ ИГР С БЛОКАМИ

I группа: выявление и абстрагирование свойств	Найди клад. Поручения. Кто быстрее соберет? Мышки – норушки. Запасы на зиму. Автотрасса. Выращивание дерева. Необычные фигуры. Где чей гараж? Научи Незнайку. Загадки без слов. Переводчики. Сколько?
I I группа: сравнение, классификация, обобщение	Дорожки. Построй цепочку. Мост через речку. Поезд. Домино. Две дорожки. Второй ряд. У кого в гостях Винни-Пух и Пятачок? Покупки в магазине. Фабрика. Два правила. Дружат – не дружат. Угощения для медвежат. Архитекторы.
I I I группа: логические действия и операции	Помоги фигурам выбраться из леса. Найди выход. Готовим выставку. Оформим витрину. Построй дом. На свою веточку. Дерево. Муравьи. Раздели блоки – 1. Один обруч. Раздели блоки – 2. Помоги игрушке. Два обруча. Раздели блоки – 3. Подарки для трех поросят. Три обруча.

Описание игр с блоками

Группа упражнений	Название игры	Содержание игры	Примечание
Выявление и абстрагирование свойств	Найди клад	Выбирают блоки одной формы (8), под ними прячут "клад" (ведущий), дети, чтобы его найти, задают вопросы "Под желтым?" – нет и т.д.	Во второй серии берут 16 блоков (одного цвета), в вопросе называют два свойства. В третьей серии (24 блока, одинаковые по размеру или толщине), называют три свойства.
Поручения. Кто быстрее соберет?	Ведущий называет свойство блока (игрушки), а дети быстро их складывают в коробочку.	После освоения 1-го свойства, называют сразу 2, потом 3.
Мышки-норушки. Запасы на зиму.	Ведущий называет свойство, дети отбирают и прячут блоки (исчезает зрительная опора).	Так же по 2(3) свойствам. Другие названия: "Заселим домики", "Помоги муравьишкам"
Автотрасса	Дети строят гоночную трассу по определенным правилам, которые указаны в блок-схеме. При повторении упражнения правила меняются (по цвету, форме…).	При выполнении заданий с 2(3) свойствами изменять сюжет: дорожка ко дворцу Снежной Королевы, навести порядок в шкафу Человека Рассеянного и т.д.
Выращивание дерева. Необычные фигуры.	Простые фигуры превращаются в сложные, правила указаны в таблицах. Сначала выяснить, с какой фигуры начать. Если от фигуры стрелка не отходит, то ничего приставлять не надо.	Для игры необходимы палочки, которые будут имитировать ветки необычного дерева.
Где чей гараж?	Дети расставляют машины в гараже на основе одного свойства. Играют парами, деля набор блоков.	Для игры нужны схемы, которые усложняются в зависимости от количества свойств.
Сравнение, классификация, обобщение.	Дорожки. Построй цепочку. Мост через речку. Поезд.	Из блоков дети выкладывают дорожки, н-р между домиками трех поросят. Правила дорожек меняются: рядом не должно быть фигур одного цвета (формы, размера…)	Дети учатся отрицать свойства: фигуры должны быть одинаковой формы и разного цвета и т.п.. так же по трем (4) свойствам.
Домино.	Играют 4 человека. Фигуры делят поровну. Договариваются о правилах, н-р, делать ход другим цветом.	Подбор правил тот же, что и в предыдущей игре.
Поймай пару.	Играют 5-7 человек. Один набор блоков у ведущего, второй делят поровну. Ведущий кладет любую фигуру, игроки должны найти ей пару – положить рядом фигуру, похожую по какому-либо свойству. Если правильно, то фигуру забрать себе, если нет, ее берет ведущий.	Во второй серии пара составляется по 2-м свойствам, затем по трем.
Две дорожки. Второй ряд.	В первой серии 2 игрока берут по 5 фигур, выкладывают стопкой. Первый игрок выкладывает в ряд все свои фигуры, начиная с верхней. Второй кладет рядом свои, если найдет общее свойство, забирает себе. В игре "Второй ряд" ведущий выкладывает некоторое кол-во фигур, задает правило, игрок строит второй ряд, за ошибку – штрафное очко.	Во второй серии – по 10 фигур, в 3-й по 12. Фигуры могут быть похожи по 2(3) свойствам, это обговаривается заранее.
Поймай тройку.	Ведущий складывает фигуры стопкой, снимает 2 верхние, кладет рядом. Первый игрок снимает следующую, кладет рядом и ищет общее свойство. Если правильно, забирает себе, если нет, то кладет вниз стопки.	Если общее свойство обнаруживает другой игрок, то он забирает. Выигрывает тот, кто соберет больше фигур.
У кого в гостях Вини-