III. Тесты по теории вероятностей.

Каждый из предлагаемых тестов имеет один из двух возможных ответов: «да» или «нет».

Проверьте свои знания теории вероятностей перед экзаменом.

1. Если случайное событие B влечёт за собой случайное событие A, то .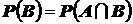

2. Любая дискретная случайная величина может принимать лишь конечное число значений.

3. Закон редких событий Пуассона является предельным случаем закона распределения Я.Бернулли.

4. Если при 500 опытах событие A произошло 11 раз, то можно утверждать, что A есть случайное событие.

5. Несовместные события – это то же самое, что и независимые события.

6. Нормальный закон Гаусса описывает поведение дискретной случайной величины.

7. Значение дисперсии 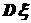любой случайной величины удовлетворяет условию .

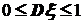8. Выигрыш по лотерейному билету является непрерывной случайной величиной.

9. В полной группе случайных событий все события всегда равновозможные.

10. Если 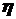- центрированная случайная величина, то .

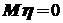11. Математическое ожидание любой случайной величины – это тоже случайная величина.

12. Если новую монету бросить 100 раз на пол, то она может все сто раз упасть гербом вверх.

13. Если монета – старая, то упасть подряд сто раз гербом вверх она не сможет.

14. Из совместности событий следует, что .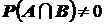

15. Если к случайной величине 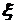прибавить число 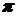, то дисперсия этой новой случайной величины 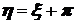будет такой же, как и дисперсия случайной величины .

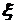16. Суммой двух случайных событий называют появление обоих этих случайных событий в одном испытании.

17. .

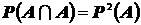18. .

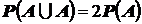19. ø 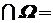ø.

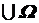20. P(ø )=1.

21. Коэффициент линейной корреляции безразмерен.

22. Если 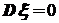, то и .

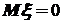23. Все события в полной группе случайных событий всегда несовместны.

24. В законе распределения вероятностей Бернулли всегда .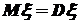

25. Функция Лапласа симметрична относительно оси ординат.

26. Несовместные случайные события всегда противоположны.

27. У некоторых случайных величин все их значения меньше их .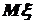

28. В каком случае произведение двух случайных событий будет совпадать с их суммой?

29. .

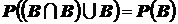30. .

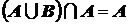31. Есть такие случайные величины, у которых ?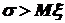

32. Если 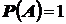, то .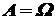

33. Если 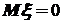, то и .

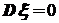34. «Лестница» гистограммы может идти то вверх, то вниз.

35. Коэффициент линейной корреляции 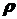иногда бывает <0.

36. Выборка – это подмножество элементов генеральной совокупности.

37. Плотность распределения непрерывной случайной величины всегда монотонна.

38. Биномиальный закон распределения – это частный случай закона Пуассона.

39. У некоторых случайных величин все их значения меньше их среднего квадратического отклонения .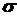

40. Закон Пуассона – это частный случай биномиального закона.

41. В формуле 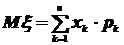число n –эточисло проведённых испытаний.

42. Противоположные случайные события всегда несовместны.

43. Существуют три разных противоположных друг другу случайных события.

44. Верно ли равенство: ?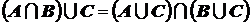

45. Всегда ли равенство: ?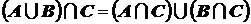

46. Дисперсия числа π равна нулю.

47. Относительная частота всегда безразмерна.

48. .

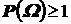49. Дисперсия является случайной величиной.

50. Среднее значение случайной величины всегда положительно.

51. Среднее значение случайной величины является случайной величиной.

52. Функция Лапласа всегда положительна.

53. Функция Лапласа – нечётная функция.

54. Для любого случайного события A всегда будет справедливо .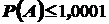

55. Из независимости событий следует их несовместность.

56. Из несовместности событий следует их независимость.

57. Если два события зависимые, то условная вероятность любого из них будет меньше его безусловной вероятности.

58. Если где-то во Вселенной есть высокоразвитые цивилизации, то развитие математики у них непременно приведёт к созданию Теории Вероятностей?

IV. Экзаменационные вопросы

В каждом экзаменационном билете содержатся названия терминов и понятий теории вероятностей, которым надо дать определения, и два теоретических вопроса. Первый вопрос билета призван проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях.

1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами.

2. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: повторные независимые испытания.

3. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания до первого положительного исхода.

4. Условная вероятность. Вероятность произведения событий. Зависимые и независимые события.

5. Формула полной вероятности.

6. Формула Байеса.

7. Аксиоматическое построение вероятностной модели. Аксиомы А.Н. Колмогорова.

8. Свойства 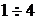вероятностной функции.

9. Теорема о непрерывности вероятностной функции. Импликаци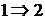и и .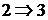

10. Теорема о непрерывности вероятностной функции. Импликаци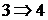и и .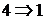

11. Измеримое пространство <R,B(R)>. Борелевские множества на множестве вещественных чисел.

12. Измеримое пространство <Rⁿ,B(Rⁿ)>. Борелевские множества на плоскости.

13. Вероятностная функция дискретного типа на измеримых пространствах <R,B(R)> и <Rⁿ,B(Rⁿ)>. Примеры.

14. Вероятностная функция непрерывного типа на измеримых пространствах <R,B(R)> и <Rⁿ,B(Rⁿ)>. Примеры.

15. Случайная величина. Типы случайных величин. Функция распределения случайной величины.

16. Случайный вектор. Компоненты случайного вектора. Частные вероятностные функции и частные функции распределения.

17. Функция распределения. Свойства. Примеры функций распределения дискретного типа.

18. Функция распределения. Свойства. Примеры функций распределения непрерывного типа.

19. Многомерная функция распределения. Свойства. Примеры. Свойства согласованности.

20. Независимость компонент случайного вектора. Критерий независимости.

21. Математическое ожидание случайной величины. Определение. Примеры.

22. Математическое ожидание случайной величины. Определение. Свойства.

23. Дисперсия случайной величины. Определение. Примеры.

24. Дисперсия случайной величины. Определение. Свойства.

25. Функции случайных величин. Определение закона распределения функции случайной величины. Примеры.

26. Функция распределения суммы двух независимых случайных величин. Свёртка функций распределения.

27. Начальные и центральные моменты случайной величины.

28. Числовые характеристики случайного вектора. Ковариационный момент. Ковариационная матрица.

29. Коэффициент линейной корреляции. Определение. Свойства.

30. Характеристические функции. Определение Примеры.

31. Характеристические функции. Свойства .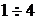

32. Характеристические функции. Свойства .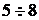

33. Закон больших чисел. Теорема Бернулли и теорема А.Я. Хинчина. Правило среднего арифметического.

34. Закон больших чисел. Неравенство и теорема П.Л. Чебышёва.

35. Центральная предельная теорема. Теорема Муавра-Лапласа.

36. Центральная предельная теорема. Теорема Леви. Следствия.

37. Центральная предельная теорема. Понятия о теоремах А.М. Ляпунова и Линдебега-Феллера.

38. Закон малых чисел. Теорема Пуассона.

39. Выборка. Первичная обработка статистических данных. Теорема Гливенко.

40. Точечные оценки числовых характеристик случайных величин. Требования к точечным оценкам.

41. Неравенство Рао-Крамера. Эффективность оценки математического ожидания - среднего арифметического элементов выборки.

42. Метод моментов получения точечных оценок числовых характеристик случайных величин.

43. Метод максимального правдоподобия получения точечных оценок числовых характеристик случайных величин.

44. Некоторые специальные распределения, используемые в математической статистике.

45. Интервальные оценки числовых характеристик случайных величин. Доверительный интервал для математического ожидания.

46. Интервальные оценки числовых характеристик случайных величин. Доверительный интервал для дисперсии.

47. Статистическая проверка гипотез. Ошибки первого и второго рода. Три типа задач статистической проверки гипотез.

48. Статистическая проверка гипотезы о равенстве математического ожидания некоторому фиксированному числу.

49. Статистическая проверка гипотезы о равенстве дисперсии некоторому фиксированному числу.

50. Статистическая проверка гипотезы о равенстве дисперсий двух различных случайных величин.

51. Статистическая проверка гипотезы о равенстве математических ожиданий двух различных случайных величин.

52. Статистическая проверка гипотез. Понятия о критериях Колмогорова и Мизеса.

53. Статистическая проверка гипотезы о виде закона распределения случайной величины. Критерий согласия Пирсона.

54. Элементы корреляционного и дисперсионного анализов. Две задачи корреляционного анализа. Статистическая оценка коэффициента линейной корреляции.

55. Условные распределения и условные математические ожидания. Определение функции регрессии.

56. Статистическая оценка коэффициентов линейной функции регрессии методом наименьших квадратов.

57. Остаточная дисперсия при линейной регрессии.

58. Корреляционное отношение – мера силы статистической связи при нелинейной регрессии.

7. Учебно-методическое и информационное обеспечение дисциплины

а) основная литература:

1. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983.

2. Боровков А.А. Курс теории вероятностей. - М.: Наука, 1986.

3. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1973.

4. Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей. – М.: Высшая школа, 2000.

5. Гнеденко Б.В. Курс теории вероятностей. - М.: Наука, 1988.

6. Драгилев М.М. Теория вероятностей. – М.: Вузовская книга, 2002.

7. Кожевников Ю.В. Теория вероятностей и математическая статистика. – М.: Машиностроение, 2002.

8. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1991.

9. Крамер Г. Математические методы статистики. - М.: Мир, 1975.

10.В.Е. Ковальчук, А.И. Луценко Индивидуальные задания по математической статистике, УПЛ РГУ, 1999.

11.А.И. Луценко Теория вероятностей, ЮФУ, 2009.

12.А.И. Луценко Задачи по теории вероятностей. Часть I, УПЛ РГУ,2005А.И. Луценко Задачи по теории вероятностей. Часть II УПЛ РГУ, 2000. университета, 1963.

13.Сборник задач по теории вероятностей, математической статистике и теории случайных функций, под редакцией Свешникова А.А. – М.:Наука, 1970.

14.Севастьянов Б.А., Курс теории вероятностей и математической статистики. – М.; Наука, 1982.

15.Севастьянов Б.А., Чистяков В.П., Зубков Ф.М. Сборник задач по теории вероятностей. - М.: Наука, 1980.

16.Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. - М.: Физматгиз, 1980.

17.Феллер В. Введение в теорию вероятностей и ее приложения. В 2-х томах - М.: Мир, 1984.

18.Чистяков В.П. Курс теории вероятностей. - М.: Наука, 1982.

19.Ширяев А.Н. Вероятность. – М.: Наука, 1980.

Материалы к дисциплине размещены на ресурсе http://www.math.rsu.ru/mexmat/; студентам предлагается искать дополнительную информацию на сайтах, посвященных теории вероятностей, математической статистике и теории случайных процессов.

8. Материально-техническое обеспечение дисциплины

Наличие литературы в отраслевой библиотеке, медиапроектор и компьютер для проведения лекций-презентаций.

Программа составлена в соответствии с требованиями ФГОС ВПО с учетом рекомендаций и ПрООП ВПО по направлению и профилю подготовки ____________________ .

Автор _Луценко А.И.

Рецензент _________________________

Программа одобрена на заседании кафедры ТФиФА ______________________протокол №_____________________

(Наименование уполномоченного органа вуза (УМК, НМС, Ученый совет)

от ___________ года, протокол № ________.