Поиск нескольких минимумов на отрезке. Задача поиска подстрок. Алгоритм Рабина-Карпа. Конечный автомат. Алгоритм Бойера-Мура.

Поиск нескольких минимумов на отрезке.

0.Если требуется получать сразу несколько минимумов по отрезку (всегда nминимумов на отрезке) – делаем дерево отрезков с функцией нахождения этих нескольких минимумов (но придется делать kсравнений èв kраз усложняет время)

1.Альтернатива

Надо найти kминимумов. Находим по RMQ – индекс первого. Потом запускаем RMQна подмассивах, на которые делится наш массив найденным индексом. Так найдем уже 3 минимума. И т.д. (на 4 подмассивах и т.д.)

Поиск подстроки в строке.

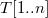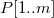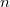
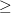
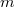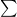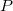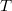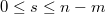Имеются строки и такие, что и элементы этих строк символы из конечного алфавита . Говорят, что строка встречается в строке со сдвигом , если и 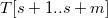= 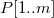. Если строка 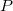встречается в строке 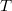, то 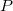является подстрокой 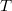. Требуется проверить, является ли строка 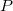подстрокой .

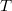В задачах поиска традиционно принято обозначать шаблон поиска как needle а строку, в которой ведётся поиск — как haystack . Также обозначим через Σ алфавит, на котором проводится поиск.

Если считать, что строки нумеруются с 1, простейший алгоритм (англ. brute force algorithm, naïve algorigthm) выглядиттак.

for i=0...|haystack|-|needle|for j=1...|needle|if haystack[i+j]<>needle[j] then goto 1output("Найдено: ", i+1)1:

Простейший алгоритм поиска даже в лучшем случае проводит |haystack|−|needle|+1 сравнение; если же есть много частичных совпадений, скорость снижается до O(|haystack|·|needle|).

Показано, что примитивный алгоритм отрабатывает в среднем 2h сравнений

Метод хеширования

Для решения задачи удобно использовать полиномиальный хеш, так его легко пересчитывать: 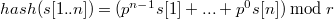, где 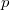— это некоторое простое число, а — некоторое большое число, для уменьшения числа коллизий (обычно берётся 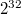или 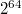, чтобы модуль брался автоматически при переполнении типов). Стоит обратить внимание, что если 2 строчки имеют одинаковый хэш, то они в большинстве таких случаев равны.

При удалении первого символа строки и добавлении символа в конец считать хеш новой строки при помощи хеша изначальной строки возможно за :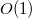

.

.

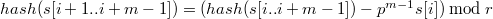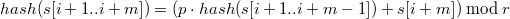Получается : .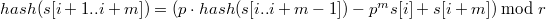

Следует учесть, что при получении отрицательного значения необходимо прибавить .

Алгоритм

Алгоритм начинается с подсчета 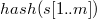и .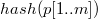

Для 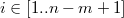вычисляется 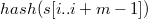и сравнивается с 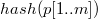. Если они оказались равны, то образец 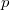содержится содержится в строке , начиная с позиции , но в этом случае возможны ложные срабатывания алгоритма. Если требуется свести такие срабатывания к минимуму или исключить вообще, то применяют сравнение некоторых символов из этих строк, которые выбраны случайным образом, или применяют явное сравнение строк, как в наивном алгоритме поиска подстроки в строке. В первом случае проверка произойдет быстрее, но вероятность ложного срабатывания останется хоть и небольшая, во втором случае проверка займет время равное длине образца, но исключит возможность ложного срабатывания.

Для ускорения работы алгоритма оптимально предпосчитать .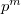

Если шаблон большой, нет большого увеличения по времени. Каждый шаг цикла не зависит от остальных (распараллеливание)

Время работы

Изначальный подсчёт хешей выполняется за 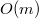. В цикле всего 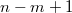итераций, каждая выполняется за 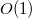. Итоговое время работы алгоритма .

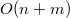RabinKarp (s[1..n], p[1..m])

hp = hash(p[1..m])

h = hash(s[1..m])

for i = 1 to n - m + 1

if h == hp

answer.add(i)

h = (p * h - p 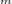* hash(s[i]) + hash(s[i + m])) mod r

if h < 0

h += r

if answer.size() == 0

return not found

Else

returnanswer

Конечный автомат — абстрактный автомат без выходного потока, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию.

Существуют различные варианты задания конечного автомата. Например, конечный автомат может быть задан с помощью пяти параметров: 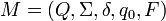, где:

· Q — множество состояний автомата;

· q₀ — начальное (стартовое) состояние автомата ( );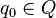

· F — множество заключительных (или допускающих) состояний, таких что ;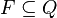

· Σ — допустимый входной алфавит (конечное множество допустимых входных символов), из которого формируются строки, считываемые автоматом;

· δ — заданное отображение множества 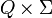во множество 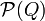подмножеств Q:

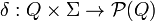
(иногда δ называют функцией переходов автомата).

Автомат начинает работу в состоянии q₀, считывая по одному символу входной строки. Считанный символ переводит автомат в новое состояние из Q в соответствии с функцией переходов. Если по завершении считывания входного слова (цепочки символов) автомат оказывается в одном из допускающих состояний, то слово «принимается» автоматом. В этом случае говорят, что оно принадлежит языку данного автомата. В противном случае слово «отвергается».

Через конечный автомат работают Ахо-Корасик, Бойер-Мур и Укконенн

Алгоритм Бойера-Мура

1. Сканирование слева направо, сравнение справа налево. Совмещается начало текста (строки) и шаблона, проверка начинается с последнего символа шаблона. Если символы совпадают, производится сравнение предпоследнего символа шаблона и т. д. Если все символы шаблона совпали с наложенными символами строки, значит, подстрока найдена, и поиск окончен.

Если же какой-то символ шаблона не совпадает с соответствующим символом строки, шаблон сдвигается на несколько символов вправо, и проверка снова начинается с последнего символа.

Эти «несколько», упомянутые в предыдущем абзаце, вычисляются по двум эвристикам.

2. Эвристика стоп-символа. Предположим, что мы производим поиск слова «колокол». Первая же буква не совпала — «к» (назовём эту букву стоп-символом). Тогда можно сдвинуть шаблон вправо до последней буквы «к».

!Строка: * * * * * * к * * * * * *Шаблон: к о л о к о лСледующий шаг: к о л о к о л

Если стоп-символа в шаблоне вообще нет, шаблон смещается за этот стоп-символ.

!Строка: * * * * * а л * * * * * * * *Шаблон: к о л о к о лСледующий шаг: к о л о к о л

В данном случае стоп-символ — «а», и шаблон сдвигается так, чтобы он оказался прямо за этой буквой. В алгоритме Бойера-Мура эвристика стоп-символа вообще не смотрит на совпавший суффикс (см. ниже), так что первая буква шаблона («к») окажется под «л», и будет проведена одна заведомо холостая проверка.

Если стоп-символ «к» оказался за другой буквой «к», эвристика стоп-символа не работает.

!Строка: * * * * к к о л * * * * *Шаблон: к о л о к о лСледующий шаг: к о л о к о л ?????

В таких ситуациях выручает третья идея АБМ — эвристика совпавшего суффикса.

3. Эвристика совпавшего суффикса. Если при сравнении строки и шаблона совпало один или больше символов, шаблон сдвигается в зависимости от того, какой суффикс совпал.

Строка: * * т о к о л * * * * *Шаблон: к о л о к о лСледующий шаг: к о л о к о л

В данном случае совпал суффикс «окол», и шаблон сдвигается вправо до ближайшего «окол». Если подстроки «окол» в шаблоне больше нет, но он начинается на «кол», сдвигается до «кол», и т. д.

Обе эвристики требуют предварительных вычислений — в зависимости от шаблона поиска заполняются две таблицы. Таблица стоп-символов по размеру соответствует алфавиту (например, если алфавит состоит из 256 символов, то её длина 256); таблица суффиксов — искомому шаблону. Именно из-за этого алгоритм Бойера-Мура не учитывает совпавший суффикс и несовпавший символ одновременно — это потребовало бы слишком много предварительных вычислений.

Опишем подробнее обе таблицы.

Таблица стоп-символов

В таблице стоп-символов указывается последняя позиция в needle (исключая последнюю букву) каждого из символов алфавита. Для всех символов, не вошедших в needle, пишем 0 (для нумерации с 0 — соответственно, −1). Например, если needle=«abcdadcd», таблица стоп-символов будет выглядеть так.

Символ a b c d [все остальные]Последняя позиция 5 2 7 6 0

Обратите внимание, для стоп-символа «d» последняя позиция будет 6, а не 8 — последняя буква не учитывается. Это известная ошибка, приводящая к неоптимальности. Для АБМ она не фатальна («вытягивает» эвристика суффикса), но фатальна для упрощённой версии АБМ — алгоритма Хорспула.

Если несовпадение произошло на позиции i, а стоп-символ c, то сдвиг будет i-StopTable[c].

Таблица суффиксов

Для каждого возможного суффикса S шаблона needle указываем наименьшую величину, на которую нужно сдвинуть вправо шаблон, чтобы он снова совпал с S. Если такой сдвиг невозможен, ставится |needle| (в обеих системах нумерации). Например, для того же needle=«abcdadcd» будет:

Суффикс [пустой] d cd dcd ... abcdadcdСдвиг 1 2 4 8 ... 8Иллюстрация было ? ?d ?cd ?dcd ... abcdadcd стало abcdadcd abcdadcd abcdadcd abcdadcd ... abcdadcd

Если шаблон начинается и заканчивается одной и той же комбинацией букв, |needle| вообще не появится в таблице. Например, для needle=«колокол» для всех суффиксов (кроме, естественно, пустого) сдвиг будет равен 4.

Суффикс [пустой] л ол ... олокол колоколСдвиг 1 4 4 ... 4 4Иллюстрация было ? ?л ?ол ... ?олокол колокол стало колокол колокол колокол ... колокол колокол

Существует быстрый алгоритм вычисления таблицы суффиксов. Этот алгоритм использует префикс-функцию строки.

m = length(needle)pi[] = префикс-функция(needle)pi1[] = префикс-функция(обращение(needle))for j=0..msuffshift[j] = m - pi[m]for i=1..m j = m - pi1[i]suffshift[j] = min(suffshift[j], i - pi1[i])

Здесь suffshift[0] соответствует всей совпавшей строке; suffshift[m] — пустому суффиксу. Поскольку префикс-функция вычисляется за O(|needle|) операций, вычислительная сложность этого шага также равняется O(|needle|).

Поиск со звездочками. Алгоритм Кнута-Морриса-Пратта.

Поиск со зведочками

Дан шаблон со звездочками (* - любой символ, но только 1), например ab*av**a (слово abqavqqa - подходит)

Как осуществлять поиск? Надо разбить шаблон на шаблоны без звезд (назовем массив таких шаблонов - runs). То есть в вышеописанном примере runs = {ab,av,a}. Кроме того будем хранить позицию начала этих шаблонов (без *) во всем шаблоне.

Создадим массив counts длины нашего текста. Изначально элементы равны в нем 0.

Затем запустим поиск в тексте всех шаблонов без * (из массива runs). Это будет происходить по очереди, если используем КМП, или сразу, если Ахо-Корасик. Затем будем делать counts[entry - runs[j].position]++, если j-ый шаблон из массива runs встретился в нашей строке на позиции entry

Потом мы пройдемся по массиву counts и все позиции в нем, где значение равно количеству шаблонов без * - это вхождения нашего шаблона (всего)